Реферат: Определение точного коэффициента электропроводности из точного решения кинетического уравнения

В.Кинетические Свойства

§ 6. Кинетическое уравнение

Носители заряда в металле или полупроводнике могут подвергаться действию внешних полей и градиентов температуры. Они также испытывают рассеяние на примесях, колебаниях решетки и т. д. Эти эффекты должны быть сбалансированы — нас интересуют такие ситуации, в которых электрон ускоряется полем, но при рассеянии теряет избыточные энергию и импульс. В этой главе мы рассмотрим «обычные» кинетические свойства, наблюдаемые при наложении постоянных полей.

Общий метод решения этой задачи основан на кинетическом уравнении, или уравнении Болъцмана. Мы рассматриваем функцию fk(r) — локальную концентрацию носителей заряда в состоянии k в окрестности точки r. Строго говоря, эту величину можно определить только в терминах мелкозернистых распределений, средних по ансамблю, матриц плотности и т. д. Имеется обширная литература по этому вопросу, но она относится скорее к формальному аппарату квантовой статистической механики, чем к теории твердого тела.

Посмотрим теперь, какими способами функция fk(r) может изменяться во времени. Возможны процессы трех типов:

1. Носители заряда приходят в область пространства вблизи точки r и уходят из нее. Пусть vk — скорость носителя в состоянии k. Тогда в течение интервала времени t носители заряда в этом состоянии пройдут путь tvk. Следовательно, на основании теоремы Лиувилля об инвариантности фазового объема системы число носителей в окрестности точки r в момент времени t равно числу их в окрестности точки r – tvk в момент времени 0:

fk(r, t) = fk(r – tvk, 0). (35)

Это означает, что скорость изменения функции распределения из-за диффузии есть

¶fk/¶t]diff = – vk×¶fk/¶r = – vk×Ñfk. (36)

2. Внешние поля вызывают изменение волнового вектора k каждого носителя, согласно равенству

(37)

Величину можно рассматривать как «скорость» носителя заряда в k-пространстве, так что по аналогии с равенством (35) имеем

(38)

следовательно, под действием полей функция распределения меняется со скоростью

(39)

(мы использовали здесь обозначение ¶fk/¶k для градиента в k-пространстве — оператора Ñk).

3. Влияние процессов рассеяния оказывается более сложным. Мы ограничимся здесь в основном упругим рассеянием. При этом функция fk меняется со скоростью

¶fk/¶t]scatt = ∫{ fk' (1 – fk) – fk (l – fk')}Q(k, k') dk'. (40)

Процесс рассеяния из состояния k в состояние k' приводит к уменьшению fk. Вероятность этого процесса зависит от величины fk — числа носителей в состоянии k, и от разности (1 – fk') — числа свободных мест в конечном состоянии. Имеется также обратный процесс, переход из k' в k, который ведет к увеличению функции fk; он пропорционален величине fk'(1 – fk). Очевидно, надо просуммировать по всевозможным состояниям k'. Для каждой пары значений k и k' существует, однако, «собственная» вероятность перехода Q (k, k'), равная скорости перехода в случае, когда состояние k полностью заполнено, а состояние k' вакантно. Согласно принципу микроскопической обратимости, та же функция дает и скорость перехода из k' в k, поэтому под интегралом появляется общий множитель.

Кинетическое уравнение выражает следующее: для любой точки r и для любого значения k полная скорость изменения функции fk(r) равна нулю, т. е.

¶fk/¶t]scatt + ¶fk/¶t]field + ¶fk/¶t]diff = 0. (41)

Отметим, что здесь рассматривается стационарное, но не обязательно равновесное состояние. Для последнего функция распределения обозначается через f0k, оно осуществляется только в отсутствие полей и градиентов температуры.

Допустим, однако, что рассматриваемое стационарное распределение не слишком сильно отличается от равновесного.
Положим

gk = fk – f0k. (42)

где

f0k = 1/{exp[(E k – z)/kT] + 1} (43)

Здесь нужно проявить некоторую осторожность. Именно, как определить функцию f0k в случае, когда температура зависит от координат? Будем считать, что в каждой точке можно корректно определить локальную температуру T(r), и положим

gk(r)=fk(r) – f0k{3T(r)}. (44)

Если введение локальной температуры вызывает затруднения, можно потребовать, чтобы окончательное решение удовлетворяло какому-либо дополнительному условию, например

ògk(r)dk = 0. (45)

Подставляя выражение (42) в кинетическое уравнение (41) и используя равенства (7.2) и (7.5), получаем

– vk×¶fk /¶r – e /ħ(E + 1/c[vk ´ H]) ×¶fk /¶k = – ¶fk /¶t]scatt , (46)

или

– vk×¶fk /¶T ÑT – e /ħ(E + 1/c[vk ´ H]) ×¶ f0k /¶k = – ¶fk /¶t]scatt + vk×¶gk /¶r + e /ħ(E + 1/c[vk ´ H]) ×¶gk /¶k. (47)

С помощью формулы (43) это уравнение можно переписать в виде

(¶f0 /¶E)vk×{( E (k) – z) / T×ÑT + e (E – 1/e×Ñz)} = – ¶fk /¶t]scatt + vk×¶gk /¶r + e /ħc[vk ´ H] ×¶gk /¶k. (48)

Это — линеаризованное уравнение Больцмана. В нем опущен член (E×¶gk /¶k) порядка E2, соответствующий отклонениям от закона Ома. Отброшен также член vk [vk ´ H], тождественно равный нулю; в левую часть уравнения магнитное поле явно не входит.

Подставляя выражение (40) в уравнение (48), можно убедиться, что мы получили линейное интегро-дифференциальное уравнение относительно «добавки» gk(r) к функции распределения. Функция gk(r) определяется интенсивностью электрического поля и величиной градиента температуры, входящими
в неоднородный член в левой части. Далее в этой главе мы будем отыскивать решения кинетического уравнения для различных случаев в порядке увеличения сложности.

§ 7. Электропроводность

Пусть на систему наложено только электрическое поле E, и в «бесконечной» среде поддерживается постоянная температура. С учетом выражения (40) получаем

(– ¶f0 /¶E)vk×eE = – (¶f0 /¶t)]scatt = ò(fk– fk¢)Q(k,k¢)dk¢= ò(gk– gk¢)Q(k,k¢)dk¢ (49)

Это есть простое интегральное уравнение для неизвестной функции gk.

Вместо того чтобы, непосредственно решать его, сделаем феноменологическое предположение:

– ¶fk /¶t]scatt = gk/t (50)

Тем самым мы вводим время релаксации t. При выключении поля любое отклонение gk от равновесного распределения будет затухать по закону

– ¶gk /¶t = gk/t, (51)

или

gk(t) = gk(0)e – t / t . (52)

Подставляя определение (50) в уравнение (49), находим

gk = (– ¶f0 /¶E) tvk×eE (53)

Чтобы найти электропроводность, вычислим соответствующую плотность тока

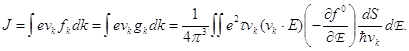(54)

Здесь при переходе от первой строки ко второй принято во внимание, что

òf0kevk(r)dk º 0,

использованы также формулы для преобразования объемного интеграла в k-пространстве в интеграл по изоэнергетическим поверхностям и по энергии.

В металле функция (– ¶f0 /¶E) ведет себя как d-функция от (E – z), поэтому остается только проинтегрировать по поверхности Ферми. Таким образом,

(55)

Сравним это выражение с обычной макроскопической формулой

J = s×E, (56)

где s – тензор. Получим

(57)

Обычно имеют дело с кристаллами кубической симметрии,при этом тензор электропроводности сводится к скаляру, помноженному на единичный тензор. В случае, когда оба вектора E и J направлены по оси х, подынтегральное выражение в (55) есть

(vk vk × E) = v2xE, (58)

что дает 1/3 вклада от квадрата скорости, v2E. Поэтому

(59)

где мы ввели длину свободного пробега

L = tv. (60)

Это есть основная формула для электропроводности.

Интересно посмотреть (фиг. 97), как выглядит функция распределения fk, заданная выражением (7.8). Как видно из равенства (53), функция gk велика только вблизи поверхности Ферми.

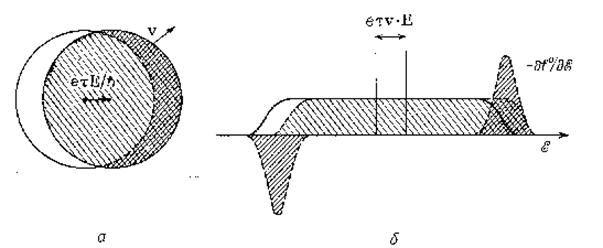
Фиг.97. а – смещенная поверхность Ферми; б – смещенное распределение Ферми.

Небольшая добавка появляется с той стороны, где vk×eE>0, т. е. там, где электроны ускоряются полем. Та же величина вычитается с противоположной стороны.

Фактически по теореме Тейлора можно написать

(61)

Это выглядит так, как будто вся сфера Ферми сдвинулась в k-пpoстранстве на величину (et/ħ)E. Это несколько неверная интерпретация. В действительности поле не действует на состояния вблизи дна зоны, в глубине сферы Ферми. Из-за принципа Паули поле не может придать ускорения электронам в таких состояниях; по этой же причине они не рассеиваются примесью.

Отметим, однако, что электропроводность не зависит от температуры (если не считать возможной температурной зависимости t). Эта же формула справедлива при T = 0, когда распределение Ферми имеет совершенно четкую границу. Можно сказать, что электропроводность выражается через смещение жесткой поверхности Ферми.

Заметим также, что выражение (61) можно представить в виде

fk = f0(Ek + etvkE), (62)

как будто к энергии электрона в состоянии k добавилась величина

dEk = etvkE. (63)

Это в точности соответствует классической ситуации, которая имела бы место, если бы электрон со скоростью vk двигался в поле E в течение интервала времени t. Это замечание лежит в основе кинетического метода решения подобных задач. Добавочная энергия, приобретаемая в промежутках между столкновениями с примесями, соответствует наличию дрейфовой скорости dv в направлении поля; именно

dv(¶E/¶v) = evEt, (64)

или для классической частицы массы m

dv(¶E/¶v) = evEt / mv. (65)

Пусть концентрация частиц есть n, тогда полная плотность тока равна

J = nedv, (66)

и, сравнивая формулы (65), (66) и (56), находим

s = ne2t/m. (7.33)

Легко показать, что в случае свободного электронного газа формулы (67) и (59) эквивалентны; в металле последняя формула принципиально значительно лучше. Она показывает, что электропроводность зависит только от свойств электронов на уровне Ферми, а не от полной концентрации их. Большую электропроводность металлов следует объяснять скорее наличием небольшой группы очень быстрых электронов на вершине распределения Ферми, а не высоким значением полной концентрации свободных электронов, которым можно придать небольшую дрейфовую скорость.

Основная формула (59) показывает также, что происходит, когда площадь свободной поверхности Ферми уменьшается в результате взаимодействия с границами зоны, и учитывает влияние решетки, ограничивающее эффективную скорость электронов на поверхности Ферми. Такие эффекты действительно можно наблюдать в металлах типа Bi.

С другой стороны, формула кинетической теории (67) удобна для полупроводников. При этом под п следует понимать концентрацию свободных носителей заряда. Обычно пишут

s = n|е|m (68)

где

m = |e|t/m (69)

есть подвижность носителей. В более общем случае считают, что электроны и дырки вносят независимые вклады в полный ток и определяют их подвижности равенством

s = nh |е| mh + ne |е| me . (70)

Нетрудно вывести формулу (68), скажем, из (54), принимая в качестве f° классическую функцию распределения. При этом мы допускаем, что время релаксации t может зависеть от энергии; в формулу (69) надо подставить его среднее значение

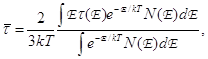(71)

где N(E) есть плотность состояний в рассматриваемой зоне. Таким образом,

me= |e|te /me (7.38)

где те — эффективная масса электронов. Аналогичная формула справедлива и для дырок. Из этих формул видно, что подвижность может зависеть от температуры. С ростом T распределение размазывается и среднее время релаксации изменяется. В случае металла то обстоятельство, что т зависит от энергии, не играет большой роли, ибо существенно только значение t (EF).