Реферат: Исследование эмпирической зависимости

Реферат: Исследование эмпирической зависимости

ГОСУДАРСТВЕННЫЙ КОМИТЕТ

РОССИЙСКОЙ ФЕДЕРАЦИИ ПО ВЫСШЕМУ

ОБРАЗОВАНИЮ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ

ИНСТИТУТ РАДИОТЕХНИКИ, ЭЛЕКТРОНИКИ

И АВТОМАТИКИ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

КУРСОВАЯ РАБОТА

ТЕМА: «Исследование эмпирической зависимости».

КУРС: «Математическое моделирование экономических процессов».

Студентки группы МФ-3-95

Франковской К. И.

____________________________________________________________________________МОСКВА 1998

План

1. Введение

2. Исходные данные

3. Исследование на приближение к экспоненциальной зависимости

   1. Построение графика эмпирической зависимости в полулогарифмических координатах

   2. Построение производной

   3. Построение темпа производной

4. Исследование на приближение к степенной зависимости

   1. Построение обратного темпа роста интеграла степенной зависимости

   2. Построение графика BX

   3. Построение графика эмпирической последовательности в логарифмических координатах

5. Заключение

6. Используемая литература

7. Приложение

1. Введение

Анализ эмпирических данных используется в качестве анализа многих экономических показателей для возможности прогнозирования изменения этих показателей. Прогнозированием различной экономической динамики занимаются технический и фундаментальный анализы. Технический анализ по результатам исследования предоставляет конкретное решение по действиям, а на базе фундаментального анализа, можно построить прогноз динамики изменения конкретного показателя в будущем.

В качестве исследуемой последовательности будет взят эмпирический набор экономических данных, имеющий растущую тенденцию изменения во времени.

Данные исследования эмпирических данных будут проводиться с целью выявления некоторых функциональных зависимостей между ними, а также математической модели, к которой наиболее близко приближается эмпирическая зависимость.

В данной курсовой работе будет проведен анализ двух эмпирических последовательностей на соответствие математическим моделям роста, таким как экспоненциальная зависимость и степенная зависимость.

2. Исходные данные

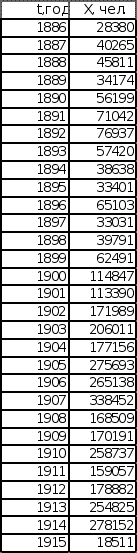
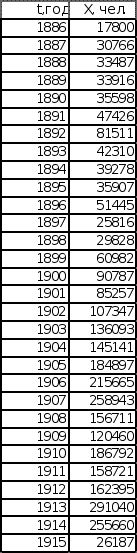
В качестве исходных последовательностей взяты статистические данные из книги «Историческая статистика Соединенных Штатов Америки» – Эмиграция в США из Центральной Европы с 1886 по 1915 год и Эмиграция в США из СССР и стран Балтии с 1886 по 1915 год.

График исходных данных представлен на листе 1 (см. Приложение).

Эмиграция в США Эмиграция в США

из Центральной Европы из СССР и стран Балтии

(Венгрия, Австрия) (Литва, Эстония, Латвия, Финляндия)

3.Исследование на приближение к экспоненциальной зависимости

3.1 Построение графика эмпирической зависимости в полулогарифмических координатах

Уравнение экспоненциальной функции имеет следующий вид:

X=Cekt ,

что является решением дифференциального уравнения:

dX/dt = KX .

Проинтегрировав это уравнение получим линейную зависимость lnX по t:

lnX = kt + lnC .

Эмиграция из Центральной Европы Эмиграция из СССР и стран Балтии

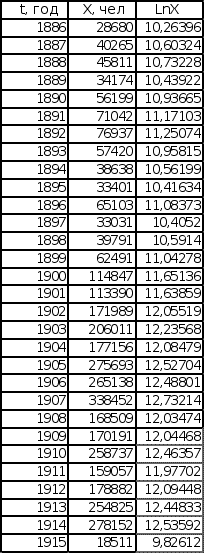
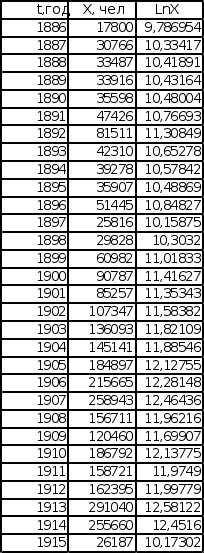
Формула, указанная выше позволяет нам сделать утверждение, что если данные последовательности эмпирических данных приближаются к экспоненте, то график зависимости lnX от времени должен находиться в линейном коридоре.

Иными словами, если последовательность представляет собой экспоненциальную функцию, то ее график в полулогарифмических координатах спрямляется.

По данному графику определяется темп роста, равный

K = 2/1 = (lnX2 – lnX1)/(t2-t1) ,

параметр lnC влияет на расположение прямой на плоскости.

Графики зависимости lnX от t представлены на листе 2 (см. Приложение). Темп роста К, определенный по графикам, равен для графика зависимости Эмиграции в США из Центральной Европы – 0,11, для графика зависимости Эмиграции из СССР и стран Балтии – 0,13.

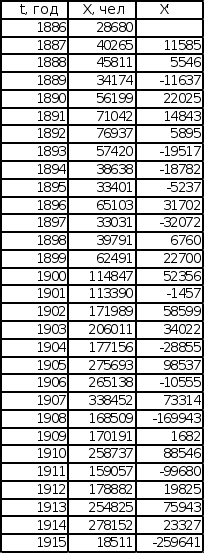
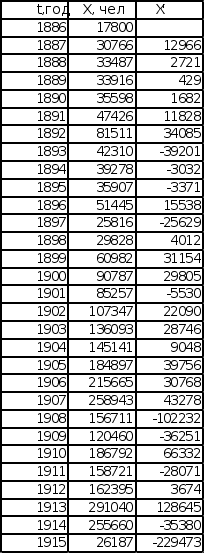
3.2 Построение производной

Производная эмпирической последовательности рассчитывается по формуле:

Xґ(ti) = (Xi – Xi-1)/(ti – ti-1) .

Графики производной изображены на листе 3 (см. Приложение) и представляют собой колебания, имеющие увеличивающуюся амплитуду во времени. Это показывает на то, что скорость роста обеих эмпирических зависимостей во времени увеличивается.

Эмиграция в США из Эмиграция в США из СССР и

Центральной Европы стран Балтии

3.3 Построение темпа производной

График изменения темпа производной строится с использованием формулы:

Xґ(ti)/X(ti) = (Xi – Xi-1)/Xi(ti – ti-1) .

Эмиграция в США из Эмиграция в США из

Центральной Европы СССР и стран Балтии

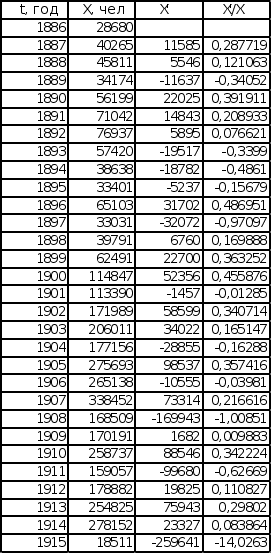
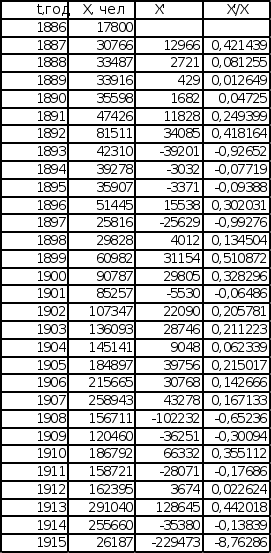
В результате построений получен график, представляющий собой колебания с различной амплитудой относительно прямой, равной темпу роста К, который характеризует скорость роста логарифма эмпирической последовательности.

4. Исследование на приближение к степенной зависимости

4.1 Построение обратного темпа роста интеграла степенной зависимости

Степенная функция имеет вид:

X = X0(t – t0)B ,

который является решением дифференциального уравнения следующего вида:

dX\dt = BX/(t – t0) .

Производная степенной функции равна:

Xґ = BX0(t – t0)B-1 .

Темп роста степенной функции равен:

Xґ/X = B/(t – t0) ,

а обратный темп роста степенной функции имеет следующий вид:

X/Xґ = (t – t0)/B .

Но график обратного темпа имеет очень сильные колебания, что не позволяет с большой точностью отследить тенденцию графика. В следствие этого будет построен график обратного темпа интеграла степенной функции, имеющий более сглаженные колебания и позволяющий достаточно точно определить тегнденцию графика. График обратного темпа интеграла в идеальном случае имеет вид прямой с коэффициентом наклона равным В, которая пересекает ось абсцисс в точке t0.

Интеграл степенной функции вычисляется по формуле :

Y = Xґ(t – t0)B+1/B+1 .

А обратный темп роста интеграла равен:

Yґ/Y = X/Y = (B+1)/(t – t0) .

Коэффициент наклона прямой В может быть найден из графика по формуле:

B = ctg - 1 ,

или, другими словами, разности отношения приращения аргумента (1) к приращению функции (2) и 1.

Обратный темп интеграла степенной зависимости рассчитывается по формуле:

Y/Yґ = (Xt)/X .

Эмиграция в США Эмиграция в США

из Центральной Европы из СССР и стран Балтии

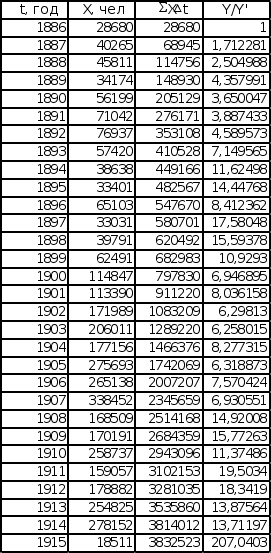
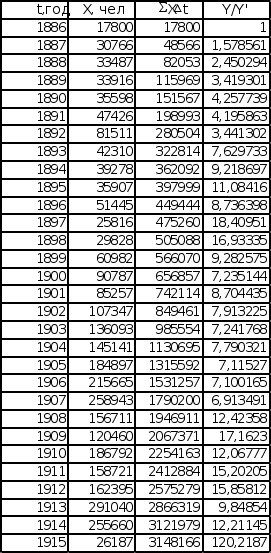
Полученные графики расположены на листе 5 (см. Приложение).

Так как графики зависимостей не имеют ярко выраженной тенденции по приближению к степенной функции, в качестве искомой прямой была взята общая тенденция роста данного графика, полученная с помощью метода наименьших квадратов.

На основе данных графиков получены следующие значения параметров прямой:

• График обратного темпа интеграла зависимости Эмиграция в США из Центральной Европы: t0 = 1877, B = 2.5

• График обратного темпа интеграла зависимости Эмиграция в США из СССР и стран Балтии: t0 = 1875.5, B = 2.9

4.2 Построение графика BX

Для проверки правильности значений коэффициента наклона В и начального времени t0, построен график зависимости BX от времени.

Полученые графики расположены на листе 6 (см. Приложение).

Поскольку, как и в предыдущем случае, невозможно выделить четкую линейную тенденцию графиков эмпирических последовательностей. Поэтому путем проведения прямой через минимумы графика и прямой через максимумы графика, ищется прямая, расположенная на одинаковом расстоянии от обеих прямых.

В результате проведенных построений определились значения t0. В обоих случаях они не совпадают со значениями, полученными в результате предыдущих построений.

• Для последовательности Эмиграция в США из Центральной Европы новое значение t0 = 1890.

• Для последовательности Эмиграция в США из СССР и стран Балтии новое значение t0 = 1883.

Эмиграция в США Эмиграция в США

из Центральной Европы из СССР и стран Балтии

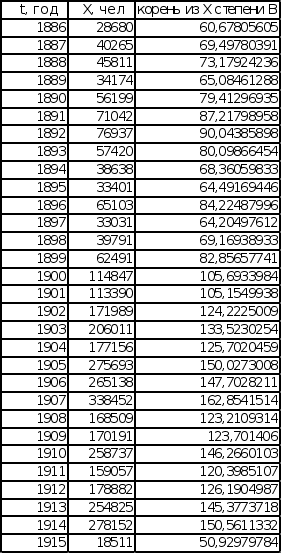
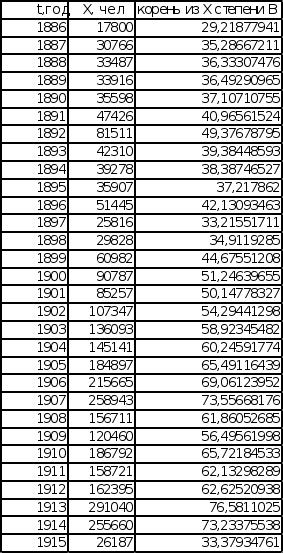
4.3 Построение графика эмпирической последовательности в логарифмических координатах

Как было сказано выше, степенная функция имеет вид:

X = X0(t – t0)B .

Прологарифмировав обе части, получаем линейную зависимость lnX от lnT, где Т = t – t0:

LnX = lnX0 + Bln(t – t0) .

Графики зависимости lnX от lnТ построены с учетом обоих значений t0.

Для значений t0 (t – t0 = T1, t0= 1877 для последовательности Эмиграция в США из Центральной Европы, t0 = 1875,5 для последовательности Эмиграция в США из СССР и стран Балтии), полученных при исследовании графиков обратного темпа роста интеграла эмпирической последовательности, графики имеют вид, представленный на листе 7 (см. Приложение).

Эмиграция в США Эмиграция в США

из Центральной Европы из СССР и стран Балтии

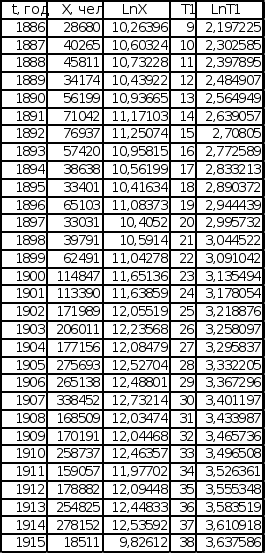
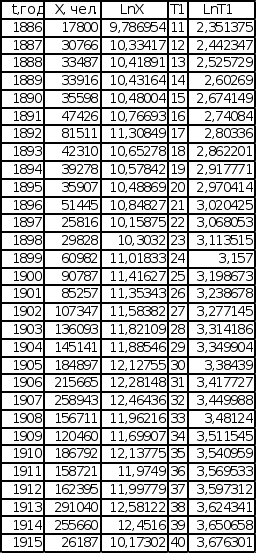
Как и в предыдущем случае, проводится прямая, находящаяся на одинаковом расстоянии от прямой, проведенной через минимумы графика и прямой, проведенной через максимумы графика. Коэффициент наклона данной прямой в этом случае будет равняться

• Для последовательности Эмиграция в США из Центральной Европы В = 2,39;

• Для последовательности Эмиграция в США из СССР и стран Балтии В = 2,73.

Для значений t0 (t – t0 = T2, t0 = 1890 для последовательности Эмиграция в США из Центральной Европы, t0 = 1883 для последовательности Эмиграция в США из СССР и стран Балтии), полученных при исследовании графиков BX , графики имеют вид, представленный на листе 8 (см. Приложение).

Эмиграция в США Эмиграция в США

из Центральной Европы из СССР и стран Балтии

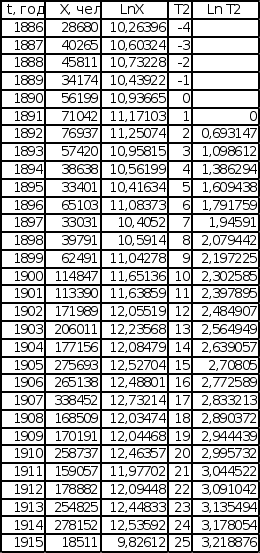
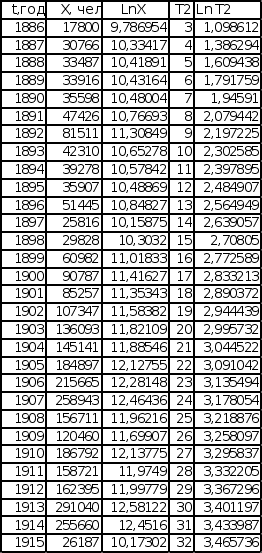
Из аналогично обработанноых графиков эмпирических последовательностей получены новые значения коэффициентов наклона прямых, равные

• Для последовательности Эмиграция в США из Центральной Европы В = 2,44;

• Для последовательности Эмиграция в США из СССР и стран Балтии В = 1,82.

5.Заключение

В результате проведенных исследований были построены графики эмпирических зависимостей и из них получено:

• эмпирическая последовательность Эмиграция в США из Центральной Европы приближается к экспоненциальной зависимости с темпом роста К=0,11

• эмпирическая последовательность Эмиграция в США из СССР и стран Балтии приближается к экспоненциальной зависимости с темпом роста К=0,13

• эмпирическая последовательность Эмиграция в США из Центральной Европы приближается к степенной зависимости с параметрами В и t0. При построении графиков были получены следующие значения параметров:

В=2,5 t0= 1877

В=2,39 t0= 1890

В=2,44

• эмпирическая последовательность Эмиграция в США из СССР и стран Балтии приближается к степенной зависимости с параметрами В и t0. При построении графиков были получены следующие значения параметров:

В= 2,9 t0= 1875,5

В= 2,73 t0= 1883

В= 1,82

6. Используемая литература

1. Statistical History of USA.

7. ПРИЛОЖЕНИЕ