Реферат: Температурный расчет с помощью вычислений информационной математики

Реферат: Температурный расчет с помощью вычислений информационной математики

Постановка задачи.

По длинной квадратного сечения трубе течет горячая жидкость. Труба наполовину погружена в ледяную ванну, так, что температура нижней половины поверхности трубы равна 00 С. Верхняя плоскость трубы имеет постоянную температуру 100 0 С. На участке между ледяной ванной и верхней плоскостью температура наружной поверхности трубы изменяется линейно по высоте от 0 0 С до 100 0 С. Жидкость внутри трубы имеет температуру 200 0 С.

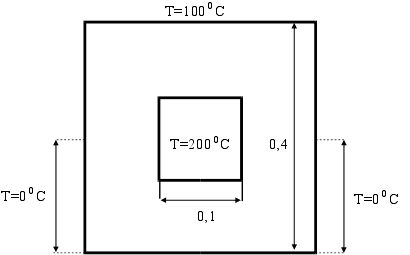
Рис. 3.

Распределение температуры в теле трубы удовлетворяет уравнению

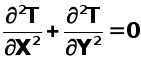
С погрешностью не более 0,5 0 С вычислить распределение температуры в теле трубы.

Математическая формулировка задачи.

Решить диф.уравнение в частных производных:

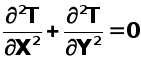
с задаными началиными условиями на границах области дифференцирования.

При решении уравнения приблизительно заменю производные второго порядка конечно-разностными отношениями:

в результате чего диф.уравнение преобразуется в 5-ти диаганальную систему алгеброических уравнений n-го порядка.

Систему алгеброических уравнений буду решать методом Зейделя.

Погрешность решения задачи найду по формуле:

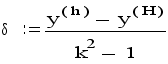
где, и -решения,полученные для одной и той же точки с разными шагами.

Функциональная схема.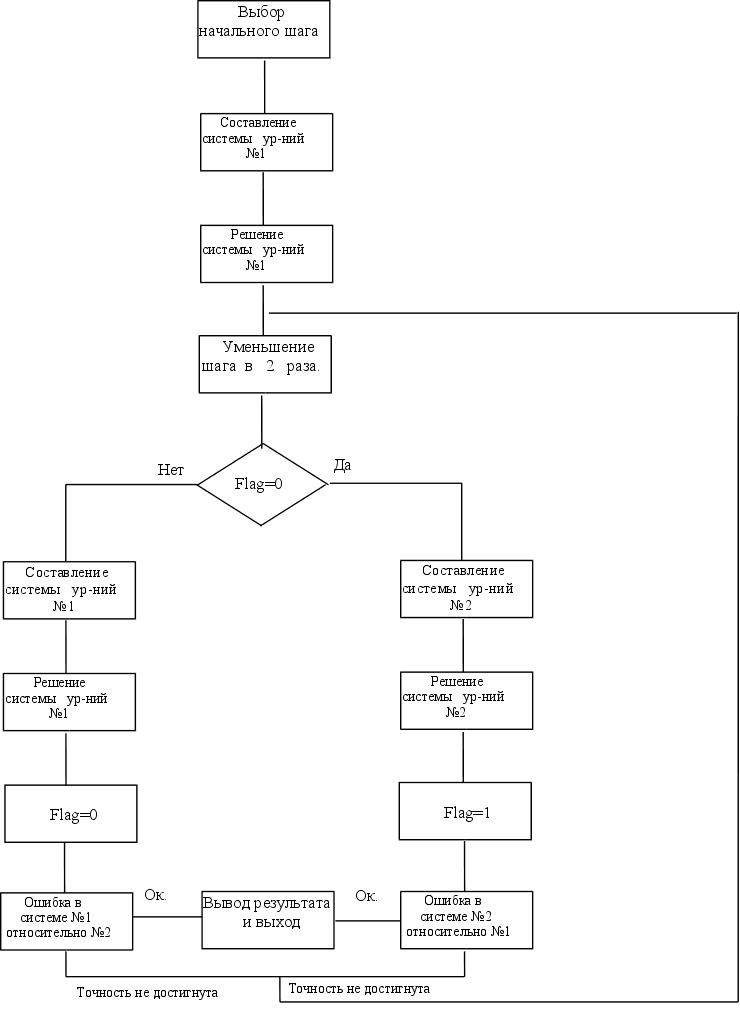

Метод конечных разностей.

Описание метода.

Так назван метод решения краевых задач, основанный на приб­лиженной замене производных, входящих в дифференциальные урав­нения и краевые условия, нонечно-разностными отношениями. Эта замена позволяет свести краевую задачу к задаче решения системы алгебраических уравнений.

Конечные разности и производные.Пусть некоторая функция y(x) задана на отрезке [a,b]. Будем считать, что она непрерывна и многократно дифференциру­ема на этом отрезке. Разделим отрезок на равные части длиною h и обозначим точки деления x0,x1,...,xi,...,xn.Значе­ния функции в этих точках обозначим соответственно y0,y1,...,yi,...,yn.Первой центральной разностью в i-й точке (i=1,2,...,n-1) называют разность:

С помощью этой разности можно приближенно вычислить значение первой производной у` в i-й точке.

Разложим функцию y(x) в степенной ряд. приняв за центр разложения точку xi и ограничившись четырьмя членами:

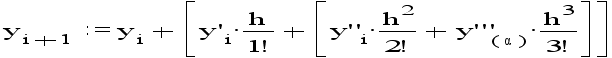
где

Аналогично найдем значение ф-ции и в точке,отстоящей от центра разложения на шаг (-h):

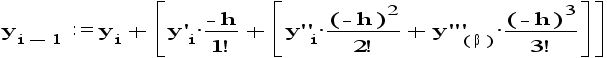
где .

Подставляя получим:

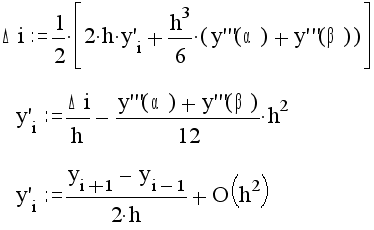
Таким образом,производная y` приближонно заменяется конечно-разностным отношением с ошибкой порядка h*h:

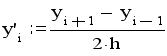
Второй центральной разностью ф-ции y(x) в i-й точке называют величину:

С помощью этой разности можно приближонно вычислить значение второй производной y`` в i-й точке.Используем теперь 5 членов разложения в ряд Тейлора:

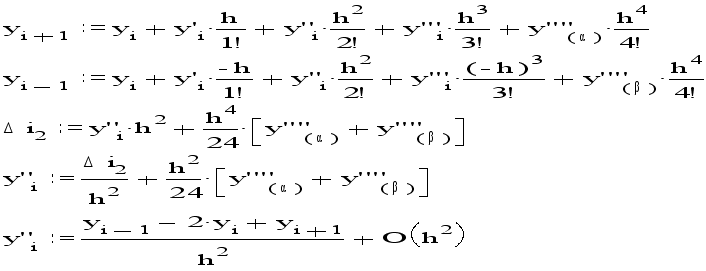
Таким образом,вторая производная y`` с ошибкой порядка h*h может быть приближонно заменена конечно-разностным отношением:

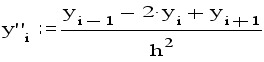
При определении разностей в i -и точке использовались значения функции в точках, расположенных симметрично относительно xi . Поэтому эти разности назы­ваются центральными.

Существуют также левые и правые разности, использующие точки, расположенные соответственно левее и правее точки xi. С помощью этих разностей можно также приближенно вычислять значения производных, но погрешность при этом будет больше -порядка h.

Разностные системы уравнений составляются в следующем порядке.

1. Исходное дифференциальное уравнение преобразуют к та­кой форме, чтобы затем получить из него наиболее простую разностную систему уравнений. При этом учитывают, что коэффициен­ты при производных войдут в разностную схему одновременно в несколько ее членов и затем будут распространены на всю систе­му уравнений. Поэтому желательно иметь единичные коэффициенты при производных в исходном уравнении.

2. На интервале интегрирования исходного уравнения уста­навливают равномерную сетку с шагом h и записывают разностную схему, приближенно заменяя производные соответствующими цент­ральными конечно-разностными отношениями.

3.Применяя разностную схему для узлов сетки записывают разностные уравнения. При этом можно получить уравнения содержащие так называемые внеконтурные неизвестные, то есть неизвестные в точках, лежащих за пределами установленной сет­ки.

4.В разностной форме записывают краевые условия и состав­ляют полную систему разностных уравнений.

Оценка погрешности решения краевой задачи

Решение разностной системы уравнений дает приближенное решение краевой задачи. Поэтому возникает вопрос о точности этого приближенного решения.

Для линейных краевых задач доказана теорема о том, что по­рядок точности решения краевой задачи не ниже порядка точности аппроксимации производных конечно-разностными отношениями. Оценку погрешности производят при­емом Рунге. Краевую задачу решают дважды: с шагом сетки h и с шагом сетки H=kh, погрешность решения с малым шагом h оценивают по формуле:

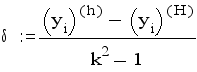
где y(h) и y(H) - решения, полученные для одной и той же точ­ки -xi отрезка интегрирования с разными шагами. Относительную погрешность E оценивают по формуле:

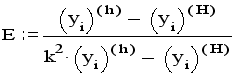
Если при составлении разностной системы уравнений исполь­зуются левые или правые разности, то погрешность решения будет выше, порядка 0(h), и для ее оценки в формулах следует заменить k*k на k .

Применение метода конечных разностей для решения уравнений в частных проиэводных

Для применения разностного метода в области изменения не­зависимых переменных вводят некоторую сетку. Все производные, входящие в уравнение и краевые условия, заменяют разностями значений функции в узлах сетки и получают таким образом алгебраическуго систему уравнений. Решая эту систему, находят приб­лиженное решение задачи в узлах сетки.

Блок схема.

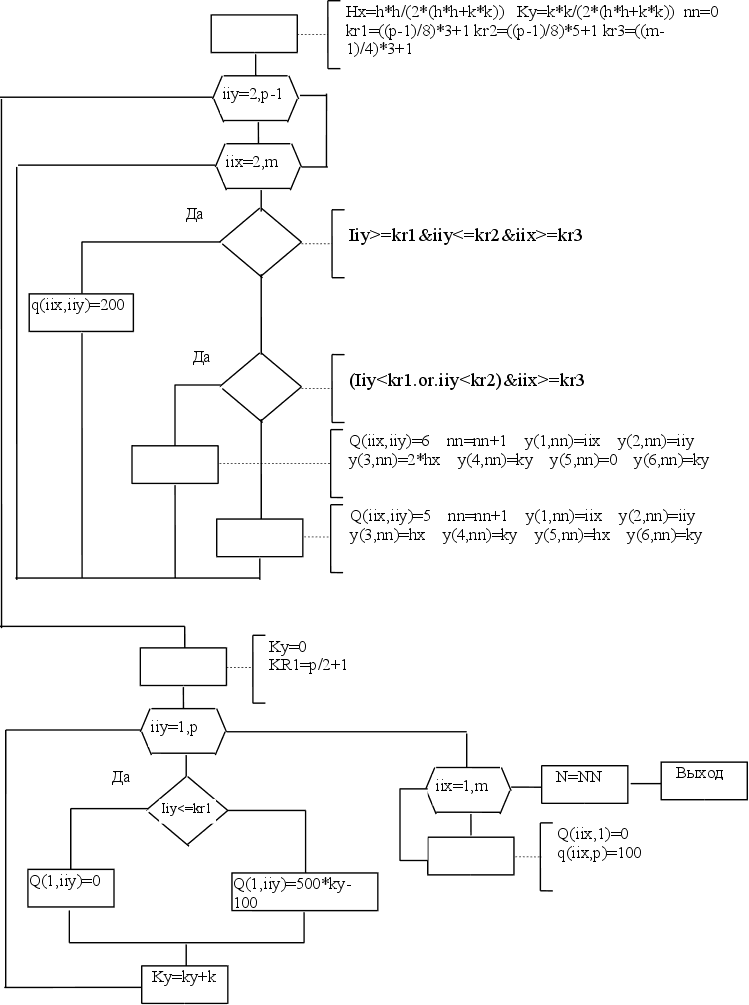
Подпрограмма МКР.

c------------------------------------------------------------------

c ПОДПРОГРАММА СОСТАВЛЕНИЯ СИСТЕМЫ УРАВНЕНИЙ

c МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ

c

c real H-шаг по оси X

c real K-шаг по оси Y

c real N-количество уравнений(примерное число,желательно N=M*P)

c real y(6,N)-выходной массив уравнений,содержащий следующие поля:

c y(1,N)-номер точки по оси X

c y(2,N)-номер точки по оси Y

c y(3,N)-коэфициен уравнения для Q(y(1,N)-1,y(2,N))

c y(3,N)=h^2/(2*(h^2+k^2))

c y(4,N)-коэфициен уравнения для Q(y(1,N),y(2,N)-1)

c y(4,N)=k^2/(2*(h^2+k^2))

c y(5,N)-коэфициен уравнения для Q(y(1,N)+1,y(2,N))

c y(5,N)=h^2/(2*(h^2+k^2))

c y(6,N)-коэфициен уравнения для Q(y(1,N),y(2,N)+1)

c y(6,N)=k^2/(2*(h^2+k^2))

c integer M-число узлов по оси X

c integer P-число узлов по оси Y

c real Q(M,P)-массив значений Y

c integer N-выходное количество получившихся уравнений

c------------------------------------------------------------------

subroutine mkr(H,K,N,y,M,P,q)

integer M,P,IIX,IIY,NN,N,KR1,KR2,KR3

real y(6,N),H,K,q(M,P),HX,KY

c-----------------------------------------------------------------

c подсчитываю коэфициенты

c h^2/(2*(h^2+k^2))

c и

c k^2/(2*(h^2+k^2))

c-----------------------------------------------------------------

HX=H**2/(2*(H**2+K**2))

KY=K**2/(2*(H**2+K**2))

c-----------------------------------------------------------------

c составление уравнений

c и

c присваивание начальных значений

c

c nn-счетчик уровнений

c iix-номер текущего узла по оси X

c iiy-номер текущего узла по оси Y

c-----------------------------------------------------------------

NN=0

KR1=((P-1)/8)*3+1

KR2=((P-1)/8)*5+1

KR3=((M-1)/4)*3+1

do IIY=2,P-1

do IIX=2,M

if (NN.eq.N)then

print *,'ПЕРЕПОЛНЕНИЕ МАССИВА Y'

stop

endif

c-----------------------------------------------------------------

c проверка границы трубы с жидкостью

c-----------------------------------------------------------------

if ((IIY.ge.KR1).and.(IIY.le.KR2).and.(IIX.ge.KR3)) then

q(IIX,IIY)=200.

c-----------------------------------------------------------------

c проверка симметрии

c-----------------------------------------------------------------

elseif (((IIY.lt.KR1).or.(IIY.gt.KR2)).and.(IIX.eq.M)) then

q(IIX,IIY)=6

NN=NN+1

y(1,NN)=IIX

y(2,NN)=IIY

y(3,NN)=2*HX

y(4,NN)=KY

y(5,NN)=0

y(6,NN)=KY

c-----------------------------------------------------------------

c составление уравнений во внутренних точках фигуры

c-----------------------------------------------------------------

else

q(IIX,IIY)=5

NN=NN+1

y(1,NN)=IIX

y(2,NN)=IIY

y(3,NN)=HX

y(4,NN)=KY

y(5,NN)=HX

y(6,NN)=KY

endif

enddo

enddo

c-----------------------------------------------------------------

c присваивание начальных значений на границе фигуры

c------------------------------------------------------------------

KY=0

KR1=P/2+1

do IIY=1,P

if (IIY.le.KR1)then

q(1,IIY)=0

else

q(1,IIY)=500*KY-100

endif

KY=KY+K

enddo

do IIX=1,M

q(IIX,1)=0

q(IIX,P)=100

enddo

N=NN

end

ТЕСТ

Для тестирования составлю разностную систему с шагом вдоли оси X и Y=0.05

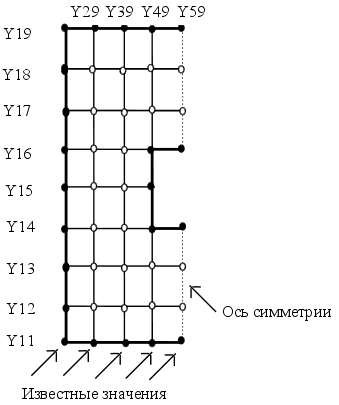
Неизвестные значения в узлах матрицы находящихся внутри фигуры высчитываются по формуле:

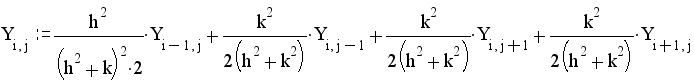
Неизвестные значения в узлах матрицы находящихся на оси симметрии высчитываются по формуле:

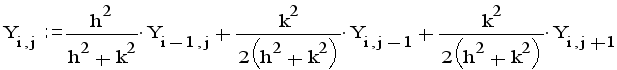
МЕТОД ЗЕЙДЕЛЯ.

Метод Зейделя относится к числу итерационных методов, в которых принципиально отсутствует фактор накопления погрешностей. Поэтому он широко применяется для решения больших систем уравне­ний. Будем рассматривать корни решаемой системы как компоненты некоторого вектора у . Основная идея всех итерационных методов заключается в том, что берется приближенное значение вектора у и по формулам, составленным на основании решаемых уравнений, вычис­ляется новое приближенное значение вектора у . Назовем эти при­ближенные значения y(k) и y(k+1) соответственно. Поскольку ис­ходное приближение выбиралось произвольно, то у(k+1)в свою очередь может послужить исходным для получения по тем же формулам нового приближения y(k+2) . Очевидно, этот процесс можно продолжать сколь угодно долго. Говорят, что процесс итераций сходится, если получаемая при этом последовательность векторов у(k) (к=0,1,2,...} имеет своим пределом вектор y,являющийся точным решением системы:

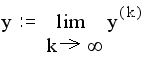
На практике невозможно достигнуть этого предела, но можно прибли­зиться н нему с любой наперед заданной точностью. Так и поступают задаются некоторой погрешностью, вектором начального приближе­ния и получают последовательные приближения до тех пор, пока дей­ствительная погрешность корней не станет меньше заданной.

Различные методы отличаются друг от друга способом вычисления очередного приближения, но во всех методах существуют две главные проблемы:

обеспечение сходимости процесса итераций;

оценка достигнутой погрешности.

Пусть дана линейная система

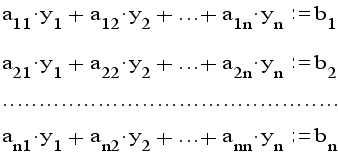
Предполагая, что диагональные коэффициенты

aii<>0 (i=1,2,..,n)

разрешим первое уравнение относительно y1 , второе - относите­льно y2 и т.д.

Тогда получим эквивалентную систему

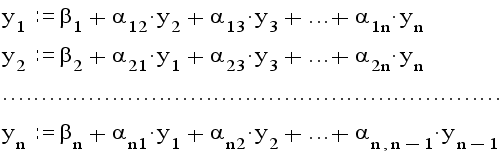
где

при i<>j

и

при i=j (i,j=1,2,...,n)

Такую систему будем в дальнейшем называть приведенной.

Метод Зейделя заключается в следующем. Выбрав вектор началь­ного приближения

y(ср)=(y1,y2,...,yn)

подставим его компоненты в правую часть первого уравнения систе­мы и вычислим первую компоненту y`1 нового вектора y`(ср) . В правую часть второго уравнения подставим компоненты (y`1,y2,y3,...,yn) и вычислим вторую компоненту y`2'нового вектора. В третье уравнение подставим (y`1,y`2,y3,...,yn) и т.д. Очевидно,подстановкой в каждое уравнение мы, дойдя до последнего уравнения, обновим все компоненты исходного вектора и получим первое приближение к ре­шению

y`(ср)=(y`1,y`2,y`3,...,y`n)

Далее , взяв в качестве исходного вектор у`(ср) , выполним вторую итерацию и получим y``(ср). Этот процесс будем продолжать до до­стижения заданной степени точности.

Оценка погрешности приближений процесса Зейделя

Для оценки погрешности прежде всего вычисляют показатель скорости сходимости

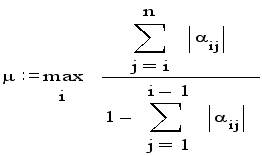
То есть для каждой строки матрицы коэффициентов системы вычисляется сумма модулей коэффициентов, лежащих правее главной диагонали :

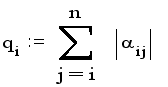
и сумма модулей коэффициентов, лежащих левее главной диагонали:

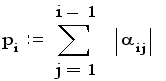
Для каждой i-й строки (i =1,2,...,n ) вычисляется отноше­ние

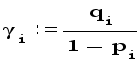
и в качестве берется максимальное из этих отношений. Чем меньше окажется , тем большей будет скорость сходимости.

Для процесса Зейделя справедлива следующая оценка погрешнос­ти К-го приближения:

(i,j=1,2,...,n)

то есть модуль отклонения любого i -го корня системы в К-м приближении от точного значения того же корня не больше, чем умноженное на множитель максимальное из при­ращений корней, полученных в результате перехода от (K-1) -го приближения к К-му.

Если задаться абсолютной погрешностью и потребовать выполнения условия

(j=1,2,...,n)

то выполнится и условие

(i=1,2,3,...,n),

то есть заданная степень точности на К-й итерации будет достигнута. На практике это означает, что после каждой итерации необходимо вы­делить тот корень, изменение которого по сравнению с предыдущим значением оказалось наибольшим по модулю. Модуль приращения этого корня необходимо умножить на и сравнить результат с выбран­ной абсолютной погрешностью.

Достаточные условия сходимости процесса Зейделя

Если модули коэффициентов системы удовлетворяют хотя бы одному из условий

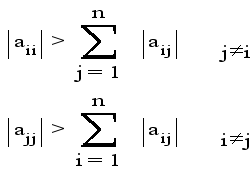(i,j=1,2,3,...,n)

то процесс Зейделя для соответствующей приведенной системы сходит­ся к её единственному решению при любом выборе начального вектсра y(ср) Такие системы называют системами с диагональным преоблада­нием.

Метод Зейдедя имеет свойство, позволяющее обеспечить сходимость процесса для любых систем уравнений с неособенной матрицей коэфициентов.

Если обе части систем с неособенной матрицей коэфициентов А=[aij] умножить слева на транспонировнную матриц A*[aij] , то будет получена новая, равносильная исходной система, которая называется нормальной. Процесс Зейделя для приведенной системы, полученной из нормальной, всегда сходится независимо от выбора нача льного приближения.

Блок схема.

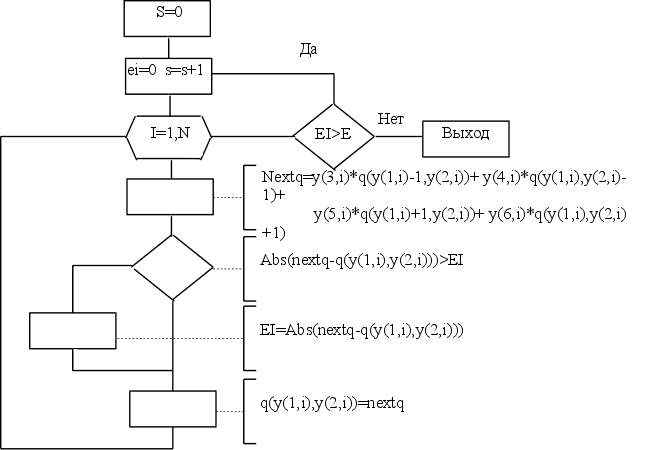
Подпрограмма метода Зейделя.

c-----------------------------------------------------------------

cПОДПРОГРАММА РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ МЕТОДОМ ЗЕЙДЕЛЯ

c

с integer N-входное количество уравнений

c real y(6,N)-входной массив уравнений,содержащий следующие поля:

c y(1,N)-номер точки по оси X

c y(2,N)-номер точки по оси Y

c y(3,N)-коэфициен уравнения для Q(y(1,N)-1,y(2,N))

c y(3,N)=h^2/(2*(h^2+k^2))

c y(4,N)-коэфициен уравнения для Q(y(1,N),y(2,N)-1)

c y(4,N)=k^2/(2*(h^2+k^2))

c y(5,N)-коэфициен уравнения для Q(y(1,N)+1,y(2,N))

c y(5,N)=h^2/(2*(h^2+k^2))

c y(6,N)-коэфициен уравнения для Q(y(1,N),y(2,N)+1)

c y(6,N)=k^2/(2*(h^2+k^2))

c integer M-число узлов по оси X

c integer P-число узлов по оси Y

c real Q(M,P)-входной массив начальных значений Y

c real Q(M,P)-выходной массив вычисленых значений Y

c real E-погрешность вычислений

c------------------------------------------------------------------

subroutine zeidel(N,y,M,P,q,E)

integer N,M,P,I,S

real y(6,N),q(M,P),E,EI,NEXTQ

c------------------------------------------------------------------

c вычисление коэфициента сходимости процесса

c mj=y(5,1)+y(6,1)

c и выражения

c km=mj/(1-mj)

C НО Т.К. MJ=0.5 ТО KM=1 И СЛЕДОВАТЕЛЬНО ЕГО МОЖНО ОПУСТИТЬ

c-----------------------------------------------------------------

c KM=(y(5,1)+y(6,1))/(1-y(5,1)+y(6,1))

c------------------------------------------------------------------

c итерации

c S-счетчик итераций

c------------------------------------------------------------------

S=0

1 EI=0.

S=S+1

do I=1,N

NEXTQ=y(3,i)*Q(y(1,i)-1,y(2,i))+

+ y(4,i)*Q(y(1,i),y(2,i)-1)+

+ y(5,i)*Q(y(1,i)+1,y(2,i))+

+ y(6,i)*Q(y(1,i),y(2,i)+1)

c------------------------------------------------------------------

c вычисление погрешности на данной итерации

c------------------------------------------------------------------

if (abs(NEXTQ-q(y(1,i),y(2,i))).gt.EI)

+ EI=abs(NEXTQ-q(y(1,i),y(2,i)))

c print *,'x=',y(1,i),' y=',y(2,i)

q(y(1,i),y(2,i))=NEXTQ

enddo

c print '(16h Итерация номер ,i5,13h погрешность=,E15.7)',S,EI

if (EI.gt.E)goto 1

c do i=P,1,-1

c print '(21e10.3)',(q(j,i),j=1,M)

c enddo

end

ТЕСТ

В качестве теста выполним одну итерацию для системы , полученной в предыдущем пункте.

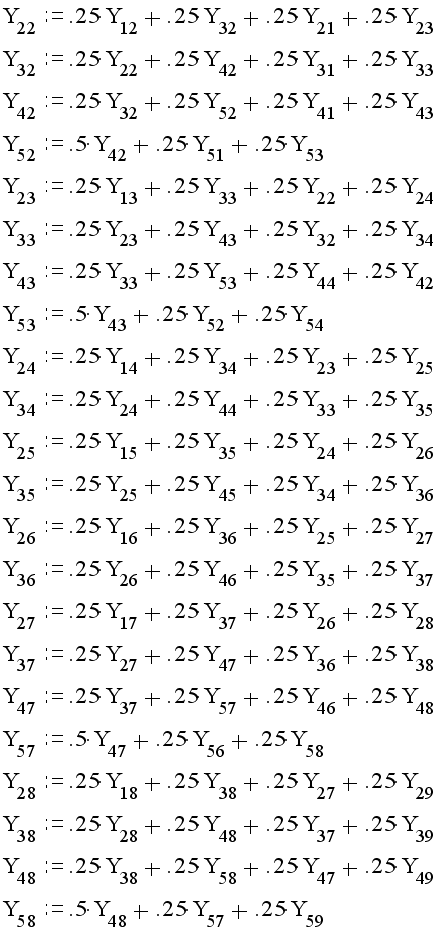
при начальных условиях:

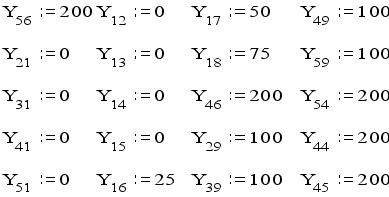
все остальные Yij:=0.

Получается:

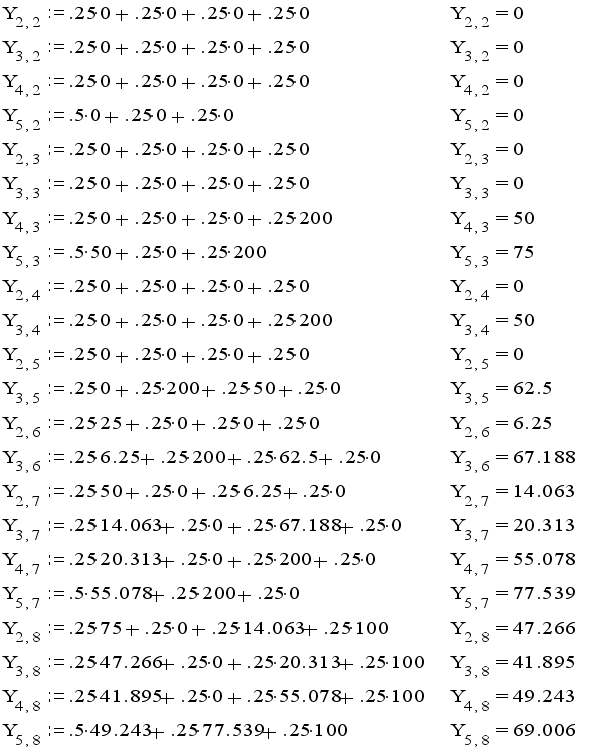
Результат:

Полный текст программы.

c------------------------------------------------------------------

c ПОДПРОГРАММА СОСТАВЛЕНИЯ СИСТЕМЫ УРАВНЕНИЙ

c МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ

c

c real H-шаг по оси X

c real K-шаг по оси Y

c real N-количество уравнений(примерное число,желательно N=M*P)

c real y(6,N)-выходной массив уравнений,содержащий следующие поля:

c y(1,N)-номер точки по оси X

c y(2,N)-номер точки по оси Y

c y(3,N)-коэфициен уравнения для Q(y(1,N)-1,y(2,N))

c y(3,N)=h^2/(2*(h^2+k^2))

c y(4,N)-коэфициен уравнения для Q(y(1,N),y(2,N)-1)

c y(4,N)=k^2/(2*(h^2+k^2))

c y(5,N)-коэфициен уравнения для Q(y(1,N)+1,y(2,N))

c y(5,N)=h^2/(2*(h^2+k^2))

c y(6,N)-коэфициен уравнения для Q(y(1,N),y(2,N)+1)

c y(6,N)=k^2/(2*(h^2+k^2))

c integer M-число узлов по оси X

c integer P-число узлов по оси Y

c real Q(M,P)-массив значений Y

c integer N-выходное количество получившихся уравнений

c------------------------------------------------------------------

subroutine mkr(H,K,N,y,M,P,q)

integer M,P,IIX,IIY,NN,N,KR1,KR2,KR3

real y(6,N),H,K,q(M,P),HX,KY

c-----------------------------------------------------------------

c подсчитываю коэфициенты

c h^2/(2*(h^2+k^2))

c и

c k^2/(2*(h^2+k^2))

c-----------------------------------------------------------------

HX=H**2/(2*(H**2+K**2))

KY=K**2/(2*(H**2+K**2))

c-----------------------------------------------------------------

c составление уравнений

c и

c присваивание начальных значений

c

c nn-счетчик уровнений

c iix-номер текущего узла по оси X

c iiy-номер текущего узла по оси Y

c-----------------------------------------------------------------

NN=0

KR1=((P-1)/8)*3+1

KR2=((P-1)/8)*5+1

KR3=((M-1)/4)*3+1

do IIY=2,P-1

do IIX=2,M

if (NN.eq.N)then

print *,'ПЕРЕПОЛНЕНИЕ МАССИВА Y'

stop

endif

c-----------------------------------------------------------------

c проверка границы трубы с жидкостью

c-----------------------------------------------------------------

if ((IIY.ge.KR1).and.(IIY.le.KR2).and.(IIX.ge.KR3)) then

q(IIX,IIY)=200.

c-----------------------------------------------------------------

c проверка симметрии

c-----------------------------------------------------------------

elseif (((IIY.lt.KR1).or.(IIY.gt.KR2)).and.(IIX.eq.M)) then

q(IIX,IIY)=6

NN=NN+1

y(1,NN)=IIX

y(2,NN)=IIY

y(3,NN)=2*HX

y(4,NN)=KY

y(5,NN)=0

y(6,NN)=KY

c-----------------------------------------------------------------

c составление уравнений во внутренних точках фигуры

c-----------------------------------------------------------------

else

q(IIX,IIY)=5

NN=NN+1

y(1,NN)=IIX

y(2,NN)=IIY

y(3,NN)=HX

y(4,NN)=KY

y(5,NN)=HX

y(6,NN)=KY

endif

enddo

enddo

c-----------------------------------------------------------------

c присваивание начальных значений на границе фигуры

c------------------------------------------------------------------

KY=0

KR1=P/2+1

do IIY=1,P

if (IIY.le.KR1)then

q(1,IIY)=0

else

q(1,IIY)=500*KY-100

endif

KY=KY+K

enddo

do IIX=1,M

q(IIX,1)=0

q(IIX,P)=100

enddo

N=NN

end

c-----------------------------------------------------------------

c ПОДПРОГРАММА РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ МЕТОДОМ ЗЕЙДЕЛЯ

c

с integer N-входное количество уравнений

c real y(6,N)-входной массив уравнений,содержащий следующие поля:

c y(1,N)-номер точки по оси X

c y(2,N)-номер точки по оси Y

c y(3,N)-коэфициен уравнения для Q(y(1,N)-1,y(2,N))

c y(3,N)=h^2/(2*(h^2+k^2))

c y(4,N)-коэфициен уравнения для Q(y(1,N),y(2,N)-1)

c y(4,N)=k^2/(2*(h^2+k^2))

c y(5,N)-коэфициен уравнения для Q(y(1,N)+1,y(2,N))

c y(5,N)=h^2/(2*(h^2+k^2))

c y(6,N)-коэфициен уравнения для Q(y(1,N),y(2,N)+1)

c y(6,N)=k^2/(2*(h^2+k^2))

c integer M-число узлов по оси X

c integer P-число узлов по оси Y

c real Q(M,P)-входной массив начальных значений Y

c real Q(M,P)-выходной массив вычисленых значений Y

c real E-погрешность вычислений

c------------------------------------------------------------------

subroutine zeidel(N,y,M,P,q,E)

integer N,M,P,I,S

real y(6,N),q(M,P),E,EI,NEXTQ

c------------------------------------------------------------------

c вычисление коэфициента сходимости процесса

c mj=y(5,1)+y(6,1)

c и выражения

c km=mj/(1-mj)

C НО Т.К. MJ=0.5 ТО KM=1 И СЛЕДОВАТЕЛЬНО ЕГО МОЖНО ОПУСТИТЬ

c-----------------------------------------------------------------

c KM=(y(5,1)+y(6,1))/(1-y(5,1)+y(6,1))

c------------------------------------------------------------------

c итерации

c S-счетчик итераций

c------------------------------------------------------------------

S=0

1 EI=0.

S=S+1

do I=1,N

NEXTQ=y(3,i)*Q(y(1,i)-1,y(2,i))+

+ y(4,i)*Q(y(1,i),y(2,i)-1)+

+ y(5,i)*Q(y(1,i)+1,y(2,i))+

+ y(6,i)*Q(y(1,i),y(2,i)+1)

c------------------------------------------------------------------

c вычисление погрешности на данной итерации

c------------------------------------------------------------------

if (abs(NEXTQ-q(y(1,i),y(2,i))).gt.EI)

+ EI=abs(NEXTQ-q(y(1,i),y(2,i)))

c print *,'x=',y(1,i),' y=',y(2,i)

q(y(1,i),y(2,i))=NEXTQ

enddo

c print '(16h Итерация номер ,i5,13h погрешность=,E15.7)',S,EI

if (EI.gt.E)goto 1

c do i=P,1,-1

c print '(21e10.3)',(q(j,i),j=1,M)

c enddo

end

c------------------------------------------------------------------

c ПОДПРОГРАММА АЛФАВИТНО-ЦИФРОВОГО,МОЗАИЧНОГО

c ВЫВОДА РЕЗУЛЬТАТА

c integer M-число узлов по оси X

c integer P-число узлов по оси Y

c real Q(M,P)-входной массив значений Y

c

c

c------------------------------------------------------------------

subroutine outdata(M,P,q)

character a(11)/'.','+','*','','','-','-','-','','-','-'/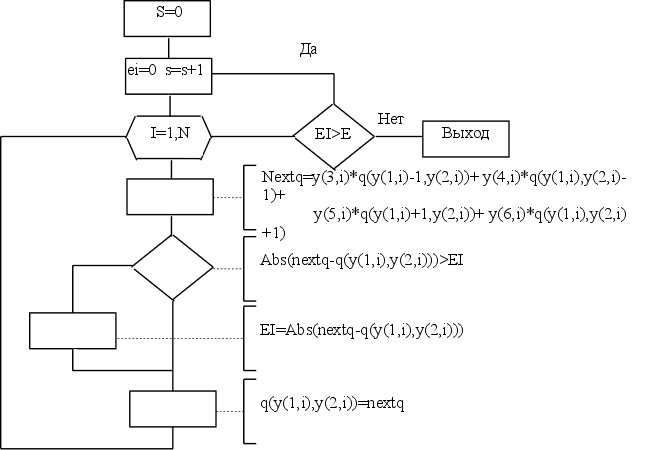

integer M,P,I,J

real q(M,P)

do J=P,1,-1

print '(400A2)',(a(int(q(I,J)/21)+1),I=1,M),

+ (a(int(q(I,J)/21)+1),I=M-1,1,-1)

enddo

do I=1,10

print *,'''',a(I),'''','---> от ',20*(I-1),', до ',

+ 20*I,'(включительно)'

enddo

end

c------------------------------------------------------------------

c ПОДПРОГРАММА ВЫЧИСЛЕНИЯ ОШИБКИ

c real q-массив значений Y с шагом =2*h

c real qq-массив значений Y с шагом =h

c real E-значение погрешности

c

c------------------------------------------------------------------

subroutine mistake(M,P,q,qq,E)

integer M,P,iq,jq,iqq,jqq

real qq(M,P),q(int(M/2)+1,int(P/2)+1),max,E,other

max=0

iq=0

do iqq=1,P,2

iq=iq+1

jq=0

do jqq=1,M,2

jq=jq+1

other=abs(q(jq,iq)-qq(jqq,iqq))

if (other.gt.max)max=other

enddo

enddo

print *,M,' ',P,' ',max/3

if (max/3.lt.E) then

call outdata(M,P,qq)

Stop

endif

end

c------------------------------------------------------------------

c ОСНОВНАЯ ПРОГРАММА

c

c

c------------------------------------------------------------------

integer N/90000/,M,P,flag/0/

real y(6,90000),q(300,300),H/.05/,K/.05/,E/.5/,qq(300,300)

real EZ/.01/

c print *,'Введите шаг вдоль оси X '

c read (*,*)H

c print *,'Введите шаг вдоль оси Y '

c read (*,*)K

c print *,'Введите точность вычислений '

c read (*,*)E

M=.2/H+1

P=.4/K+1

call mkr(H,K,N,y,M,P,q)

call zeidel(N,y,M,P,q,EZ)

111 H=H/2

K=K/2

M=.2/H+1

P=.4/K+1

N=90000

if (flag.eq.0)then

flag=1

call mkr(H,K,N,y,M,P,qq)

call zeidel(N,y,M,P,qq,EZ)

call mistake(M,P,q,qq,E)

else

flag=0

call mkr(H,K,N,y,M,P,q)

call zeidel(N,y,M,P,q,EZ)

call mistake(M,P,qq,q,E)

endif

goto 111

end

Литература.

1. И.С.Березин,Н.П.Жидков ’Методы вычислений’,том 1,М.,1966,632 стр.

2.’ Численные методы решения задач на ЭВМ ’ , Учебное пособие , Г.Н.Рубальченко , К. , 1989 , 148 стр.

3.’Справочник языка ФОРТРАН’ , М.,1996 ,106 стр.

Температурный расчет с помощью вычислений информационной математики.