
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология и педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по информатике программированию
Краткое содержание произведений
Реферат: Способ определения живучести связи (вероятности связности)
Реферат: Способ определения живучести связи (вероятности связности)
СПОСОБ ОПРЕДЕЛЕНИЯ ЖИВУЧЕСТИ.
Определению живучести связи (вероятности связности) между двумя конкретными узлами сети i и j посвящен целый ряд работ [1-5]. Однако расчет точного ее назначения сопряжен с большими вычислительными трудностями. Представляет интерес найти простой способ определения вероятности связности сети, который позволял бы оперативно и вручную проводить на стадии проектирования оценку различных вариантов их построения.
Рассмотрим
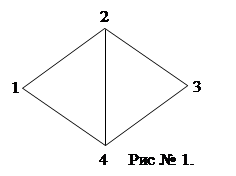
сеть той же мостиковой структуры, что и в [1] (рис.1). Для простоты будем
полагать вероятности исправного функционирования всех ребер сети одинаковыми и
равными р , а неисправного функционирования - равными q=1-p.
Для оценки живучести воспользуемся
методом прямого перебора состояний элементов сети связи [5]. На основании
биноминального закона вероятность пребывания сети связи в состоянии, когда i
любых ребер сети отказали,![]() , где
, где ![]() - биноминальный
коэффициент; N – число ребер сети.
- биноминальный
коэффициент; N – число ребер сети.
Например, для сети, изображенной на рис. 1, живучесть связи р13 зависит от следующей
совокупности
независимых событий: исправного состояния сети в целом – вероятность этого
события равна р3; повреждения любого одного ребра сети –
вероятность ![]() одновременного повреждения
любых двух ребер сети, за исключением двух случаев, когда оба ребра подходят к
узлу 1 или к узлу 3 – вероятность
одновременного повреждения
любых двух ребер сети, за исключением двух случаев, когда оба ребра подходят к
узлу 1 или к узлу 3 – вероятность![]() одновременного
повреждения трех ребер сети, подходящих к узлу 2 или 4 – вероятность 2р2q3.
одновременного
повреждения трех ребер сети, подходящих к узлу 2 или 4 – вероятность 2р2q3.
Суммируя все вероятности независимых событий, получаем искомое выражение :
![]()
что полностью совпадает полученными результатами в [1].
Аналагично для всех остальных пар узлов сети рис. № 1.
![]()
![]()
Из анализа видно, что
![]()
Связанной сетью являются сеть, в которой любой из узлов соединен с остальными узлами сети. Вероятность связанности сети рис. № 1
![]()
так как эта сеть допускает все одиночные повреждения ребер и восемь двойных повреждений ребер. Вероятность связности сети меньше или равна живучести связи между любой парой узлов сети, в данном случае рс<р13.
С точки зрения характеристики сети интерес представляют вероятность рс, минимальная рмин и максимальная рмакс живучести связи между любой парой узлов сети и соотношения между ними. Для сети рис №1: рс < рмин = р13 < р12 = р14 = р23 = р34 < р24 =рмакс.
Аналогично можно найти выражения для вероятности связности полносвязных сетей. Для сети с тремя вершинами (n=3)
![]() (1)
(1)
для n=4;
![]() (2)
(2)
для n=5;
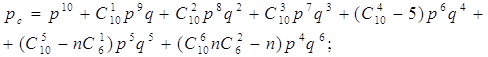 (3)
(3)
для n=6;
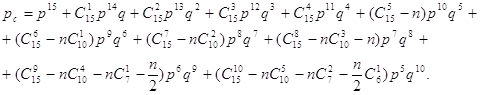 (4)
(4)
Для рс при n=7….10 расчетные формулы не приводятся из-за громоздкости.
Вероятность связности для кольцевых сетей связи, т.е. сетей, у которых степень для каждой вершины равна 2 (степенью вершины d называются число граней графа сети, инцидентных данной вершине [6]),
![]()
На рис 2 определена зависимость рс от р для кольцевых сетей при различных n. Из ее анализа видно, что вероятность связности кольцевых сетей падает с увеличением числа узлов сети при одних и тех же значениях р.
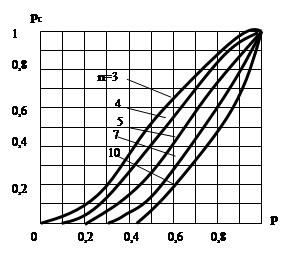
Рис № 2.
На практике довольно редко встречаются полносвязные сети. Обычно бывают сети с небольшими степенями вершин. Имеется большое семейство графов (так называемых равнопрочных) , в которых степень вершины d, число вершин n и общее число граней m связаны следующим соотношением: d=2m/n (при n>2).
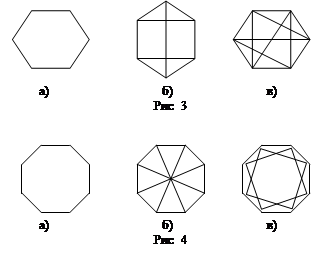
Например для шестиугольника (n=6) без резервирования связей можно построить четыре различных графа с d=2, 3, 4, 5. Вероятности связности этих графов определяется следующими выражениями:
При d=2 (рис. 3,а)
![]() (5)
(5)
при d=3 (рис. 3,б)
![]() (6)
(6)
при d=4 (рис. 3,в)
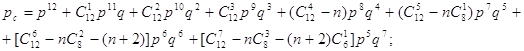 (7)
(7)
При n=8 можно построить шесть различных графов с d=2…..7; вероятность связности этих графов определится следующими выражениями:
d=2 (рис. 4,а)
![]() (8)
(8)
d=3 (рис. 4,б)
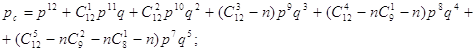 (9)
(9)
d=4 (рис. 4,в)
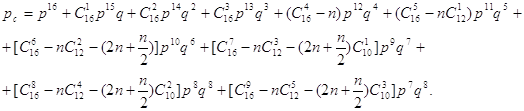 (10)
(10)
 |
 |
Расчетные формулы для рс при d=5 и 6 из-за громоздкости не приводятся.
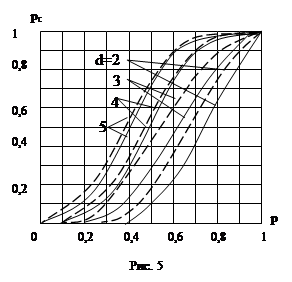
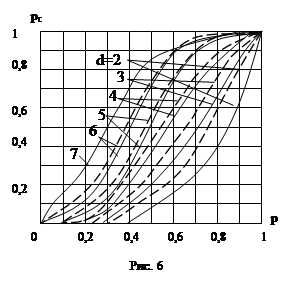
На рис 5 и 6 представлены зависимости вероятности связности сети с n=6, 8 соответственно при различных d (сплошные линии), построенные по формулам (5) – (10). Из рисунков видно, что увеличение вероятности связности сети с увеличением d при неизменном p объясняется тем , что с увеличением d возрастает разветвленность сети связи.
К сожалению, ловольно трудно получить аналитическое выражение для вероятности связности сети рассматренного семейство графов при различных d и n, за исключением полносвязных сетей с d = n – 1 [см.выражение (1) – (4)]. По этому целесобразно определять верхнюю груницу вероятности связности графов. Если граф связный, то в нем не может быть изолированных вершин. В этом случае каждой вершине должна быть инцидента по крайней мере одна ветвь.
Пусть Ai – событие, когда не существует неповрежденных ветвей, инцидентных вершине i, p(Ai) – вероятность этого события; 1 – p(Ai) – вероятность дополнительного события, когда существует по крайней мере одна целая ветвь, инцидентная вершине i, Поэтому вероятность того, что у всех вершин есть по крайне мере одна целая ветвь, т.е. есть связана, ограничена неравенством:
![]() (11)
(11)
На рис. 5,6 представлены зависимости (11) для n=6, и d=2…..7 (штриховые линии). Сравнение кривых показывает, что верхнюю границу вероятности связности сети, особенно при больших d.
Таким образом, полученная простая верхняя оценка вероятности связности равнопрочных сетей связи дает шорошее приближение к точному значению вероятности связности сети при больших значениях d.