Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология и педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по информатике программированию
Краткое содержание произведений
Реферат: Синтез комбинацонных схем и конечных автоматов, сети Петри
Реферат: Синтез комбинацонных схем и конечных автоматов, сети Петри
Государственный комитет Российской Федерации по высшему образованию
Кубанский государственный технологический университет
Кафедра ???
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе по предмету
математические основы теории систем
тема курсовой работы:
« Синтез комбинационных схем и конечных
автоматов. Сети Петри ».
Выполнил : студент гр. ??–??–??
????
номер зачётной книжки ??–??–???
Руководитель : ????
????
???
1999
Государственный комитет Российской Федерации по высшему образованию
Кубанский государственный технологический университет
ЗАДАНИЕ
![]() На
курсовую работу
На
курсовую работу
![]() Студенту
гр.
Студенту
гр.
По дисциплине
Тема курсовой работы
Исходные данные
1 Выполнить расчёты:
1.1
![]()
1.2
![]()
![]() 1.3
1.3
![]() 1.4
1.4
2 Выполнить графические работы:
![]() 2.1
2.1
![]() 2.2
2.2
3 Выполнить научные и учебно-исследовательские работы:
3.1
![]()
3.2
![]()
3.3
![]()
3.4
![]()
4 Оформить расчётно-пояснительную записку
5 Основная литература
Задание выдано
![]()
Срок сдачи работы
![]()
Задание принял
![]()
Руководитель
![]()
Работа защищена
![]()
С оценкой
![]()
ЧЛЕНЫ КОМИССИИ :
РЕФЕРАТ
МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ, КОМБИНАЦИОННАЯ СХЕМА, МИНИМИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ, АВТОМАТ МИЛИ, СЕТЬ ПЕТРИ.
Первая часть курсовой работы посвящена минимизации булевых функций двумя различными способами, а также построению комбинационных схем в базисах, состоящих всего из одной функции.
Вторая часть содержит основные понятия и определения из теории конечных автоматов, а также пример их использования для конкретного автомата. Сюда входит минимизация конечных автоматов по числу состояний, минимизация булевых функций, описывающих комбинационную часть с последующей реализацией полученного автомата на логических элементах из определённого базиса и элементах памяти – триггерах и задержках.
В третьей части рассмотрены вопросы анализа функционирования и программного моделирования сетей Петри. Разными способами исследованы поведенческие свойства заданной сети Петри. Составлена простейшая программа, моделирующая все возникающие в сети ситуации.
Курсовая работа содержит 38 страниц, 11 рисунков, 8 таблиц,
4 источника, 1 приложение .
СОДЕРЖАНИЕ
Введение ………………………………………………………………6
1 Синтез комбинационных схем
1.1 Постановка задачи ……………………………………………… 7
1.2 Теоретические сведения …………………………………………7
1.3 Расчёты и полученные результаты ……………………………..9
1.4 Выводы по разделу………………………………………………13
2 Синтез конечных автоматов
2.1 Постановка задачи ……………………………………………… 14
2.2 Теоретические сведения …………………………………………14
2.3 Расчёты и полученные результаты …………………………… 16
2.4 Выводы по разделу……………………………………………… 20
3 Сети Петри
3.1 Постановка задачи ……………………………………………… 21
3.2 Теоретические сведения ……………………………………… 21
3.3 Расчёты и полученные результаты …………………………… 26
3.4 Выводы по разделу……………………………………………… 31
Заключение …………………………………………………………. 32
Литература ………………………………………………………… 33
Приложение А ……………………………………………………… 34
ВВЕДЕНИЕ
Работа посвящена синтезу дискретных устройств с “памятью” (конечных автоматов) и “без памяти” (комбинационных схем), а также анализу реально протекающих процессов с помощью сетей Петри.
В первой части рассмотрена минимизация булевых функций, заданных в виде СДНФ, с помощью двух различных способов : карт Карно и метода склеивания Квайна – МакКласки. Полученные в виде минимизированных ДНФ функции были приведены к базисам, состоящим всего из одной функции : И – НЕ и ИЛИ – НЕ , а затем реализованы в виде комбинационных схем на соответствующих логических элементах.
Во второй части заданный по условию в функциональном виде конечный автомат был минимизирован по числу состояний. Для полученного автомата был построен граф состояний. Затем, перейдя к двоичному представлению входных, выходных сигналов и сигналов состояния, в автомате были выделены элементы памяти и комбинационная часть, которая затем была минимизирована по числу переменнных. Автомат был реализован в базисе И – ИЛИ – НЕ с использованием D - триггера и задержки.
В третьей части была проанализирована заданная сеть Петри с помощью двух способов: матричного и основанного на построении дерева покрываемости, а также написана программа для её моделирования.
1 Синтез комбинационных схем
1.1 Постановка задачи
Для двух булевых функций, построенных по варианту задания в виде
![]() (1.1.1)
(1.1.1)
![]() ,
(1.1.2)
,
(1.1.2)
где gi, zi – десятичные числа из диапазона от 0 до 15 в двоичном виде,
сделать следующее:
а) представить F1 и F2 в виде СДНФ.
б) минимизировать (по количеству переменных в ДНФ) F1 с
помощью карт Карно, F2 – методом Квайна-МакКласки.
в) реализовать в виде комбинационной схемы на логических элементах F1 – в базисе И – НЕ, F2 – в базисе ИЛИ – НЕ, предварительно приведя F1 и F2 к соответствующим базисам.
gi и zi вычислять по выражениям:
![]() (1.1.3)
(1.1.3)
![]() (1.1.4)
(1.1.4)
при
g0 = A, z0 = B .
Параметр ![]() изменять от 1 до тех пор, пока не будет получено 9
различных значений gi и zi.
изменять от 1 до тех пор, пока не будет получено 9
различных значений gi и zi.
1.2 Теоретические сведения.
Булевой алгеброй называется множество S объектов A, B, C…,
в котором определены две бинарные
операции (логическое сложение – дизъюнкция(+) и логическое умножение –
конъюнкция(∙)) и одна унарная операция(логическое отрицание(![]() )). Оно обладает следующими
свойствами:
)). Оно обладает следующими
свойствами:
а) Для ![]() A,
B, C
A,
B, C ![]() S
S
1)
![]()
![]() ,
, ![]() (замкнутость);
(замкнутость);
2)
![]()
![]() (коммутативные
законы);
(коммутативные
законы);
3)
![]()
![]() (ассоциативные
законы);
(ассоциативные
законы);
4)
![]() (дистрибутивные законы);
(дистрибутивные законы);
5)
![]() (свойства
идемпотентности);
(свойства
идемпотентности);
6)
![]() в
том и только том случае, если
в
том и только том случае, если
![]() (свойство совместимости);
(свойство совместимости);
7)
S содержит
элементы 1 и 0 такие, что для всякого элемента ![]()
![]() ;
;
8) для каждого элемента A класс S содержит элемент Ã (дополнение элемента A, часто обозначаемое символами Ā или 1- A ) такой, что
![]() ,
, ![]() .
.
В каждой булевой алгебре
![]() (законы поглощения),
(законы поглощения),
![]() (законы склеивания),
(законы склеивания),
![]()
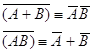 (двойственность, законы де Моргана).
(двойственность, законы де Моргана).
Если даны n булевых переменных X1, X2,…, Xn, каждая из которых может быть равна любому элементу булевой алгебры, то булевой функцией называется выражение
![]() (1.2.1)
(1.2.1)
В
каждой булевой алгебре существует ровно ![]() различных
булевых функций n переменных.
различных
булевых функций n переменных.
Система булевых функций называется полной (базисом), если любая функция может быть представлена в виде суперпозиции функций выбраной системы.
Под критерим минимизации (упрощения) булевых функций будем понимать достижение минимума букв в записи функции.
Введём понятие многомерного куба.
Любую булеву функцию n переменных, заданную в ДНФ или СДНФ, можно отобразиь на n-мерном кубе, построенном в ортогональном базисе n булевых переменных. Каждое слагаемое в ДНФ или СДНФ представляется гиперплоскостью соответствующей размерности: если оно представляет собой конъюнкцию n переменных – точка, n-1 переменных – прямая, n-2 переменных – плоскость и т.д. Элементы n-мерного куба, имеющие s измерений, назовём s-кубами.
Комплекс K(y) кубов функции y=ƒ(x1,x2,…,xn) есть объединение Ks(y) множеств всех её кубов. Отсутствующие в конъюнкциях переменные будем обозначать через x.
1.3 Расчёты и полученные результаты.
По варианту задания находим gi и zi:
|
i |
gi |
zi |
|
0 |
5 |
0 |
|
1 |
1 |
6 |
|
2 |
8 |
2 |
|
3 |
5 |
9 |
|
4 |
13 |
6 |
|
5 |
11 |
14 |
|
6 |
4 |
12 |
|
7 |
3 |
5 |
|
8 |
13 |
4 |
|
9 |
13 |
14 |
|
10 |
8 |
14 |
|
11 |
9 |
9 |
|
12 |
5 |
10 |
|
13 |
7 |
6 |
Неповторяющиеся значения gi: 5, 1, 8, 13, 11, 4, 3, 9, 7. Неповторяющиеся значения zi: 0, 6, 2, 9, 14, 12, 5, 4, 10. Таким образом, для F1 получаем выражение
![]() , (1.3.1)
, (1.3.1)
для F2:
![]() . (1.3.2)
. (1.3.2)
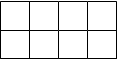
Для минимизации первой функции применяем метод карт Карно.
Карта Карно – прямоугольник с 2n клетками, каждой из которых соответствует своя конъюнкция из n переменных и их отрицаний (дополнений).
Проставляя единицы в соответствующих клетках, выбираем затем минимальную из всех возможных комбинацию покрытий. Применим карту Карно к заданной функции:
x3x4
 00 01
11 10
00 01
11 10
00 1 1
01 1 1 1
x1x2
11 1
10 1 1 1
Рисунок 1.2.1 – карта Карно
На основании выбранной комбинации покрытий выписываем минимизированное выражение для функции F1:
![]() .
(1.3.3)
.
(1.3.3)
Для второй функции применяем метод Квайна-МакКласки.
На первом шаге алгоритма выписываем комплекс K0-кубов заданной функции, упорядоченных по возрастанию количества единиц:
0 0 0 0 0 1 1 1 1
0 0 1 1 1 0 0 1 1
K0 = 0 1 0 0 1 0 1 0 1 (1.3.4)
0 0 0 1 0 1 0 0 0 .
Второй этап основан на операции склеивания. Каждый из кубов проверяется на “склеиваемость” со всеми остальными. Склеивающиеся кубы должны различаться не более чем в одном разряде. Склеенный разряд в дальнейшем обозначается как x. Куб, участвовавший в операции склеивания, соответствующим образом помечается. Поскольку таких кубов мало, будем отмечать не участвовавшие в операции склеивания кубы. В результате получаем комплекс K1-кубов, также упорядоченный по возрастанию количества единиц в разрядах:
![]()
![]() 0 0 0 x 0 0 x
x 1 1
0 0 0 x 0 0 x
x 1 1
0 x x 0 1 1 1 1 x 1
K1 = x 0 1 1 0 x 0 1 1 x (1.3.5)
0 0 0 0 x 0 0 0 0 0 .
Повторяем вышеописанную операцию для комплекса K1-кубов, после чего удаляем из полученного комплекса K2-кубов повторяющиеся:
![]()
![]()
![]()
![]()
![]()
![]() 0 0 x x x
x 0 x x
0 0 x x x
x 0 x x
x x x x 1 1 x x 1
K2 = x x 1 1 x x = x 1 x (1.3.6)
0 0 0 0 0 0 0 0 0
Те кубы, которые не участвовали в операциях склеивания, называются импликантами – это кандидаты на то, чтобы попасть в итоговую ДНФ. Для них составляем таблицу покрытий K0-кубов. Импликанта считается покрывающей K0-куб, если они совпадают при x, принимающем произвольное значение.
|
K0 z |
0 0 0 0 |
0 0 1 0 |
0 1 0 0 |
0 1 0 1 |
0 1 1 0 |
1 0 0 1 |
1 0 1 0 |
1 1 0 0 |
1 1 1 0 |
Импликанты |
|
1001 |
+ |
|
||||||||
|
010x |
+ | + |
|
|||||||
|
0xx0 |
+ | + | + | + |
|
|||||
|
xx10 |
+ | + | + | + |
|
|||||
|
x1x0 |
+ | + | + | + |
|
Таблица 1.3.1 – Покрытия K0-кубов
Существенной импликантой, или экстремалью, называется такая импликанта, которая в единственном числе покрывает хотя бы один из K0-кубов.
Из таблицы следует, что все импликанты являются экстремалями. Следовательно, они все войдут в запись функции в виде сокращённой ДНФ:
![]() .
(1.3.7)
.
(1.3.7)
Комбинационная схема – это дискретное устройство, каждый из выходных сигналов которого в момент времени tm определяется так:
yj(tm) = ƒ ( x1(tm), x2(tm),…,xn(tm)) , (1.3.8)
где ![]() . Видно, что выходной сигнал в m-й момент времени определяется только комбинацией
входных сигналов в данный момент и не зависит от их предыдущих значений.
Поэтому комбинационную схему можно реализовать на логических элементах,
выполняющих операции из определённого базиса булевых функций.
. Видно, что выходной сигнал в m-й момент времени определяется только комбинацией
входных сигналов в данный момент и не зависит от их предыдущих значений.
Поэтому комбинационную схему можно реализовать на логических элементах,
выполняющих операции из определённого базиса булевых функций.
Приведём F1 к базису И – НЕ, а F2 – к базису ИЛИ – НЕ:
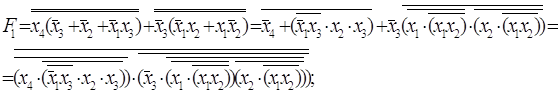 (1.3.9)
(1.3.9)
![]()
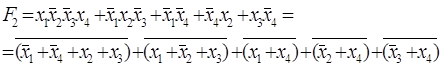 . (1.3.10)
. (1.3.10)
Получив выражения для функций, приведённых к соответствующим базисам, можно нарисовать комбинационные схемы, реализующие эти функции, на элементах одного вида: для первой функции это будут И – НЕ-элементы, для второй – ИЛИ – НЕ :
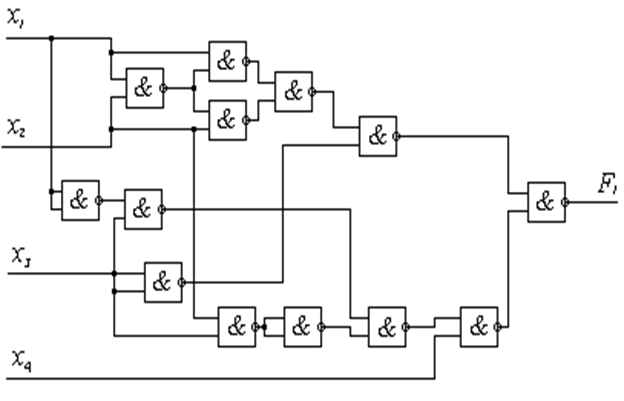
Рисунок 1.3.1 – Схема на И – НЕ-элементах
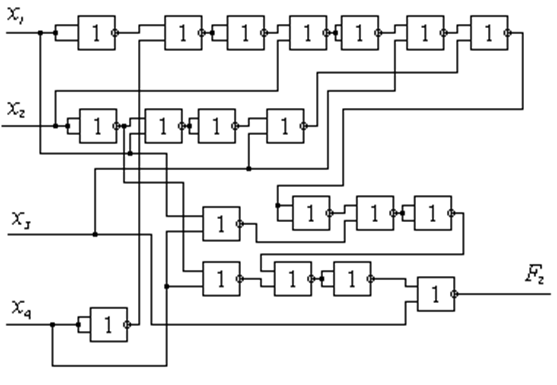
Рисунок 1.3.2 – Схема на ИЛИ – НЕ-элементах
1.4 Выводы по разделу
В первой части были рассмотрены примеры минимизации (упрощения) булевых функций двумя разными способами. Была практически показана возможность приведения функций двух аргументов к базису, состоящему всего из одной функции. Были построены комбинационные схемы, иллюстрирующие полученные результаты. Выгода рассмотренных преобразований функций становится очевидной при их практической реализации на стандартизованных электронных микросхемах.
2 Синтез конечных автоматов
2.1 Постановка задачи
Конечный автомат задан своими уравнениями переходов и выходов:
s(j+1) = [2∙s(j) + x(j) + B] mod 8 ,
y(j) = [ s(j) + x(j) + A] mod 2 ,
![]() .
.
Требуется:
а) построить таблицы переходов, выходов и общую таблицу переходов автомата;
б) минимизировать автомат по числу состояний с использованием таблиц, полученных ранее;
в) построить граф минимизированного автомата и выписать для него матрицу переходов;
г) переходя ко двоичному представлению входа X, выхода Y и состояния S, составить таблицу входов и выходов комбинационной схемы автомата и выполнить минимизацию булевых функций, соответствующих выходам и состояниям автомата;
д) разработать логическую схему автомата в базисе И – НЕ, реализуя элементы памяти на триггерах и задержках.
2.2 Теоретические сведения
Конечным автоматом называется такое дискретное устройство, выходные сигналы которого в определённые моменты времени зависят не только от последнего пришедшего входного сигнала, но и от некоторого количества предыдущих его значений.
Различают синхронные и асинхронные автоматы. У асинхронных смена выходных сигналов y(tj) может происходить только в моменты изменения входных x(tj) , у синхронных – в моменты времени, определяемые дополнительным синхронизирующим сигналом c(t) .
Определим множества, которым могут принадлежать входные и выходные сигналы (условимся обозначать tj как j):
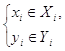 – множетва
входных и выходных сигналов.
– множетва
входных и выходных сигналов.
Тогда выражения
![]() (2.2.1)
(2.2.1)
определяют входной и выходной алфавиты автомата.
Пусть ![]() . Тогда
если y(j) = λ(x(j)), то этот автомат
является, очевидно, комбинационной схемой.
. Тогда
если y(j) = λ(x(j)), то этот автомат
является, очевидно, комбинационной схемой.
Введём дополнительную переменную для того, чтобы охарактеризовать состояние автомата в каждый момент времени j:
![]() (2.2.2)
(2.2.2)
В том случае, если X, Y и S – конечные множества, то и сам автомат называют конечным.
В виде уравнений любой конечный автомат можно записать разными способами. Одна из возможных форм записи:
![]() (2.2.3)
(2.2.3)
Записанный таким образом автомат называется автоматом Мили. Ясно, что это – более информативная форма записи по сравнению с автоматом Мура:
![]()
![]() (2.2.4)
(2.2.4)
Способы задания автоматов.
Во - первых, автомат может быть задан непосредственно уравнениями вида (2.2.3) или (2.2.4).
Во - вторых, уравнения (2.2.3) и (2.2.4) могут быть представлены в табличной форме. Табличный аналог первого уравнения в (2.2.3) называется таблицей переходов, второго – таблицей выходов.
В - третьих, таблицы переходов и выходов можно объединить в одну. Содержимое каждой клетки представляет собой дробь: над косой чертой вписывается соответствующее значение из таблицы переходов, под косой чертой – значение из таблицы выходов. Полученная таким образом таблица называется общей таблицей переходов и выходов конечного автомата.
Граф автомата – это сигнальный граф, вершины которого обозначают состояния автомата, на дугах отражены условия перехода из состояния в состояние и значения выходных сигналов в виде дроби: над косой чертой – x(j), под ней – y(j).
Конечный
автомат можно также описать с помощью матрицы переходов. Это аналог графа в
табличной форме. Она представляет собой квадратную матрицу размерности число
состояний ![]() число состояний, в которой
отражены условия перехода из состояния в состояние аналогично изображённым на
графе.
число состояний, в которой
отражены условия перехода из состояния в состояние аналогично изображённым на
графе.
Общее определение конечного автомата:
M = (X, Y, S, δ, λ), (2.2.5)
где X – входной алфавит, Y – выходной алфавит, S – множество состояний, δ – функция переходов, λ – функция выходов.
Пусть имеется два автомата: M и M’.
Если
для любого ![]() существует по крайней мере
одно
существует по крайней мере
одно ![]() , эквивалентное ему, то
говорят, что M’ покрывает M:
M’ ≥ M.
, эквивалентное ему, то
говорят, что M’ покрывает M:
M’ ≥ M.
Если одновременно M’ ≥ M и M ≥ M’, то M ~ M’ . Получаем эквивалентные автоматы. В этом случае невозможно различить M и M’ по их реакции на входные сигналы.
Существуют два основных положения определения понятия эквивалентности состояний:
а) состояния si и sj явно различны, если соответствующие им строки в таблице выходов разные;
б) состояния si и sj явно эквивалентны, если соответствующие им строки в общей таблице переходов автомата одинаковы или становятся таковыми при замене si на sj или наоборот.
Минимизация (упрощение) автоматов основано на понятии эквивалентных автоматов. Под минимизацией автомата будем понимать сокращение числа его состояний.
2.3 Расчёты и полученные результаты.
Построение таблиц переходов, выходов и общей таблицы переходов и выходов на основе заданных уравнений автомата Мили очевидно:
|
s(j) |
0 |
1 |
2 |
3 |
|
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
2 |
1 |
0 |
1 |
0 |
|
3 |
0 |
1 |
0 |
1 |
|
4 |
1 |
0 |
1 |
0 |
|
5 |
0 |
1 |
0 |
1 |
|
6 |
1 |
0 |
1 |
0 |
|
7 |
0 |
1 |
0 |
1 |
Таблица 2.3.1 – Таблица выходов автомата
|
s(j) |
0 |
1 |
2 |
3 |
|
0 |
0 |
1 |
2 |
3 |
|
1 |
2 |
3 |
4 |
5 |
|
2 |
4 |
5 |
6 |
7 |
|
3 |
6 |
7 |
0 |
1 |
|
4 |
0 |
1 |
2 |
3 |
|
5 |
2 |
3 |
4 |
5 |
|
6 |
4 |
5 |
6 |
7 |
|
7 |
6 |
7 |
0 |
1 |
Таблица 2.3.2 – Таблица переходов автомата
|
s(j) |
0 |
1 |
2 |
3 |
|
0 |
0/1 |
1/0 |
2/1 |
3/0 |
|
1 |
2/0 |
3/1 |
4/0 |
5/1 |
|
2 |
4/1 |
5/0 |
6/1 |
7/0 |
|
3 |
6/0 |
7/1 |
0/0 |
1/1 |
|
4 |
0/1 |
1/0 |
2/1 |
3/0 |
|
5 |
2/0 |
3/1 |
4/0 |
5/1 |
|
6 |
4/1 |
5/0 |
6/1 |
7/0 |
|
7 |
6/0 |
7/1 |
0/0 |
1/1 |
Таблица 2.3.3 – Общая таблица переходов и выходов автомата
Перейдём непосредственно к минимизации полученного автомата по числу состояний. Для этого воспользуемся алгоритмом, известным в литературе как метод Гриса - Хопкрофта. Его достоинство в том, что он даёт гарантированно минимальную форму автомата. Однако в общем случае он является довольно трудоёмким и применяется, как правило, для автоматов с небольшим количеством состояний. Он основан на свойстве транзитивности эквивалентности
(si ~ sj)
∩ (sj ~ sk) ![]() (si
~ sk)
(2.3.1)
(si
~ sk)
(2.3.1)
Пара эквивалентных состояний переходит при всех возможных значениях входа в пары также эквивалентных состояний.
Алгоритм состоит из следующих шагов.
Сначала разбиваем все состояния автомата на множества по признаку совпадения выходных сигналов. В нашем случае получаем 2 множества: S1 = {0, 2, 4, 6} и S2 = {1, 3, 5, 7}.
Чтобы назвать каждый из полученных классов новым состоянием, нужно убедиться в том, что в каждый класс входят только эквивалентные между собой состояния. Для этого составляем таблицу пар эквивалентных состояний. При этом не забываем о том, что эквивалентными могут быть состояния, принадлежащие только одному классу. В таблицу заносим все те пары, в которые переходят при соответствующих входах исходные, вероятно эквивалентные, пары:
|
пары |
0 |
1 |
2 |
3 |
|
0;2 |
0;4 |
1;5 |
2;6 |
3;7 |
|
0;4 |
0;0 |
1;1 |
2;2 |
3;3 |
|
0;6 |
0;4 |
1;5 |
2;6 |
3;7 |
|
2;4 |
4;0 |
5;1 |
6;2 |
3;7 |
|
2;6 |
4;4 |
5;5 |
6;6 |
7;7 |
|
4;6 |
0;4 |
1;5 |
2;6 |
3;7 |
|
1;3 |
2;6 |
3;7 |
4;0 |
5;1 |
|
1;5 |
2;2 |
3;3 |
4;4 |
5;5 |
|
1;7 |
2;6 |
3;7 |
4;0 |
5;1 |
|
3;5 |
6;2 |
7;3 |
0;4 |
1;5 |
|
3;7 |
6;6 |
7;7 |
0;0 |
1;1 |
|
5;7 |
2;6 |
3;7 |
4;0 |
5;1 |
Таблица 2.3.4 – Таблица пар эквивалентных состояний
Ищем в полученной таблице неэквивалентные пары – пары из разных множеств. В таблице таких нет, значит, окончательно получаем автомат с двумя новыми состояниями – обозначим их 0 и 1.
Следующим шагом оформляем общую таблицу переходов для минимизированной формы автомата:
|
s(j) |
0 |
1 |
2 |
3 |
|
0 |
0/1 |
1/0 |
0/1 |
1/0 |
|
1 |
0/0 |
1/1 |
0/0 |
1/1 |
Таблица 2.3.5 – Новая общая таблица переходов.
На основании полученной общей таблицы переходов и выходов можно нарисовать граф минимизированного автомата с двумя состояниями:
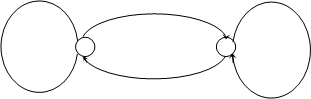 0/1U 2/1 1/0 U 3/0 1/1U 3/1
0/1U 2/1 1/0 U 3/0 1/1U 3/1
0 1
0/0 U 2/0
Рисунок 2.3.1 – Граф минимизированного автомата
Для практической реализации полученного автомата надо двоично закодировать все сигналы. Для кодировки y и s достаточно одного двоичного разряда, x требует двух – x1 и x2:
|
x |
x1 |
x2 |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
2 |
1 |
0 |
|
3 |
1 |
1 |
Таблица 2.3.6 – Двоичная кодировка x
Составляем таблицу истинности для комбинационной части схемы на основе таблицы (2.3.5). Получаем две функции трёх аргументов:
|
x1(j) |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
x2(j) |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
s(j) |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
y(j) |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
s(j+1) |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
Таблица 2.3.7 – Таблица истинности комбинационной части
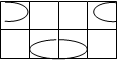
Каждую из функций y(j) и s(j+1) минимизируем с помощью карт Карно:
y(j) s(j+1)
x1(j)x2(j) x1(j)x2(j)
 00 01 11
10 00 01 11 10
00 01 11
10 00 01 11 10
0 1 1 0 1 1
s(j) s(j)
1 1 1 1 1 1
Рисунок 2.3.2 – Карты Карно для комбинационной части
На основании выбранных покрытий записываем минимизированные выражения для функций переходов и выходов:
![]() (2.3.2)
(2.3.2)
![]() (2.3.3)
(2.3.3)
Реализуем полученные функции в виде комбинационной схемы, добавляя к ней элементы памяти – D - триггер и задержку. Комбинационную часть реализуем в базисе И – ИЛИ – НЕ.
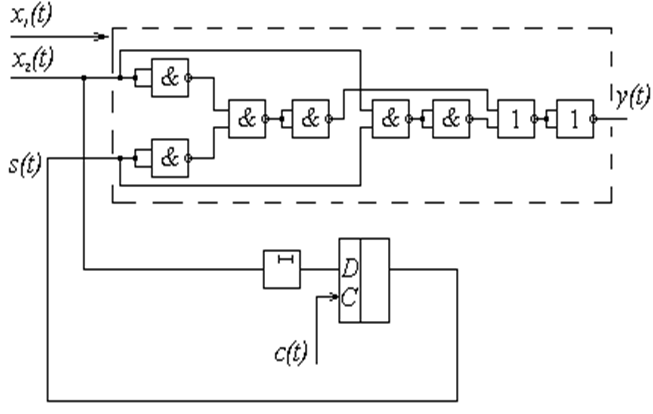
Рисунок 2.3.2 – Схема минимизированного автомата в базисе И – ИЛИ – НЕ
2.3.4 Выводы по разделу
В этом разделе был показан пример минимизации (упрощения) конечного автомата с сокращением числа состояний, а также пример реализации автомата на логических элементах и элементах памяти. Мы убедились в том, что конечный автомат является расширением понятия комбинационной схемы на случай, когда для получения выходного сигнала в данный момент времени требуется “помнить” некоторое количество предыдущих значений входного сигнала, а не только его текущее значение. При практической реализации автомата стала очевидной польза проведённых операций по упрощению исходного автомата и приведению его комбинационной части к конкретному базису.
3 Сети Петри
3.1 Постановка задачи
Для заданной сети Петри, описывающей распределение ресурсов для случая двух процессов, сделать следующее:
а) выписать матричное уравнение смены маркировок;
б) построить дерево и граф покрываемости маркировок;
в) описать поведенческие свойства сети на основе графа покрываемости и матричных уравнений;
г) выписать множество достижимых из μ0 маркировок;
д) разработать программу моделирования сети Петри.
3.2 Теоретические сведения
Сети Петри – наиболее удачный из существующих математический аппарат для моделирования, анализа, синтеза и проектирования самых разных дискретных систем с параллельно протекающими процессами.
Определение. Сетью Петри называется четвёрка элементов
C = (P, T, I ,O), (3.2.1)
где
P = { p1, p2,…,pn }, n > 0 (3.2.2)
множество позиций (конечное),
T = { t1, t2,…,tm }, m > 0 (3.2.3)
множество переходов (конечное),
I: T → P (3.2.4)
функция входов (отображение множества переходов во входные позиции),
O: T → P (3.2.5)
функция выходов (отображение множества переходов в выходные позиции).
Если pi ![]() I (tj)
, то pi – входная позиция
j - го перехода, если pi
I (tj)
, то pi – входная позиция
j - го перехода, если pi
![]() I (tj) , то pi
– выходная позиция j - го перехода.
I (tj) , то pi
– выходная позиция j - го перехода.
Для наглядного представления сетей Петри используются графы.
Граф сети Петри есть двудольный ориентированный мультиграф
G
= (V,![]() ), (3.2.6)
), (3.2.6)
где V = P U T , причём P ∩ T = Ø.
Исходя из графического представления сети Петри, её можно определить и так:
C = (P, T, A), (3.2.7)
где А – матрица инцидентности графа сети.
Определим понятие маркированной сети Петри – оно является ключевым для любой сети.
Маркировка μ сети Петри C = (P, T, I, O) есть функция:
N = μ(P), N ![]() N,
(3.2.8)
N,
(3.2.8)
отображающая множество позиций на множество натуральных чисел. Маркировку можно также определить как вектор:
μ = {μ1, μ2,…, μn} , (3.2.9)
где n =
│P │, а μi ![]() N.
Между этими определениями есть связь:
N.
Между этими определениями есть связь:
μi = μ (pi) (3.2.10)
На графе маркировка отображается ссответствующим числом точек в каждой позиции. Точки называются маркерами или фишками. Если фишек много (больше трёх), то их количество отображается числом.
Таким образом, маркированная сеть Петри представляет собой пятёрку элементов:
M = (P, T, I, O, μ). (3.2.11)
Пример простейшей сети Петри:
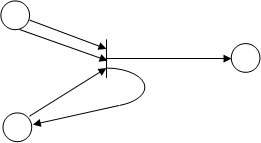 p1
p1
▪▪▪
t1 p3
p2 ▪
Рисунок 3.2.1 – Пример сети Петри
Правила работы с сетями Петри.
Сеть Петри выполняется посредством запуска переходов. Переход может быть запущен в том случае, когда он разрешён. Переход является разрешённым, если каждая из его входных позиций содержит число фишек не меньшее, чем число дуг из неё в данный переход.
Процедура запуска состоит в удалении из каждой входной позиции перехода числа фишек, равного числу дуг из неё, и в выставлении в каждой выходной позиции числа фишек, равного числу дуг, входящему в неё.
Проиллюстрируем сказанное на примере уже нарисованной сети Петри. Запустим в ней переход t1 – он является разрешённым:
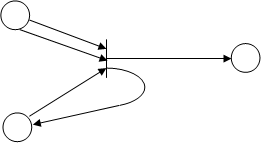 p1
p1
▪
t1 p3
▪
p2 ▪
Рисунок 3.2.2 – Пример запуска перехода сети Петри
Пространство состояний и поведенческие свойства сетей Петри.
Пусть имеется маркированная сеть Петри:
M = (P, T, I, O, μ) (3.2.12)
У неё n позиций. В каждой позиции не более N фишек. Тогда пространство сотояний есть множество всех возможных маркировок сети. Определим δ – функцию следующего состояния.
Если переход tj разрешён при текущей маркировке μ , то следующая маркировка μ’ определится так:
μ’ = δ (μ, tj) (3.2.13)
Если переход tj не разрешён, то δ не определена.
Пусть {tj0, tj1,…, tjs} – последовательность запущенных переходов. Тогда ей будет соответствовать последовательность {μ0, μ1,…,μs+1}, то есть
μk+1 = δ(μk, tjk) (3.2.14)
На основании последнего равенства можно определить
понятие непосредственно достижимой маркировки. Для сети C =
(P, T, I ,O) маркировка μ’
называется непосредственно достижимой из μ , если существует такой
переход tj ![]() T,
при котором
T,
при котором
μ' = δ(μ , tj) (3.2.15)
Можно распространить это понятие на множество достижимых из данной маркировок. Определим множество достижимых из μ маркировок R(C, μ) следующим образом:
во - первых, μ ![]() R(C,
μ);
R(C,
μ);
во - вторых, если μ’ ![]() R(C, μ), μ’ = δ(μ
, tj) и μ’’ = δ(μ’,
tk), то и μ’’
R(C, μ), μ’ = δ(μ
, tj) и μ’’ = δ(μ’,
tk), то и μ’’ ![]() R(C,
μ).
R(C,
μ).
На основе введённых понятий можно сформулировать ряд свойств сети Петри, характеризующих её в процессе смены маркировок – назовём их поведенческими свойствами сети Петри. Определим наиболее важные из них.
1 Достижимость данной маркировки. Пусть имеется некоторая маркировка μ, отличная от начальной. Тогда возникает вопрос достижимости: можно ли путём запуска определённой поледовательности переходов перейти из начальной в заданную маркировку.
2 Ограниченность. Сеть Петри называется k- ограниченной, если при любой маркировке количество фишек в любой из позиций не превышает k. В частности, сеть называется безопасной, если k равно 1. Кроме того, сеть называется однородной, если в ней отсутствуют петли и одинарной (простой), если в ней нет кратных дуг.
3 Активность. Сеть Петри называется активной, если независимо от дотигнутой из μ0 маркировки существует последовательность запусков, приводящая к запуску этого перехода.
Реально
вводят понятия нескольких уровней активности для конкретных переходов. Переход
tj ![]() T называется:
T называется:
а) пассивным (L0- активным), если он никогда не может быть запущен;
б) L1- активным, если он может быть запущен последовательностью переходов из μ0 хотя бы один раз;
в) L2- активным, если для любого числа K существует последовательность запусков переходов из μ0 , при которой данный переход может сработать K и более раз;
г) L3- активным, если он является L2- активным при K → ∞.
4 Обратимость.
Сеть Петри обратима, если для любой маркировки μ ![]() R(C,
μ0) маркировка μ0
достижима из μ.
R(C,
μ0) маркировка μ0
достижима из μ.
5 Покрываемость.
Маркировка μ покрываема, если существует другая маркировка μ’ ![]() R(C, μ0) такая, что в каждой позиции μ’ фишек не меньше, чем в позициях маркировки μ.
R(C, μ0) такая, что в каждой позиции μ’ фишек не меньше, чем в позициях маркировки μ.
6 Устойчивость. Сеть Петри называется устойчивой, если для любых двух разрешённых переходов срабатывание одного из них не приводит к запрещению срабатывания другого.
Существуют два основных метода анализа сетей Петри: матричные и основанные на построении дерева покрываемости.
Первая группа методов основана на матричном
представлении маркировок и последовательностей запуска переходов. Для этого
определим две матрицы размерности количество позиций ![]() количество переходов,
связанные со структурой сети. Первая матрица называется матрицей входов:
количество переходов,
связанные со структурой сети. Первая матрица называется матрицей входов:
D – [i, j] = # (pi , I(tj)), (3.2.16)
каждый её элемент равен числу фишек, уходящих из j- й позиции при запуске i- го перехода. Вторая матрица называется матрицей выходов:
D + [i, j] = # (pi , O(tj)), (3.2.17)
каждый её элемент равен числу фишек, приходящих в j- ю позицию при запуске i- го перехода. Определим единичный вектор e[j] размерности m, содержащий нули во всех позициях кроме той, которая соответствует запускаемому в данный момент переходу. Очевидно, что переход разрешён, если μ ≥ e[j]·D –. Тогда результат запуска j- го перехода можно описать так:
μ’ = μ + e[j]·D, (3.2.18)
где D = (D + – D –) – матрица изменений. Тогда все сформулированные ранее проблемы сети Петри легко интерпретируются матричными уравнениями вида
μ = μ0 + σ·D, (3.2.19)
где μ – исследуемая маркировка, σ – вектор, компоненты которого показывают, сколько раз срабатывает каждый переход.
Хотя данный метод достаточно прост, он не лишён некоторых недостатков. А именно, его применение даёт лишь необходимые условия существования какого- либо свойства, иными словами, может гарантировать лишь его отсутствие, а о присутствии мы сможем говорить с уверенностью, только проанализировав дерево покрываемости (смены) маркировок.
Дерево маркировок сети – это связанный граф, в вершинах которого находятся маркировки, которых мы достигли в результате последовательного запуска разрешённых переходов, а на дугах, соединяющих вершины – зпускаемые переходы. Путь от корня к каждой маркировке отражает последовательность запусков, приведшую к ней. Корнем дерева является начальная маркировка. При неограниченном накапливании фишек в позиции на дереве образуется петля, а в маркировке на месте, соответствующем зациклившейся позиции, ставится ω – символ бесконечно большого числа.
Ясно, что этот метод хотя и требует утомительного перебора всех возможных маркировок сети, но зато по уже готовому дереву достаточно легко анализировать проблемы достижимости, покрываемости, активности, обратимости сети.
Описав поведенческие свойства и методы анализа, можно перейти непосредственно к анализу конкретной сети Петри.
3.3 Расчёты и полученные результаты
Исходная сеть в виде графа:
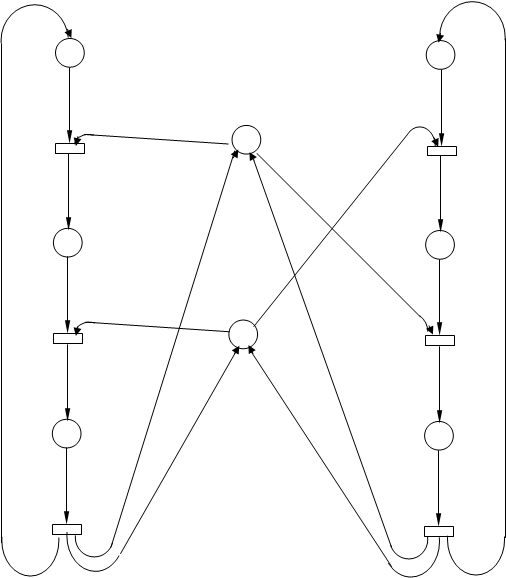
p1 p6
▪ ▪
t1 ▪ p4 t4
p2 p7
t2 ▪ p5 t5
p3 p8
t3 t6
Рисунок 3.3.1 – Исходная сеть Петри
Для матричного анализа сети найдём её матрицу изменений.
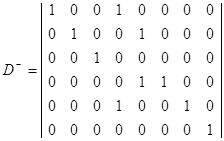 (3.3.1)
(3.3.1)
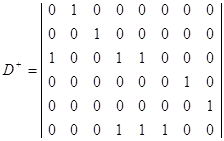 (3.3.2)
(3.3.2)
Матрицу изменений найдём как разность между (3.3.2) и (3.3.1):
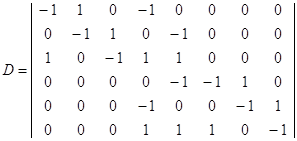 (3.3.3)
(3.3.3)
Таким образом, получив матрицу изменений, можно записать матричное уравнение смены маркировок вида (3.2.19). Вектор начальной маркировки определим так:
μ0 = (10011100) (3.3.4)
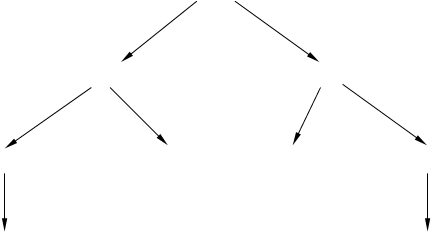
Составим дерево покрываемости маркировок сети.
(10011100) ‘Новая’
t1 t4
‘Новая’ ‘Новая’
(01001100) (10010010)
t2 t4 t1 t5
(00100100) (01000010) (01000010) (10000001)
‘Новая’ ‘Тупик’ ‘Тупик’ ‘Новая’
t3 t6
(10011100) ‘Старая’ (10011100) ‘Старая’
Рисунок 3.3.1 – Дерево покрываемости маркировок
Дерево покрываемости удобно оформить в виде графа. При этом более наглядно видны зацикливающиеся переходы, тупиковые маркировки никакими дополнительными пояснениями снабжать не требуется – отсутствие дуг, исходящих из данной маркировки, говорит само за себя. При достижении старой маркировки её не нужно заново наносить на граф – достаточно соединить дугой предыдущую маркировку и уже существующую “старую”.
Граф покрываемости сети выглядит следующим образом:
μ0
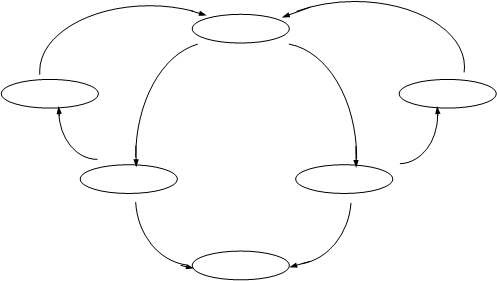 t3
t6
t3
t6
10011100
00100100 t1 t4 10000001
t2 t5
01001100 10010010
t4 t1
01000010
Рисунок 3.3.2 – Граф покрываемости маркировок сети Петри
Проанализируем сеть двумя методами – матричным и графическим и сравним полученные результаты.
Вопрос достижимости какой- либо маркировки легче всего решается, глядя на граф покрываемости. Действительно, возьмём для примера две маркировки: μ1 = (01000010) и μ2 = (00100010). Первая из них достижима, и возможны два пути прихода к ней: t1 , t4 или t4 , t1 . Однако они не единственны, перед вторым запуском перехода возможно бесконечное число раз запустить для первого случая последовательность t2 , t3 , для второго случая – t5 , t6 . Вторая маркировка явно недостижима, так как её нет на графе.
С помощью матриц этот вопрос решается следующим образом. Составляем уравнение вида (3.2.19), в котором вместо σ ставим неизвестный вектор x той же размерности, а вместо μ – интересующую нас маркировку μ1. В итоге получаем систему из 8 уравнений относительно 6 неизвестных компонент вектора x.
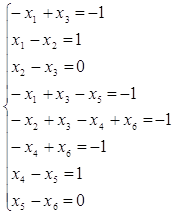 (3.3.5)
(3.3.5)
Проанализировав данную систему, видим, что пятое уравнение является следствием из третьего и шестого, шестое – из седьмого и восьмого, первое – из второго и третьего. Из (1) и (4) следует, что x5 = 0, x6 = 0, из (7) следует, что x4 = 1. Первые три уравнения в (3.3.5) являются линейно зависимыми, поэтому за свободное неизвестное примем x1. Тогда получаем решение в виде x1 = {y y-1 y-1 1 0 0}, где y – любое целое число. Полученное решение говорит о достижимости маркировки μ1 и указывает, какие из переходов и сколько раз должны быть для этого запущены.
Сравнив оба способа решения, сразу можно увидеть недостатки второго. Во- первых, решение (3.3.5) не указывает, в какой именно последовательности должны быть запущены указанные переходы. Во- вторых, глядя на матрицу изменений, мы не можем судить о наличии в сети петель. Кроме того, полученное матричное решение не даёт, вообще говоря, гарантий своей реализуемости – оно является лишь необходимым условием достижимости. Однако, не получив решения, можно говорить о недостижимости маркировки.
Действительно, записав (3.2.19) для μ2, получаем систему:
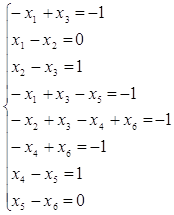 (3.3.6)
(3.3.6)
Система является несовместной, так как после вычитания третьего уравнения из шестого получаем уравнение, противоречащее пятому. Поэтому можно сделать вывод о недостижимости μ2, совпадающий с полученным из графа покрываемости маркировок.
Исходя из графа (3.3.2), можно заключить, что сеть является безопасной. Действительно, ни в одной из позиций на маркировках не накапливается больше одной фишки. Это говорит о том, что реальный процесс, описываемый сетью, протекает без конфликтов. Однако о полном отсутствии конфликтов говорить пока рано. Данный вывод невозможно получить из матричного уравнения, так как он является обобщением, сделанным на основе знания всех возможных маркировок, получающихся в сети.
Данная сеть является активной – в ней каждый переход может сработать хотя бы один раз. Проанализируем уровни активности отдельных переходов. Переходы t1 и t4 являются L1- активными, так как они в худшем случае (то есть при получения тупиковой маркировки) могут сработать хотя бы один раз. Переходы t2, t3, t5 и t6 являются L2- активными, так как они могут сработать любое наперёд заданное число раз и даже больше.
Отсюда можно сделать вывод о том, что данная сеть не является бесконфликтной – у неё есть тупиковое состояние.
Можно также сказать, что сеть является обратимой. Этот вывод можно получить и матричным путём – решив уравнение
x·D = 0 (3.3.7)
Получаем систему
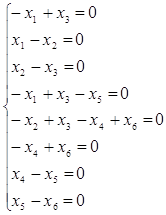 (3.3.8)
(3.3.8)
Данная система имеет 2 решения: {y y y 0 0 0} и {0 0 0 y y y}, где y – любое. Действительно, запуская любое число раз последовательности t1 t2 t3 или t4 t5 t6 , каждый раз мы возвращаемся к исходной маркировке.
Из графа (3.3.2) также следует, что ни одна из маркировок сети не является покрываемой. Действительно, ни для одной маркировки не существует другой такой, для которой в каждой позиции было бы не меньше фишек, чем в исходной.
Можно сказать, что данная сеть не является устойчивой. У неё есть тупик, и, кроме того, непосредственно перед переходом в тупиковое состояние всегда существуют два разрешённых перехода. Запуская ‘неправильный’ переход, мы запрещаем оба – и оказываемся в тупике. Такое свойство сети говорит о наличии потенциально возможных конфликтов.
Па основании графа (3.3.2) можно выписать множество достижимых из μ0 маркировок:
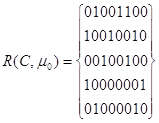 (3.3.9)
(3.3.9)
Для моделирования сети была написана программа на языке Turbo Pascal. Она отображает состояние сети и разрешённые в каждый момент переходы. Для выбора запускаемого перехода используется мышь.
3.4 Выводы по разделу
В данном разделе быа проанализирована и смоделирована сеть Петри, которая служит моделью функционирования двух производственных процессов, связанных двумя общими ресурсами. В результате можно сделать вывод о принципиальном наличии в системе тупиковой ситуации, которая возникает при попытке одновременного запуска обоих процессов на выполнение. Чтобы не возникало тупика, необходимо каждый из процессов доводить до завершения, и не запускать другой процесс, пока не окончены все три цикла первого. Всё вышесказанное полностью подтверждается написанной программой, моделирующей все описанные ситуации, возникающие в сети.
ЗАКЛЮЧЕНИЕ
В работе были рассмотрены вопросы упрощения и синтеза дискретных двоичных устройств с ‘памятью’ и без неё, а также проанализирована сеть Петри, моделирующая конкретный производственный процесс и сделаны соответствующие выводы относительно самого процесса.
ЛИТЕРАТУРА
1 Сигорский В.П. Математический аппарат инженера.– Киев:Техника, 1975. –538 с.
2 Г.Корн, Т.Корн Справочник по математике для научных работников и инженеров.– М.: Наука, 1984. –831 с.
3 В.Брауэр Введение в теорию конечных автоматов.– М.: Радио и связь, 1987. –392 с.
4 Фаронов В.В. Турбо Паскаль 7.0: практика программирования. – М.: Нолидж, 1997. –432 с.
Приложение А
Программа моделирования сети Петри
Program Farewell_Pascal_Please_Forgive_Me;
Uses graph,crt;
Const m_0=$9C;
r_0=$90;
path='cursor.dat';
mask:array[0..5] of byte = ($90,$48,$20,$0C,$12,$01);
jump:array[0..5] of word = ($406F,$20B7,$98DF,$02F3,$01ED,$1CFE);
Var
i,j,counter,number:integer;
flag_of_exit:boolean;
ok:word;
bm:integer;
ScrMask:array[1..64] of byte;
r,m,old_m,old_r:byte;
f:file of byte;
procedure Init_Graph_Mode;
var
Driver,
Mode,
ErrCode: Integer;
begin
Driver := Detect;
InitGraph(Driver, Mode, '');
ErrCode := GraphResult;
if ErrCode <> grOk then
begin
Writeln('Ошибка графического режима:',
GraphErrorMSG(ErrCode));
Halt(1);
end;
SetTextStyle(DefaultFont, HorizDir, 1);
SetColor(15);
SetLineStyle(0,0,1);
SetFillStyle(1,0)
end;
function Init_Mouse:word;
begin
asm
push ax
mov ax,00h
int 33h
mov @Result,ax
pop ax
end
end;
procedure Show_Mouse;
begin
asm
push ax
mov ax,01h
int 33h
pop ax
end
end;
procedure Hide_Mouse;
begin
asm
push ax
mov ax,02h
int 33h
pop ax
end
end;
procedure Set_Graph_Cursor(segm,ofst:word;x,y:integer);
begin
asm
push ax
push bx
push cx
push dx
mov bx,x
mov cx,y
mov es,segm
mov dx,ofst
mov ax,09h
int 33h
pop dx
pop cx
pop bx
pop ax
end
end;
procedure Get_Mouse_State(var bt,x,y:integer);
begin
asm
push ax
push bx
push cx
push dx
mov ax,03h
int 33h
lds di,bt
mov [di],bx
lds di,x
mov [di],cx
lds di,y
mov [di],dx
pop dx
pop cx
pop bx
pop ax
end
end;
procedure Get_Web_State;
begin
r := 0;
for counter:= 0 to 5 do
if (mask[counter] and m) = mask[counter] then
r := r or ($80 shr counter)
end;
procedure Design_Kernel;
begin
OutTextXY(190,20,'Распределение ресурсов для');
OutTextXY(207,27,'случая двух процессов');
for counter := 0 to 2 do
Circle(150,counter*150+50,15);
for counter := 0 to 2 do
Circle(450,counter*150+50,15);
for counter := 0 to 1 do
Circle(300,counter*150+120,15);
for counter := 0 to 2 do
begin
Line(140,counter*150+123,160,counter*150+123);
Line(140,counter*150+127,160,counter*150+127);
Line(140,counter*150+123,140,counter*150+127);
Line(160,counter*150+123,160,counter*150+127)
end;
for counter := 0 to 2 do
begin
Line(440,counter*150+123,460,counter*150+123);
Line(440,counter*150+127,460,counter*150+127);
Line(440,counter*150+123,440,counter*150+127);
Line(460,counter*150+123,460,counter*150+127)
end;
for counter := 0 to 1 do
begin
Line(counter*300+150,65,counter*300+150,123);
Line(counter*300+150,127,counter*300+150,185);
Line(counter*300+150,215,counter*300+150,273);
Line(counter*300+150,277,counter*300+150,335);
Line(counter*300+150,365,counter*300+150,423);
Line(counter*300+150,123,counter*300+148,114);
Line(counter*300+150,123,counter*300+152,114);
Line(counter*300+150,185,counter*300+148,176);
Line(counter*300+150,185,counter*300+152,176);
Line(counter*300+150,273,counter*300+148,264);
Line(counter*300+150,273,counter*300+152,264);
Line(counter*300+150,335,counter*300+148,326);
Line(counter*300+150,335,counter*300+152,326);
Line(counter*300+150,423,counter*300+148,414);
Line(counter*300+150,423,counter*300+152,414)
end;
Arc(120,427,180,360,25);Arc(480,427,180,360,25);
Arc(122,35,0,180,27);Arc(478,35,0,180,27);
Line(95,35,95,425);Line(505,35,505,425);
Line(293,134,163,431);Arc(159,427,180,330,5);
Line(290,281,170,436);Arc(162,427,180,320,12);
Line(307,134,436,431);Arc(440,427,210,360,5);
Line(310,281,429,436);Arc(438,427,220,360,12);
Line(283,117,169,106);Arc(171,121,80,180,15);
Line(312,129,439,262);Arc(429,273,0,45,15);
Line(283,267,169,256);Arc(171,271,80,180,15);
Line(311,257,426,110);Arc(432,121,0,160,12);
Line(150,35,145,26);Line(150,35,150,26);
Line(450,35,455,26);Line(450,35,450,26);
Line(155,123,156,114);Line(155,123,159,115);
Line(155,273,156,264);Line(155,273,159,265);
Line(445,123,444,114);Line(445,123,440,115);
Line(445,123,444,114);Line(445,123,441,116);
Line(445,273,444,264);Line(445,273,440,265);
Line(293,135,287,142);Line(293,135,291,143);
Line(307,135,309,143);Line(307,135,312,142);
Line(290,282,282,288);Line(290,282,285,290);
Line(311,282,315,290);Line(311,282,317,288);
SetFillStyle(1,8);
for counter := 0 to 1 do
begin
Line(540,counter*70+150,600,counter*70+150);
Line(540,counter*70+170,600,counter*70+170);
Line(600,counter*70+150,600,counter*70+170);
Line(540,counter*70+150,540,counter*70+170);
FloodFill(570,counter*70+160,15)
end;
SetFillStyle(1,15);
OutTextXY(543,159,'Restore');
OutTextXY(555,229,'Exit');
end;
procedure Design_Mark_and_Jumps;
begin
SetColor(15);
SetLineStyle(0,0,3);
SetFillStyle(1,15);
Hide_Mouse;
for counter := 0 to 2 do
if ((m shr (7 - counter)) and 1) = 1 then
begin
SetColor(15);
SetFillStyle(1,15);
FillEllipse(150,counter*150+50,1,1)
end
else
begin
SetColor(0);
SetFillStyle(1,0);
FillEllipse(150,counter*150+50,1,1)
end;
for counter := 3 to 4 do
if ((m shr (7 - counter)) and 1) = 1 then
begin
SetColor(15);
SetFillStyle(1,15);
FillEllipse(300,(counter-3)*150+120,1,1)
end
else
begin
SetColor(0);
SetFillStyle(1,0);
FillEllipse(300,(counter-3)*150+120,1,1)
end;
for counter := 5 to 7 do
if ((m shr (7 - counter)) and 1) = 1 then
begin
SetColor(15);
SetFillStyle(1,15);
FillEllipse(450,(counter-5)*150+50,1,1)
end
else
begin
SetColor(0);
SetFillStyle(1,0);
FillEllipse(450,(counter-5)*150+50,1,1)
end;
for counter := 0 to 2 do
if ((r shr (7 - counter)) and 1) = 1 then
begin
SetFillStyle(1,10);
FloodFill(150,counter*150+125,15)
end
else
begin
SetFillStyle(1,12);
FloodFill(150,counter*150+125,15)
end;
for counter := 3 to 5 do
if ((r shr (7 - counter)) and 1) = 1 then
begin
SetFillStyle(1,10);
FloodFill(450,(counter-3)*150+125,15)
end
else
begin
SetFillStyle(1,12);
FloodFill(450,(counter-3)*150+125,15)
end;
SetColor(15);
SetFillStyle(1,15);
Show_Mouse
end;
Begin
Init_Graph_Mode;
ok := Init_Mouse;
flag_of_exit := false;
m := m_0;
r := r_0;
old_m := 0;
old_r := 0;
if ok = $FFFF then
begin
{$I-} assign(f,path);
reset(f);
ok := filesize(f);
{$I+} if (IOResult = 0) and (ok = 64) then
begin
for i := 0 to 63 do
read(f,ScrMask[i]);
Set_Graph_Cursor(seg(ScrMask),ofs(ScrMask),2,2)
end;
Design_Kernel;
Show_Mouse;
repeat
Get_Mouse_State(bm,i,j);
if (m <> old_m) or (r <> old_r) then
begin
Get_Web_State;
Design_Mark_and_Jumps;
old_m := m;
old_r := r
end;
if bm = 1 then
begin
number := 6;
for counter := 0 to 2 do
if (i < 165) and (i > 135) and
(j < counter*150+130) and (j > counter*150+120)
then
number := counter;
for counter := 3 to 5 do
if (i < 465) and (i > 435) and
(j < (counter-3)*150+130) and (j > (counter-3)*150+120)
then
number := counter;
if (number < 6) and (((1 shl (7-number)) and r) <> 0) then
begin
m := m and (jump[number] and $FF);
m := m or (jump[number] shr 8)
end;
if (i < 600) and (i > 540) and (j < 170) and (j > 150)
then
m := m_0;
if (i < 600) and (i > 540) and (j < 240) and (j > 220)
then
flag_of_exit := true
end;
until flag_of_exit;
Hide_Mouse;
CloseGraph
end
else
begin
CloseGraph;
WriteLn('Ошибка мыши: Device or driver not found.')
end
End.