
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология и педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по информатике программированию
Краткое содержание произведений
Реферат: Расчет затвердевания плоской отливки
Реферат: Расчет затвердевания плоской отливки
Министерство образования Российской Федерации
Сибирский государственный индустриальный университет
Кафедра литейного производства
Расчет затвердевания плоской отливки
в массивной форме
Выполнили: ст. гр. МЛА-97
Злобина С. А.
Карпинский А. В.
Кирина Л. В.
Тимаревский А. В.
Токар А. Н.
Проверил: доцент, к.т.н.
Передернин Л.В.
Новокузнецк 2001
СодержаниеСодержание. 2
Задание. 3
Постановка задачи. 4
1. Графическое представление. 4
2. Математическая формулировка задачи. 5
Метод расчета. 7
Схема апроксимации. 8
Алгоритм расчета. 11
Идентификаторы.. 13
Блок-схема. 14
Программа. 17
Сравнение с инженерными методами расчета. 20
Результаты расчета. 21
ЗаданиеОтливка в виде бесконечной плиты толщиной 2Lo=30 мм
Сплав: Латунь (10% Zn).
Форма: Песчано-глинистая объемная сырая (ПГФ).
Индексы: 1-Метв, 2- Меж, 4-форма.
а1=3,6×10-5 м2/с
а2=2,1×10-5 м2/с
l1=195 Вт/м×К
l2=101 Вт/м×К
r1=8600 кг/м3
r2=8000 кг/м3
L=221000 Дж/кг
b4=1300 Вт×с1/2/(м2×К)
Tф=293 К
Ts=1312,5 К
Tн=1345 К
N=100
et=0,01 c
eТ=0,01 oC
Постановка задачи1.
 |
Графическое представление
Принимаем следующие условия:
Отливка в виде бесконечной плиты толщиной 2Lo затвердевает в объемной массивной песчано-глинистой форме. Принимаем, что теплофизические характеристики формы и металла постоянны и одинаковы по всему объему, системы сосредоточенные, геометрическая ось совпадает тепловой и поэтому можно рассматривать только половину отливки. Lo<<Lф - форма массивная, т.е. форма за все время охлаждения не прогревается до конца, Тпов=Тнач; такая форма называется бесконечной
Вектор плотности теплового потока (удельный тепловой поток) имеет направление перпендикулярное к поверхности раздела отливка-форма в любой момент времени tk;
Нестационарное температурное поле – одномерное, Тj(х, tk), j=1,2,4;
Температура затвердевания принимается постоянной, равной Ts;
Теплофизические характеристики сред, aj=lj/cjrj, j=1,2,4;
Теплоаккумулирующую способность формы
примем постоянной, bф=![]() =const;
=const;
C,l,r - теплофизические характеристики формы;
Переохлаждение не учитываем;
Удельная теплота кристаллизации L(Дж/кг) выделяется только на фронте затвердевания (nf) - условие Стефана;
Не учитывается диффузия химических элементов – квазиравновесное условие;
Перенос тепла за счет теплопроводности и конвекции учитывается введением коэффициента эффективной электропроводности:
для жидкой среды l2=n*l0, где l0 – теплопроводность неподвижного жидкого металла; n=10;
Не учитывается усадка металла при переходе из жидкого состояния в твердое;
Передача тепла в жидком и твердом металле происходит за счет теплопроводности и описывается законом Фурье:
q = - ljgradT, плотность теплового потока,![]() Дж/(м2с);
Дж/(м2с);
Отливка и форма имеют плотный контакт в период всего процесса затвердевания (что реально для ПГФ);
теплоотдача на границе отливка – форма
подчиняется закону Ньютона(-Рихтмона): q1(tk)=a(T1к - Tф)
– для каждого момента времени tк, где a - коэффициент теплоотдачи, для
установившегося режима (автомодельного) a=![]() ;
;
Полученная таким образом содержательная модель и ее графическая интерпретация затвердевания плоской отливки в объемной массивной форме, упрощает формулировку математической модели и достаточно хорошо отражает затвердевание на тепловом уровне, т.е. позволяет получить закон T=f(x;t).
2. Математическая формулировка задачи
Математическая модель формулируется в виде краевой задачи, которая включает следующие положения:
а) Математическое выражение уравнения распределения теплоты в изучаемых средах.
Дифференциальное уравнение теплопроводности Фурье, которое имеет смысл связи, между временным изменением температуры и ее пространственным распределением:
![]()
Или в соответствии с условием 5 запишем:
![]() ; xÌ[0,lo],
j=
; xÌ[0,lo],
j=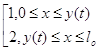 (1)
(1)
б) Условия однозначности:
1. Теплофизические характеристики сред
rj, lj, cj, bj, aj, TL, TS
2. Начальные условия
2.1 Считаем, что заливка происходит мгновенно и мгновенно же образуется тончайшая корка твердого металла.
T1н(x, tн)= TS(E) (2)
2.2 Положение фронта затвердевания
t=tнзадан. ,x=0, y(tн)=0 (3)
2.3 Температура металла в отливке
Tj,iн=Tн ; j=2, iÌ(2,n) (4)
2.4 Температура на внешней поверхности формы (контакт форма - атмосфера) и температура формы.
T4н=Tф (5)
3. Граничные условия
3.1 Условия сопряжения на фронте затвердевания (условия Стефана) i=nf
![]() (6)
(6)
3.2 Температура на фронте затвердевания
![]()
![]() (7)
(7)
3.3 Условие теплоотдачи на границе отливка-форма
![]()
![]() (8)
(8)
- граничное условие третьего рода
3.4 Условие на оси симметрии
![]() (9)
(9)
Задача, сформулированная в выражениях (1-9) есть краевая задача, которая решается численным методом.
Аппроксимировав на сетке методом конечных разностей (МКР), получим дискретное сеточное решение.
Ti=f(xi;tk).
Метод расчетаБудем использовать МКР – метод конечных разностей.
Сформулированную краевую задачу дискретизируем на сетке.
![]()
![]()
![]() =
=![]() - шаг по пространству
постоянный;
- шаг по пространству
постоянный;![]() - шаг по времени переменный
- шаг по времени переменный
Для аппроксимации задачи на выбранной сетке можно использовать разные методы – шаблоны. Наиболее известные из них для данного типа задач четырех точечный конечно разностный шаблон явный и неявный.
Явный четырех точечный шаблон Неявный четырех точечный шаблон
 |
Использование явного шаблона для каждого временного шага получаем n+1 уравнение с n неизвестными и система решается методом Гауса, но сходимость решения только при очень малых шагах.
Использование неявного шаблона обеспечивает абсолютную сходимость, но каждое из уравнений имеет 3 неизвестных, обычным методом их решить невозможно.
По явному:
![]() (10)
(10)
По неявному:
![]() (11)
(11)
Сходимость обеспечивается при:
![]() при явном шаблоне (12)
при явном шаблоне (12)
![]() -точность
аппроксимации
-точность
аппроксимации
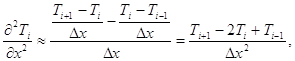 (13)
(13)
Аппроксимируем задачу 1-9 на четырех точечном неявном шаблоне
Начальные условия:
![]() (14)
(14)
![]() (15)
(15)
![]()
![]() (16)
(16)
![]()
![]() (17)
(17)
![]() (18)
(18)
Граничные условия:
![]() (19)
(19)
![]() (20)
(20)
![]() (21
a)
(21
a)
![]() =>
=> ![]() (21)
(21)
Условие идеального контакта на границе отливка форма
![]() (22)
(22)
Расчет временного шага ![]() :
:
Величина ![]() -var рассчитывается из условия, что за промежуток времени
-var рассчитывается из условия, что за промежуток времени ![]() фронт перейдет из точки nf в точку nf+1
фронт перейдет из точки nf в точку nf+1
Расчет ведут итерационными (пошаговыми) методами
Строим процедуру расчета следующим образом:
Вычисляем нулевое приближенное ![]() для каждого шага,
для каждого шага,
За шаг итерации примем S,
Нулевое приближение S=0.
![]() (23)
(23)
Уточняем шаг: S+1
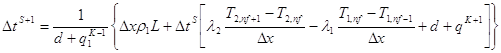 (24)
(24)
d – параметр итерации от 0 до 1
для расчета возьмем d=0.
Число S итераций определяется заданной точностью:
Временного шага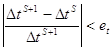 (25)
(25)
И по температуре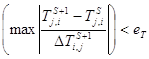 (26)
(26)
et и eT – заданные точности по времени и температуре
et=0,01c, eT=0,1°C
DtI=0,01c – время за которое образовалась корочка.
Описанный итерационный процесс называют ''Ловлей фазового фронта в узел''.
Можно задать Dх, DtK=const, тогда неизвестно будет положение фронта, при помощи линейной интерполяции.
Расчет температурных полей:
Метод «прогонки»:
Считается наиболее эффективным для неявно заданных конечно-разностных задач.
Суть метода:
Запишем в общем виде неявно заданное конечноразностное уравнение второго порядка (14) в общем виде:
AiTi-1 – BiTi + CiTi+1 + Di = 0 ; i = 2, 3, 4, …n-1 (27)
действительно для всех j и k.
и краевые условия для него:
T1 = p2T2 + q2 (28 а)
Tn = pnTm-1 + qn (28 б)
Ti = f(Ai; Xi; tk) - сеточное решение.
Ai, Bi, Ci, Di – известные коэффициенты, определенные их условий однозначности и дискретизации задачи.
Решение уравнения (27) – ищем в том же виде, в котором задано краевое условие (28 а)
Ti = аi+1Ti+1 + bi+1 ; i = 2, 3, 4, …n-1 (29)
Ai+1, bi+1 – пока не определенные «прогоночные» коэффициенты (или коэффициенты разностной факторизации)
Запишем уравнение (29) с шагом назад:
Ti-1 = аiTi + bi (30)
Подставим уравнение (30) в уравнение (27):
Ai(aiTi + bi) – BiTi + CiTi+1 + Di = 0
Решение нужно получить в виде (29):
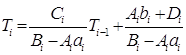 (31)
(31)
Найдем метод расчета прогоночных коэффициентов.
Сравним уравнение (29) и (31):
![]() (32)
(32)
![]() (33)
(33)
(32),(33)– рекуррентные прогоночные отношения позволяющие вычислить прогоночные коэффициенты точке (i+1) если известны их значения в точке i.
Процедура определения коэффициентов аi+1 и bi+1 называется прямой прогонкой или прогонкой вперед.
Зная коэффициенты конечных точек и температуру в конечной точке Тi+1 можно вычислить все Тi.
Процедура расчета температур называется обратной прогонкой. То есть, чтобы вычислить все Т поля для любого tk нужно вычислить процедуры прямой и обратной прогонки.
Чтобы определить начальные а2и b2, сравним уравнение (29) и уравнение (28 а):
a2 = p2; b2 = q2
Запишем уравнение 29 с шагом назад:
![]() Tn = pnTn-1 + qn
Tn = pnTn-1 + qn
Tn-1 = qnTn + bn
![]() (34)
(34)
Новая задача определить pn , qn
Вывод расчетных формул:
Преобразуем конечноразностное уравнение (14) в виде (27)
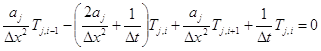 , j=1,2 (35)
, j=1,2 (35)
относиться к моменту времени k
Из (35)
=> Ai=Ci=![]() Bi=2Ai+
Bi=2Ai+![]() Di=
Di=![]() (36)
(36)
Определим значения коэффициентов для граничных условий:
на границе раздела отливка-форма
![]() (37)
(37)
приведем это выражение к виду (28 а)
![]() отсюда (38)
отсюда (38)
b2=q2=![]() a2=p2=1
(39)
a2=p2=1
(39)
на границе раздела Meтв - Меж
из (29), Tnf=Tn=> anf+1=0, bnf+1=Ts (40)
условие на оси симметрии
Tn-1=Tn в соответствии с (21)
pn=1, qn=0 (41)
подставив (41) в (34) получим
![]() (42)
(42)
1) Определить теплофизические характеристики сред, участвующих в тепловом взаимодействии λ1, λ2, ρ1, ρ2, L, а1, а2, Тs, Тн, Тф.
2) Определить размеры отливки, параметры дискретизации и точность расчета
2l0=30 мм, l0=R=15 мм=0,015 м
n=100,
![]()
первый шаг по времени: Δt1=0,01 с, t=t+Δt
еt=0,01 с, et=0,1 оC
3) Принять, что на первом временном шаге к=1, t1=Δt1, nf=1, Т1=Т3, Тi=Тн, , i=2,…,n, Т4=Тф
4) Величина плотности теплового потока на границе раздела отливка – форма
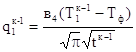 (43)
(43)
![]() , s=0,
(нулевое приближение)
, s=0,
(нулевое приближение)
к=2, ![]() (44)
(44)
5) Найти нулевое приближение Δtк, 0 на к-том шаге
переход nf → i → i+1 по формуле (23)
![]()
6) Найти коэффициенты Ai, Сi, Вi, Di по соответствующим формулам для сред Метв. и Меж. В нулевом приближении при s=0
7) Рассчитать прогоночные коэффициенты ai+1, bi+1 для Метв. и Меж., s=0 с учетом что Тnf=Тз.
Т1=р2Т2+g2
Тi=а2Т2+в2
Найти а2 и в2:
а2=1,
![]() (45)
(45)
![]() (46)
(46)
![]()
8) Рассчитать температуру на оси симметрии
![]() (47)
(47)
![]()
9) Рассчитать температурное поле жидкого и твердого металла
![]() (48)
(48)
10) Пересчитать значения ∆tк по итерационному процессу (24)
![]()
d – параметр итерации (d=0…1)
проверяем точность;
11) Скорость охлаждения в каждом узле i рассчитать по формуле:
![]() ,
оС/с (50)
,
оС/с (50)
12) Скорость затвердевания на каждом временном шаге:
![]() ,
м/с (51)
,
м/с (51)
13) Средняя скорость охлаждения на оси отливки:
![]()
14) Положение фронта затвердевания по отношению к поверхности отливки
![]() ,
к – шаг по времени (52)
,
к – шаг по времени (52)
15) Полное время затвердевания
![]() ,
к′ - последний шаг (53)
,
к′ - последний шаг (53)
16) Средняя скорость затвердевания отливки
![]() (54)
(54)
|
|
|||
|
|
|||
|
|
|
||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
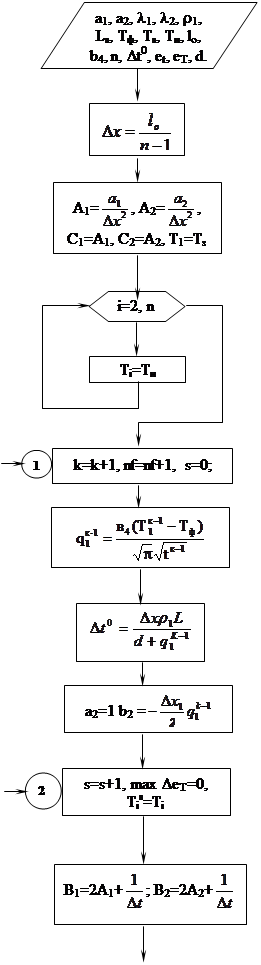 Блок-схема
Блок-схема
- [Вводим исходные данные
- [Вычисляем шаг по пространству
- [Вычисляем коэффициенты Аj, Сj для подстановки в (32), (33) и задаем температуру в первой точке
![]() -
[Температурное поле для первого шага по времени
-
[Температурное поле для первого шага по времени
![]() - [Делаем шаг
по времени
- [Делаем шаг
по времени
- [Вычисляем плотность теплового потока
- [Шаг по времени в нулевом приближении
- [Начальные прогоночные коэффициенты
- [Шаг по итерации
- [Вычисляем коэффициенты Bj для подстановки в (32), (33)

- [Вычисляем прогоночные коэффициенты по твердому металлу
- [Прогоночные коэффициенты для фронта
- [Вычисляем прогоночные коэффициенты по жидкому металлу
- [Температура на оси симметрии
- [Расчет температурного поля
- [Ищем максимальный температурный шаг
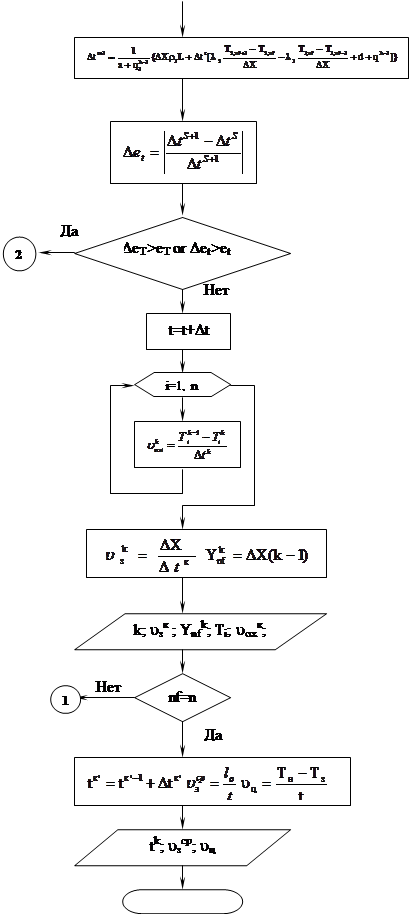
- [Уточняем Dt
- [Точность временного шага
- [Проверка точности
- [Расчет времени
- [Скорость охлаждения в каждом узле
- [Скорость затвердевания и положение фронта
- [Вывод результатов
- [Проверка достижения фронтом центра отливки
- [Расчет полного времени, ср. скорости затвердевания ср. скорости охлаждения на оси отливки
Вывод результатов
- [Конец.
ПрограммаCLEAR , , 2000
DIM T(1000), T1(1000), AP(1000), BP(1000), Vox(1000), N$(50)
2 CLS
N = 100: KV = 50: N9 = 5: L = .015
TM = 293: TI = 1345: TS = 1312.5
BM = 1300: a1 = .000036: a2 = .000021
TA0 = .01: ETA = .01: E = .01
l1 = 195: l2 = 101
R0 = 8600: LS = 221000
AF = 0: Pi = 3.14159265359#
3 PRINT "Число шагов N, штук"; N
PRINT "Длина отливки L, м"; L
PRINT "Температура формы Tf, К"; TM
PRINT "Начальная температура сплава Tн, К"; TI
PRINT "Температура затвердевания Tz, К"; TS
PRINT "Bф "; BM
PRINT "Первый шаг по времени, Tk0 "; TA0
PRINT "Точность по времени, Еt "; ETA
PRINT "Точность по температуре, ЕТ "; E
PRINT "Температуропроводность Ме твердого, а1 "; a1
PRINT "Температуропроводность Ме жидкого, а2 "; a2
PRINT "LS= "; LS
PRINT "Коэф. теплопроводности, l1 "; l1
PRINT "Коэф. теплопроводности, l2"; l2
PRINT "Плотность Ме твердого, р1 "; R0
INPUT "Изменить данные <y/n>"; QV$
IF QV$ = "Y" THEN GOSUB 222
48 N1 = N - 1
DX = L / (N - 1)
A = a1 / DX ^ 2
B1 = 2 * A
RL = R0 * LS * DX
NF = 1
B2 = l1 / DX
KV1 = 1
AL = a2 / DX ^ 2
BL1 = 2 * AL
BL2 = l2 / DX
T(1) = TS
T1(1) = TS
FOR i = 2 TO N
T(i) = TI
T1(i) = TI
NEXT i
TA = TA0
K = 1
dta = .01
GOTO 103
101 K = K + 1
NF = NF + 1
B3 = SQR(Pi * TA)
q = BM * (T(1) - TM) / B3
dta = RL / (AF + q)
B5 = BM * TM / B3
B3 = BM / B3
B4 = B2 + B3
AP(1) = B2 / B4
BP(1) = B5 / B4
T(NF) = TS
NF1 = NF - 1
NF2 = NF + 1
K1 = 0
102 K1 = K1 + 1
Et = 0
B3 = SQR(Pi * (TA + dta))
q = BM * (T(1) - TM) / B3
B5 = BM * TM / B3
B3 = BM / B3
B4 = B2 + B3
AP(1) = B2 / B4
BP(1) = B5 / B4
DTA1 = 1 / dta
IF NF1 = 1 THEN GOTO 23
FOR i = 2 TO NF1
B = B1 + DTA1
f = DTA1 * T1(i)
B4 = B - A * AP(i - 1)
AP(i) = A / B4
BP(i) = (A * BP(i - 1) + f) / B4
NEXT i
23 FOR i = NF1 TO 1 STEP -1
TC = AP(i) * T(i + 1) + BP(i)
B = ABS(TC - T(i)) / TC
IF B > Et THEN Et = B
T(i) = TC
NEXT i
AP(NF) = 0
BP(NF) = TS
B = BL1 + DTA1
FOR i = NF2 TO N
f = DTA1 * T1(i)
B4 = B - AL * AP(i - 1)
AP(i) = AL / B4
BP(i) = (AL * BP(i - 1) + f) / B4
NEXT i
IF NF = N THEN GOTO 34
TC = BP(N) / (1 - AP(N))
B = ABS(TC - T(N)) / TC
T(N) = TC
IF B > Et THEN Et = B
IF NF >= N1 THEN GOTO 34
FOR i = N1 TO NF2 STEP -1
TC = AP(i) * T(i + 1) + BP(i)
B = ABS(TC - T(i)) / TC
IF B > Et THEN Et = B
T(i) = TC
NEXT i
34 P = AF + q
P1 = 1 / P
TM2 = BL2 * (T(NF2) - TS)
IF NF = N THEN GOTO 80
TM1 = B2 * (TS - T(NF1))
DTF = P1 * (RL + dta * (TM2 - TM1 + P))
P3 = ABS(DTF - dta) / DTF
dta = DTF
IF (P3 > ETA) OR (Et > E) THEN GOTO 102
80 TA = TA + dta
IF NF = 1 THEN dta = TA0
Vox = (T1(NF) - TS) / dta
FOR i = 1 TO N
Vox(i) = (T1(i) - T(i)) / dta
T1(i) = T(i)
NEXT i
VS = DX / dta
Xf = (K - 1) * DX
IF K <> KV1 + 1 THEN GOTO 33
KV1 = KV1 + KV
GOSUB 777
33 GOTO 105
103 PRINT "РЕЗУЛЬТАТЫ РАСЧЕТА": CLS : GOSUB 777
105 IF K < N THEN GOTO 101
GOSUB 777
Vz = 1000 * L / TA
Voxl = (TI - TS) / TA
PRINT "Полное время затв. отл. TA="; TA; "с."
PRINT "Ср. скорость охл. на оси отл. Voxl="; Voxl; " K/с"
PRINT "Ср. скорость затв. отл. Vz="; Vz; " мм/с"
END
777 PRINT "К="; K; " DTA="; dta; "VS="; VS * 1000; " мм/с XF="; Xf; " мм"
PRINT "T="; T(1); : FOR i = 1 TO 10: PRINT T(i * 10); : NEXT i: PRINT "K"
PRINT "Vox="; Vox(1); : FOR i = 1 TO 10: PRINT Vox(i * 10); : NEXT i: PRINT "K/c"
RETURN
222 CLS
INPUT "Число шагов N, штук"; N
INPUT "Длина отливки L, м"; L
INPUT "Температура формы Tf, К"; TM
INPUT "Начальная температура сплава Tн, К"; TI
INPUT "Температура затвердевания Tz, К"; TS
INPUT "Bф "; BM
INPUT "Первый шаг по времени, Tk0 "; TA0
INPUT "Точность по времени, Еt "; ETA
INPUT "Точность по температуре, ЕТ "; E
INPUT "Температуропроводность Ме твердого, а1 "; a1
INPUT "Температуропроводность Ме жидкого, а2 "; a2
INPUT "LS= "; LS
INPUT "Коэф. теплопроводности, l1 "; l1
INPUT "Коэф. теплопроводности, l2"; l2
INPUT "Плотность Ме твердого, р1 "; R0
CLS
GOTO 3
RETURN
Сравнение с инженерными методами расчетаГ. Ф. Баландин для расчета продолжительности затвердевания отливки эвтектического сплава предложил следующие выражения:
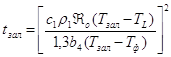 -время
заливки
-время
заливки
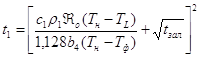 -время
снятия перегрева
-время
снятия перегрева
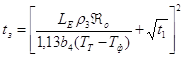 -время
затвердевания
-время
затвердевания
Принимаем Tзал=TL+70, Тн=1/2(Tзал+ТL)
Расчет:
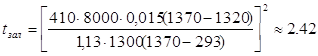 с
с
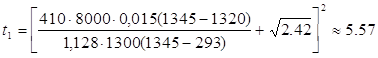 с
с
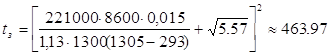 c
c
Скорость затвердевания во времени характеризуется следующим выражением:
![]() , где uЕ=(ТЕ-Тф)
, где uЕ=(ТЕ-Тф)
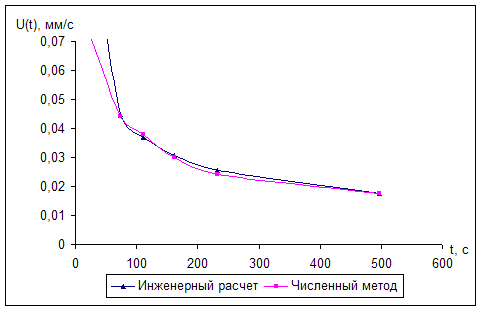
Результаты расчета
К= 1 DTA= 0 VS= 0 мм/с XF= 0 мм
К= 2 DTA= 5.293057 VS= 2.862526E-02 мм/с XF= .1515152 мм
К= 3 DTA= 2.12601 VS= 7.126739E-02 мм/с XF= .3030303 мм
К= 4 DTA= 1.877406 VS= 8.070453E-02 мм/с XF= .4545455 мм
К= 5 DTA= 1.782276 VS= 8.501218E-02 мм/с XF= .6060606 мм
К= 6 DTA= 1.751907 VS= 8.648586E-02 мм/с XF= .7575758 мм
К= 7 DTA= 1.744036 VS= 8.687617E-02 мм/с XF= .9090909 мм
К= 8 DTA= 1.781516 VS= 8.504844E-02 мм/с XF= 1.060606 мм
К= 9 DTA= 1.785084 VS= 8.487842E-02 мм/с XF= 1.212121 мм
К= 10 DTA= 1.842864 VS= 8.221721E-02 мм/с XF= 1.363636 мм
К= 11 DTA= 1.90608 VS= 7.949042E-02 мм/с XF= 1.515152 мм
К= 12 DTA= 1.943668 VS= 7.795321E-02 мм/с XF= 1.666667 мм
К= 13 DTA= 1.992883 VS= .0760281 мм/с XF= 1.818182 мм
К= 14 DTA= 2.077702 VS= 7.292438E-02 мм/с XF= 1.969697 мм
К= 15 DTA= 2.122164 VS= 7.139654E-02 мм/с XF= 2.121212 мм
К= 16 DTA= 2.2275 VS= 6.802025E-02 мм/с XF= 2.272727 мм
К= 17 DTA= 2.298877 VS= 6.590833E-02 мм/с XF= 2.424242 мм
К= 18 DTA= 2.341448 VS= 6.471001E-02 мм/с XF= 2.575758 мм
К= 19 DTA= 2.423752 VS= 6.251264E-02 мм/с XF= 2.727273 мм
К= 20 DTA= 2.485048 VS= 6.097072E-02 мм/с XF= 2.878788 мм
К= 21 DTA= 2.587401 VS= 5.855883E-02 мм/с XF= 3.030303 мм
К= 22 DTA= 2.708696 VS= 5.593657E-02 мм/с XF= 3.181818 мм
К= 23 DTA= 2.666805 VS= 5.681523E-02 мм/с XF= 3.333333 мм
К= 24 DTA= 2.704505 VS= 5.602324E-02 мм/с XF= 3.484848 мм
К= 25 DTA= 2.863065 VS= 5.292061E-02 мм/с XF= 3.636364 мм
К= 26 DTA= 2.975841 VS= 5.091507E-02 мм/с XF= 3.787879 мм
К= 27 DTA= 3.114344 VS= 4.865074E-02 мм/с XF= 3.939394 мм
К= 28 DTA= 3.144243 VS= 4.818812E-02 мм/с XF= 4.090909 мм
К= 29 DTA= 3.190864 VS= 4.748405E-02 мм/с XF= 4.242424 мм
К= 30 DTA= 3.175513 VS= .0477136 мм/с XF= 4.393939 мм
К= 31 DTA= 3.389869 VS= 4.469646E-02 мм/с XF= 4.545455 мм
К= 32 DTA= 3.432597 VS= 4.414009E-02 мм/с XF= 4.69697 мм
К= 33 DTA= 3.494103 VS= .0433631 мм/с XF= 4.848485 мм
К= 34 DTA= 3.509593 VS= 4.317171E-02 мм/с XF= 5 мм
К= 35 DTA= 3.836676 VS= 3.949126E-02 мм/с XF= 5.151515 мм
К= 36 DTA= 3.635523 VS= 4.167631E-02 мм/с XF= 5.30303 мм
К= 37 DTA= 3.73634 VS= 4.055175E-02 мм/с XF= 5.454545 мм
К= 38 DTA= 3.738327 VS= .0405302 мм/с XF= 5.606061 мм
К= 39 DTA= 3.985773 VS= 3.801399E-02 мм/с XF= 5.757576 мм
К= 40 DTA= 3.940797 VS= 3.844784E-02 мм/с XF= 5.909091 мм
К= 41 DTA= 3.992233 VS= 3.795248E-02 мм/с XF= 6.060606 мм
К= 42 DTA= 4.489356 VS= 3.374986E-02 мм/с XF= 6.212121 мм
К= 43 DTA= 4.140764 VS= 3.659111E-02 мм/с XF= 6.363636 мм
К= 44 DTA= 4.25704 VS= 3.559167E-02 мм/с XF= 6.515152 мм
К= 45 DTA= 4.390319 VS= 3.451119E-02 мм/с XF= 6.666667 мм
К= 46 DTA= 4.416203 VS= 3.430892E-02 мм/с XF= 6.818182 мм
К= 47 DTA= 4.198481 VS= 3.608809E-02 мм/с XF= 6.969697 мм
К= 48 DTA= 4.386362 VS= 3.454233E-02 мм/с XF= 7.121212 мм
К= 49 DTA= 4.594102 VS= 3.298036E-02 мм/с XF= 7.272727 мм
К= 50 DTA= 5.105144 VS= 2.967892E-02 мм/с XF= 7.424242 мм
К= 51 DTA= 4.779973 VS= 3.169791E-02 мм/с XF= 7.575758 мм
К= 52 DTA= 5.038644 VS= 3.007062E-02 мм/с XF= 7.727273 мм
К= 53 DTA= 5.035177 VS= 3.009133E-02 мм/с XF= 7.878788 мм
К= 54 DTA= 4.718354 VS= 3.211187E-02 мм/с XF= 8.030303 мм
К= 55 DTA= 5.019757 VS= 3.018376E-02 мм/с XF= 8.181818 мм
К= 56 DTA= 4.759093 VS= 3.183698E-02 мм/с XF= 8.333333 мм
К= 57 DTA= 5.686769 VS= 2.664345E-02 мм/с XF= 8.484849 мм
К= 58 DTA= 5.281692 VS= 2.868686E-02 мм/с XF= 8.636364 мм
К= 59 DTA= 5.195514 VS= 2.916269E-02 мм/с XF= 8.787879 мм
К= 60 DTA= 5.730412 VS= 2.644053E-02 мм/с XF= 8.939394 мм
К= 61 DTA= 5.444514 VS= 2.782896E-02 мм/с XF= 9.090909 мм
К= 62 DTA= 6.055304 VS= 2.502189E-02 мм/с XF= 9.242424 мм
К= 63 DTA= 5.745428 VS= 2.637143E-02 мм/с XF= 9.393939 мм
К= 64 DTA= 6.167727 VS= .0245658 мм/с XF= 9.545455 мм
К= 65 DTA= 6.239411 VS= 2.428357E-02 мм/с XF= 9.69697 мм
К= 66 DTA= 6.51199 VS= 2.326711E-02 мм/с XF= 9.848485 мм
К= 67 DTA= 6.397292 VS= 2.368427E-02 мм/с XF= 10 мм
К= 68 DTA= 6.57639 VS= 2.303926E-02 мм/с XF= 10.15152 мм
К= 69 DTA= 6.007806 VS= 2.521971E-02 мм/с XF= 10.30303 мм
К= 70 DTA= 5.742147 VS= .0263865 мм/с XF= 10.45455 мм
К= 71 DTA= 6.647415 VS= 2.279309E-02 мм/с XF= 10.60606 мм
К= 72 DTA= 7.110333 VS= 2.130915E-02 мм/с XF= 10.75758 мм
К= 73 DTA= 7.32001 VS= 2.069876E-02 мм/с XF= 10.90909 мм
К= 74 DTA= 7.206269 VS= 2.102547E-02 мм/с XF= 11.06061 мм
К= 75 DTA= 6.652145 VS= 2.277688E-02 мм/с XF= 11.21212 мм
К= 76 DTA= 6.866203 VS= .0220668 мм/с XF= 11.36364 мм
К= 77 DTA= 6.80113 VS= 2.227794E-02 мм/с XF= 11.51515 мм
К= 78 DTA= 6.100481 VS= 2.483659E-02 мм/с XF= 11.66667 мм
К= 79 DTA= 6.114481 VS= 2.477972E-02 мм/с XF= 11.81818 мм
К= 80 DTA= 6.5455 VS= 2.314799E-02 мм/с XF= 11.9697 мм
К= 81 DTA= 7.995783 VS= 1.894938E-02 мм/с XF= 12.12121 мм
К= 82 DTA= 6.699785 VS= 2.261493E-02 мм/с XF= 12.27273 мм
К= 83 DTA= 8.772509 VS= 1.727159E-02 мм/с XF= 12.42424 мм
К= 84 DTA= 6.788969 VS= 2.231785E-02 мм/с XF= 12.57576 мм
К= 85 DTA= 8.536396 VS= 1.774931E-02 мм/с XF= 12.72727 мм
К= 86 DTA= 8.794793 VS= 1.722782E-02 мм/с XF= 12.87879 мм
К= 87 DTA= 8.84897 VS= 1.712235E-02 мм/с XF= 13.0303 мм
К= 88 DTA= 7.511879 VS= 2.017007E-02 мм/с XF= 13.18182 мм
К= 89 DTA= 9.843055 VS= .0153931 мм/с XF= 13.33333 мм
К= 90 DTA= 9.162516 VS= 1.653641E-02 мм/с XF= 13.48485 мм
К= 91 DTA= 7.599952 VS= 1.993633E-02 мм/с XF= 13.63636 мм
К= 92 DTA= 6.998695 VS= 2.164906E-02 мм/с XF= 13.78788 мм
К= 93 DTA= 8.27722 VS= 1.830508E-02 мм/с XF= 13.93939 мм
К= 94 DTA= 9.549227 VS= 1.586675E-02 мм/с XF= 14.09091 мм
К= 95 DTA= 7.63567 VS= 1.984307E-02 мм/с XF= 14.24242 мм
К= 96 DTA= 9.736031 VS= 1.556231E-02 мм/с XF= 14.39394 мм
К= 97 DTA= 7.966977 VS= .0190179 мм/с XF= 14.54545 мм
К= 98 DTA= 7.350914 VS= 2.061174E-02 мм/с XF= 14.69697 мм
К= 99 DTA= 9.471897 VS= 1.599628E-02 мм/с XF= 14.84848 мм
К= 100 DTA= 8.533805 VS= .0177547 мм/с XF= 15 мм
Полное время затв. отл. TA= 497.1866 с.
Ср. скорость охл. на оси отл. Voxl= 6.536781E-02 K/с
Ср. скорость затв. отл. Vz= 3.016976E-02 мм/с
K=1
T( 10 )= 1345 Vox= 0
T( 20 )= 1345 Vox= 0
T( 30 )= 1345 Vox= 0
T( 40 )= 1345 Vox= 0
T( 50 )= 1345 Vox= 0
T( 60 )= 1345 Vox= 0
T( 70 )= 1345 Vox= 0
T( 80 )= 1345 Vox= 0
T( 90 )= 1345 Vox= 0
T( 100 )= 1345 Vox= 0
K= 10
T( 10 )= 1312.5 K Vox= 1.132695E-02 K/c
T( 20 )= 1312.652 K Vox= 4.159837E-02 K/c
T( 30 )= 1312.797 K Vox= 7.286339E-02 K/c
T( 40 )= 1312.933 K Vox= .1022737 K/c
T( 50 )= 1313.054 K Vox= .1295644 K/c
T( 60 )= 1313.159 K Vox= .1536093 K/c
T( 70 )= 1313.242 K Vox= .1736798 K/c
T( 80 )= 1313.303 K Vox= .1881863 K/c
T( 90 )= 1313.341 K Vox= .1965987 K/c
T( 100 )= 1313.354 K Vox= .1992483 K/c
K= 20
T( 10 )= 1311.603 K Vox= 2.421711E-02 K/c
T( 20 )= 1312.5 K Vox= 6.38585E-04 K/c
T( 30 )= 1312.495 K Vox= 7.859508E-03 K/c
T( 40 )= 1312.492 K Vox= 1.291907E-02 K/c
T( 50 )= 1312.489 K Vox= 1.630848E-02 K/c
T( 60 )= 1312.487 K Vox= 1.817511E-02 K/c
T( 70 )= 1312.485 K Vox= 1.945228E-02 K/c
T( 80 )= 1312.484 K Vox= 1.979613E-02 K/c
T( 90 )= 1312.483 K Vox= 1.925579E-02 K/c
T( 100 )= 1312.483 K Vox= 1.886282E-02 K/c
K= 30
T( 10 )= 1311.093 K Vox= 2.279559E-02 K/c
T( 20 )= 1311.792 K Vox= 2.387194E-02 K/c
T( 30 )= 1312.5 K Vox= 1.153234E-04 K/c
T( 40 )= 1312.513 K Vox=-2.806202E-03 K/c
T( 50 )= 1312.521 K Vox=-4.612935E-03 K/c
T( 60 )= 1312.528 K Vox=-5.996816E-03 K/c
T( 70 )= 1312.531 K Vox=-6.842521E-03 K/c
T( 80 )= 1312.534 K Vox=-7.342256E-03 K/c
T( 90 )= 1312.536 K Vox=-7.611343E-03 K/c
T( 100 )= 1312.537 K Vox=-7.726667E-03 K/c
K= 40
T( 10 )= 1310.788 K Vox= 2.487376E-02 K/c
T( 20 )= 1311.353 K Vox= 2.419229E-02 K/c
T( 30 )= 1311.923 K Vox= 2.053712E-02 K/c
T( 40 )= 1312.5 K Vox=-6.504969E-04 K/c
T( 50 )= 1312.517 K Vox=-1.050088E-02 K/c
T( 60 )= 1312.529 K Vox=-.0177183 K/c
T( 70 )= 1312.538 K Vox=-2.298423E-02 K/c
T( 80 )= 1312.543 K Vox=-2.679428E-02 K/c
T( 90 )= 1312.547 K Vox=-2.921041E-02 K/c
T( 100 )= 1312.548 K Vox=-3.004676E-02 K/c
K= 50
T( 10 )= 1310.654 K Vox=-1.673787E-02 K/c
T( 20 )= 1311.12 K Vox=-.0125534 K/c
T( 30 )= 1311.584 K Vox=-6.719058E-03 K/c
T( 40 )= 1312.044 K Vox= 6.456035E-04 K/c
T( 50 )= 1312.5 K Vox= 6.934259E-04 K/c
T( 60 )= 1312.529 K Vox= 9.325384E-04 K/c
T( 70 )= 1312.552 K Vox= 1.315118E-03 K/c
T( 80 )= 1312.568 K Vox= 1.769432E-03 K/c
T( 90 )= 1312.577 K Vox= 2.152011E-03 K/c
T( 100 )= 1312.58 K Vox= 2.295479E-03 K/c
K= 60
T( 10 )= 1310.483 K Vox=-7.690089E-03 K/c
T( 20 )= 1310.888 K Vox=-5.794195E-03 K/c
T( 30 )= 1311.294 K Vox=-3.621372E-03 K/c
T( 40 )= 1311.698 K Vox=-7.455765E-04 K/c
T( 50 )= 1312.1 K Vox= 3.067515E-03 K/c
T( 60 )= 1312.5 K Vox=-1.917197E-04 K/c
T( 70 )= 1312.512 K Vox=-4.111322E-03 K/c
T( 80 )= 1312.52 K Vox=-6.752793E-03 K/c
T( 90 )= 1312.524 K Vox=-8.329155E-03 K/c
T( 100 )= 1312.526 K Vox=-8.819105E-03 K/c
K= 70
T( 10 )= 1310.231 K Vox= 1.985558E-02 K/c
T( 20 )= 1310.595 K Vox= .0195367 K/c
T( 30 )= 1310.965 K Vox= 1.845251E-02 K/c
T( 40 )= 1311.339 K Vox= 1.677308E-02 K/c
T( 50 )= 1311.72 K Vox= .0142433 K/c
T( 60 )= 1312.106 K Vox= 1.096946E-02 K/c
T( 70 )= 1312.5 K Vox=-1.700692E-04 K/c
T( 80 )= 1312.511 K Vox=-3.571454E-03 K/c
T( 90 )= 1312.517 K Vox=-5.591026E-03 K/c
T( 100 )= 1312.52 K Vox=-6.483889E-03 K/c
K= 80
T( 10 )= 1310.199 K Vox=-1.605722E-02 K/c
T( 20 )= 1310.521 K Vox=-1.469581E-02 K/c
T( 30 )= 1310.844 K Vox=-1.286816E-02 K/c
T( 40 )= 1311.171 K Vox=-1.066751E-02 K/c
T( 50 )= 1311.499 K Vox=-7.664945E-03 K/c
T( 60 )= 1311.829 K Vox=-3.74855E-03 K/c
T( 70 )= 1312.163 K Vox= 7.08681E-04 K/c
T( 80 )= 1312.5 K Vox= 1.86495E-04 K/c
T( 90 )= 1312.496 K Vox= 2.275239E-03 K/c
T( 100 )= 1312.495 K Vox= 3.058518E-03 K/c
K= 90
T( 10 )= 1310.395 K Vox= 9.206051E-03 K/c
T( 20 )= 1310.673 K Vox= 9.379247E-03 K/c
T( 30 )= 1310.946 K Vox= 9.39257E-03 K/c
T( 40 )= 1311.216 K Vox= 9.072823E-03 K/c
T( 50 )= 1311.48 K Vox= 8.593203E-03 K/c
T( 60 )= 1311.741 K Vox= 7.727221E-03 K/c
T( 70 )= 1311.999 K Vox= 6.328328E-03 K/c
T( 80 )= 1312.251 K Vox= 4.649655E-03 K/c
T( 90 )= 1312.5 K Vox=-5.329118E-05 K/c
T( 100 )= 1312.503 K Vox=-6.528169E-04 K/c
K= 100
T( 10 )= 1310.187 K Vox= 9.684027E-03 K/c
T( 20 )= 1310.446 K Vox= 9.884289E-03 K/c
T( 30 )= 1310.703 K Vox= 1.009885E-02 K/c
T( 40 )= 1310.96 K Vox= 9.869983E-03 K/c
T( 50 )= 1311.217 K Vox= 9.211984E-03 K/c
T( 60 )= 1311.474 K Vox= 8.425247E-03 K/c
T( 70 )= 1311.731 K Vox= 7.495466E-03 K/c
T( 80 )= 1311.988 K Vox= 6.293903E-03 K/c
T( 90 )= 1312.244 K Vox= 4.734731E-03 K/c
T( 100 )= 1312.5 K Vox= 1.430432E-05 K/c