
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология и педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по информатике программированию
Краткое содержание произведений
Реферат: Практические задачи по ТОУЭС
Реферат: Практические задачи по ТОУЭС
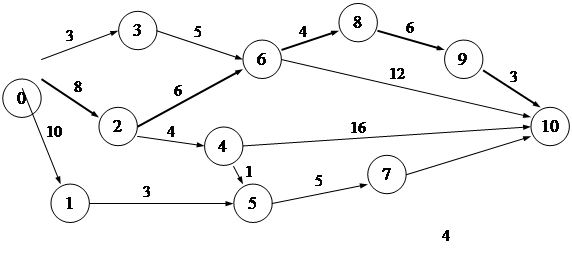
1. Рассчитайте параметры сетевого графа
|
Работа i, j |
Продол. |
Ранние сроки | Поздние сроки |
Полный
резерв |
Свободн.
резерв |
||
|
tiPH |
tjPO |
tiПH |
tjПО |
||||
| (0, 1) | 10 | 0 | 10 | 5 | 15 | 5 | 5 |
|
(0, 2) |
8 | 0 | 8 | 0 | 8 |
0К |
0 |
| (0, 3) | 3 | 0 | 3 | 6 | 9 | 0 | 0 |
| (1, 5) | 3 | 10 | 13 | 15 | 18 | 5 | 5 |
| (2, 4) | 4 | 8 | 12 | 9 | 13 | 1 | 1 |
|
(2, 6) |
6 | 8 | 14 | 8 | 14 |
0К |
0 |
| (3, 6) | 5 | 3 | 8 | 9 | 14 | 6 | 6 |
| (4, 5) | 1 | 12 | 13 | 17 | 18 | 5 | 5 |
| (4, 10) | 16 | 12 | 28 | 11 | 27 | -1 | -1 |
| (5, 7) | 5 | 13 | 18 | 18 | 23 | 5 | 5 |
|
(6, 8) |
4 | 14 | 18 | 14 | 18 |
0К |
0 |
| (6, 10) | 12 | 14 | 26 | 15 | 27 | 1 | 1 |
| (7, 10) | 4 | 18 | 22 | 23 | 27 | 5 | 5 |
|
(8, 9) |
6 | 18 | 24 | 18 | 24 |
0К |
0 |
|
(9, 10) |
3 | 24 | 27 | 24 | 27 |
0К |
0 |
К – критические операции
Продолжительность критического пути: 8 + 6 + 4 + 6 + 3 = 27
2. Оценить с
достоверностью 90% оптимистичный
и пессимистичный срок завершения работ.
|
Эксперты |
|||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 6 | 7 | 6 | 5 | 4 | 4 | 4 | 5 | 6 | 6 | 6 | 4 | 4 | 8 | 10 | 3 | 4 | 4 | 5 | 6 |
Упорядочиваем по возрастанию:
10, 8, 7, 6, 6, 6, 6, 6, 6, 5, 5, 5, 4, 4, 4, 4, 4, 4, 4, 3
Отбрасываем первые два значения и находим Qопт:
Qопт = 89 / 18 = 4,94
Упорядочиваем по убыванию и аналогично находим Qпес:
Qпес = 100 / 18 = 5,55
Находим Qср:
Qср = 107 / 20 = 5,35
Отклонение Qопт от Qср – 7,6%; Qпес от Qср – 3,7%. Оба значения в пределах 10%, таким образом достоверность 90% обеспечена.
3. Рассчитать
требуемое количество экспертов, при котором влияние
1 эксперта на среднюю оценку составляет не более x = 9%.
Пробная оценка x + 1 экспертов:
6, 7, 6, 5, 4, 4, 4, 5, 6, 6
х = 9% => 0,91 £ E £ 1,09
Qср = 53 / 10 = 5,3
b = 10
T = ![]()
Таким образом, 9 человек – требуемое количество экспертов для проведения групповой оценки с влиянием одного эксперта не более 9%.
4. Проверить оптимальность указанных планов
f (x) = 3 x1 + 2 x2 – 4 x3 +5 x4 –> max
3 x1 + 2 x2 + 2 x3 – 2 x4 ³ -1
2 x1 + 2 x2 + 3 x3 – x4 ³ -1
x1 ³ 0 x2 ³ 0
x3 ³ 0 x4 ³ 0
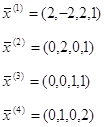
Координаты вектора x(1) не соответствуют ограничениям, т .к. х2 < 0
Остальные векторы подставляем в систему неравенств:
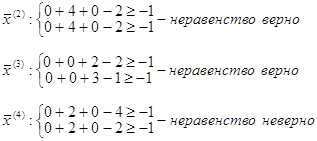
Таким образом, вектор х (4) тоже не удовлетворяет условиям. Вычисляем значения f(x):
x(2): f (x) = 0 + 4 – 0 + 5 = 9
x(3): f (x) = 0 + 0 - 4 + 5 = 1
Функция достигает максимума в x(2) (0, 2, 0, 1).
5. Решить графически задачу линейного программирования:
f (x) = 2 x1 + 4 x2 –> min
x1 + 2 x2 £ 5
3 x1 + x2 ³ 5
0 £ x1 £ 4 0 £ x2 £ 4
Найдем множество решений неравенств:
х1 + 2 х2 £ 5, если х1 = 0, то х2 £ 2,5
если х2 = 0, то х1 £ 5 точки прямой 1: (0; 2,5) и (5; 0)
3 х1 + х2 ³ 5, если х1 = 0, то х2 ³ 5
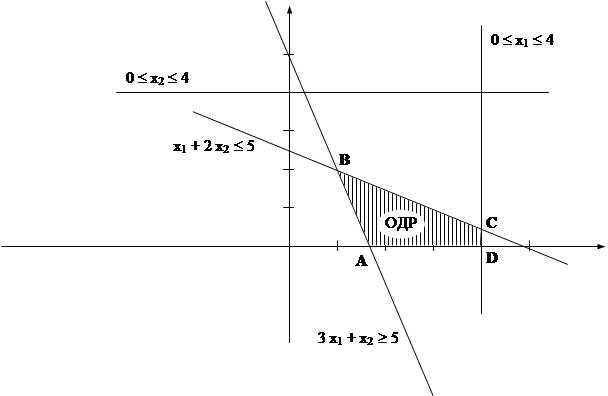 если
х2 = 0, то х1 ³ 1, 67 точки прямой 2:
(0; 5) и (1,67; 0)
если
х2 = 0, то х1 ³ 1, 67 точки прямой 2:
(0; 5) и (1,67; 0)
Найдем координаты точек A, B, C, D:
A (1,67; 0) и D (4; 0) – из неравенств
B (1; 2)
как точка пересечения прямых из системы ![]()
С (4; 0,5) – x1 = 4 из неравенства x1<4, а x2 из уравнения 4 + 2 x2 = 5
Вычислим значение функции в этих точках:
A: f (x) = 2 * 1,67 + 4 * 0 = 3,33
B: f (x) = 2 * 1 + 4 * 2 = 10
C: f (x) = 2 * 4 + 4 * 0,5 = 10
D: f (x) =2 * 4 + 4 * 0 = 8
Функция принимает минимальное значение в точке A (1,67; 0).
6. Решить задачу
Механический завод при изготовлении 3-х разных деталей использует токарный, фрезерный и строгальный станки. при этом обработку каждой детали можно вести 2-мя разными способами. В таблице указаны ресурсы времени каждой группы станков, нормы времени при обработке детали на соответствующем станке по данному технологическому способу и прибыль от выпуска единицы детали каждого вида.
|
Норма времени, станко/час |
Ресурсы времени |
||||||
|
Станок |
I деталь |
II деталь |
III деталь |
||||
|
1 |
2 |
1 |
2 |
1 |
2 |
||
|
Токарный |
0,4 | 0,9 | 0,5 | 0,5 | 0,7 | – | 250 |
|
Фрезерный |
0,5 | – | 0,6 | 0,2 | 0,3 | 1,4 | 450 |
|
Строгальный |
0,3 | 0,5 | 0,4 | 1,5 | – | 1,0 | 600 |
|
Прибыль |
12 | 18 | 30 | ||||
Определить производственную программу, обеспечивающую максимальную прибыль.
Решение:
Пусть x1, x2, x3 – загрузка станков.
Таким образом 0 £ x1 £ 250;
0 £ x2 £ 450;
0 £ x3 £ 600.
При первом способе технологической обработки получаем:
0,4 x1 + 0,5 x2 + 0,7 x3 £ 250
0,5 x1 + 0,6 x2 + 0,3 x3 £ 450
0,3 x1 + 0,4 x2 £ 600
0,4 x1 + 0,5 x2 + 0,3 x3 ³ 12
0,5 x1 + 0,6 x2 + 0,4 x3 ³ 18
0,7 x1 + 0,3 x2 ³ 30
Необходимо найти решение, при котором f (x) = 12 x1 + 18 x2 + 30 x3 –> max
Каноническая форма записи:
x1 > 0, x2 > 0, x3 > 0, xi > 0, i = 4, 5,…12
x1 + x4 = 250; x2 + x5 = 450; x3 + x6 = 600
0,4 x1 + 0,5 x2 + 0,7 x3 + x7 = 250
0,5 x1 + 0,6 x2 + 0,3 x3 + x8 = 450
0,3 x1 + 0,4 x2 + x9 = 600
0,4 x1 + 0,5 x2 + 0,3 x3 – x10 = 12
0,5 x1 + 0,6 x2 + 0,4 x3 – x11 = 18
0,7 x1 + 0,3 x2 + x12 = 30
f (x) = 12 x1 + 18 x2 + 30 x3 –> max
Стандартная форма записи:
x1 > 0, x2 > 0, x3 > 0
x1 £ 250, x2 £ 450, x3 £ 600
-0,4 x1 - 0,5 x2 - 0,7 x3 ³ -250
-0,5 x1 - 0,6 x2 - 0,3 x3 ³ -450
-0,3 x1 - 0,4 x2 ³ -600
-0,4 x1 - 0,5 x2 - 0,3 x3 £ -12
-0,5 x1 - 0,6 x2 - 0,4 x3 £ -18
-0,7 x1 - 0,3 x2 £ -30
f (x) = -12 x1 - 18 x2 - 30 x3 –> min
Находим, что: x1 = 0,25 x2 = 0,8 x3 = 277
Значение функции: f (x) = 12 * 0,25 + 18 * 0,8 + 30 * 277 = 10082