Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология и педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по информатике программированию
Краткое содержание произведений
Реферат: О возможности универсального кода внутреннего представления программы
Реферат: О возможности универсального кода внутреннего представления программы
Михаил Козлов
Введение
Статья Андерсона [1], которому, видимо, принадлежит сама идея схемной реализации языка программирования высокого уровня, появилась практически одновременно (1961г.) если не с зарождением этих языков (FORTRAN, 1949), то с выходом их «на широкую арену» (COBOL, 1959, ALGOL-60 как попытка «официального языка публикаций алгоритмов» и т.п.). В действительности же предыстория проблемы охватывает бóльшие временные интервалы, а сама проблема глубже, чем это может представиться на первый взгляд. Неслучайно строгое формулирование понятия алгоритма непосредственно предшествовало появлению первых вычислительных машин. Очевидно, что этот факт есть следствие тесной связи алгоритма с тем «субъектом», который этот алгоритм реализует. Поэтому первым строгим определением алгоритма явилось именно понятие машины (автомата) Тьюринга (1936г.). В отличие от этой чисто математической абстракции в основе подавляющего большинства когда-либо созданных до сих пор компьютеров лежит более богатая деталями схема, являющаяся всё же в том или ином смысле эквивалентным автомату Тьюринга определением алгоритма – фон Неймановская архитектура вычислительной машины (1945г.), с которой непосредственно связано представление вычислительных алгоритмов командными программами.
Вывод, который можно извлечь из сказанного, состоит в некой нетривиальности взаимоотношения между «хардом» и «софтом». При этом использование алгоритмического языка высокого уровня можно рассматривать как моделирование более сложной машины средствами простой, что соответствует обычному понятию о «языковом процессоре». Ясно, что такая многоступенчатость делает компьютер более загадочным и недоступным, чем он представлялся изначально, и чем он является на самом деле. Среди практических попыток все же «образумить» и «очеловечить хард» можно выделить получившие некоторое распространение ЭВМ серии «Мир» (СССР) [2, 3] со схемной реализацией алголоподобного входного языка и «Систему 432» фирмы Intel [4], являющуюся, по-видимому, последним по времени (80-е годы) экспериментом в этом направлении. Однако в целом, как очевидно, эти попытки не оказались продуктивными.
Наиболее существенные ограничения здесь состоят в значительном усложнении устройства языковой машины на всех уровнях ее функциональной схемы и заметном снижении ее быстродействия в сравнении с командным компьютером. При этом также утрачивается или значительно ослабевает одно из фундаментальных свойств компьютера – его универсальность. Хотя на языковой машине в принципе можно реализовать любой из существующих алгоритмических языков, своеобразная несовместимость многих из них может порождать значительную неэффективность работы программы, написанной на «чужом» языке. При этом также общая математическая «неудобность» алгоритма как абстрактного объекта вообще и достаточно обычная сложность алгоритмических проблем в частности уже давно привели к отказу от мысли об «универсальном» языке программирования либо ином подобном инструментальном средстве, которое могло бы быть одинаково пригодным и эффективным в решении любых задач, на схемную реализацию которого было бы не жалко тратить усилия.
Тем не менее, в течение всего периода существования электронной вычислительной техники протекает процесс накопления практического опыта, одним из аспектов которого служит продолжающаяся отработка и самого понятия алгоритма и естественное развитие изначально искусственно созданного «языка компьютера» в его многообразных «диалектах». Здесь можно выделить как один из ярких ранних (1968г.) примеров принцип программирования без оператора перехода (go to) [5], эффективность которого объяснить и обосновать было достаточно затруднительно.
В начальных этапах развития вычислительной техники ситуация, когда набор командных кодов процессора менялся параллельно с разработкой его математического обеспечения была нередкой. Коды вводились и вычищались из системы команд в соответствие с мнением программиста об их необходимости или ненужности. Массовое распространение компьютеров и стандартизация «софта» сделало животрепещущей проблему совместимости кодовых таблиц и переносимости матобеспечения, и оснащение очередного Pentium'а дополнительным набором графических команд реализуется как длительно подготавливаемая акция, «рыночная» ответственность которой несопоставима с почти хулиганским по сегодняшним меркам отношением к кодовым наборам полууникальных ЭВМ 60-х годов.
То, что мы хотим предложить в настоящей статье, можно рассматривать в аналогии с упомянутым графическим расширением, в отношении, однако, к «языковой» проблеме. При этом соответствующее действие нельзя свести к простому расширению системы команд, так как оно влечет перестройку и реорганизацию основной функциональной схемы самого исполняющего ядра вычислительной системы, хотя и сохраняющего значительную долю преемственности по отношению к современной. А именно, предлагается переход на операторно-формульный код как некую версию расширения командного представления программы, с единственной существенной особенностью: допущением формульного представления аргументов оператора (команды или инструкции) программы.
Следующие обстоятельства позволяют полагать, что данный подход может представить реальный практический интерес.
Используемое в качестве внутреннего кода представление программы последовательностью операторов со списками аргументов с одной стороны, универсально близко практически любому алгоритмическому языку, с другой – при всей своей «языковости» сохраняет наибольшее подобие командной программе с присущей или приписываемой ей особой гибкостью.
Исполняющее устройство для формульной программы по уровню сложности и быстродействию соответствует обычному командному процессору, в отличие от известных систем схемной реализации языка высокого уровня.
Трансляция любого входного языка в формульный код существенно проще трансляции в командный код, при этом также значительно упрощается любой контроль выполняемой программы (например, при ее отладке).
Соответствующее символьное представление алгоритма почти не содержит специфических элементов и весьма близко к распространенной общематематической символике. Операторно-формульный код, таким образом, имеет некую «объективную» основу, снижающую разнообразие возможных его вариантов, в противовес системам команд обычных процессоров, многообразие которых может быть приведено к некоторому единству лишь более или менее принудительной либо вынужденной стандартизацией.
Формульное ядро позволяет наиболее естественным образом дооснащать схему дополнительными средствами аппаратной поддержки языковых и иных информационно-логических структур.
Алгоритмические формулы
Основным видом элементов практически любого языка высокого уровня являются оператор или функция в следующей записи:
имя оператора или функции (аргумент1,..., аргументn).
Инструкция (команда) машинного языка чаще всего выглядит примерно так:
код команды | операнд1 | операнд2.
Как видим, в наиболее обобщенной форме эти конструкции достаточно сходны. Наибольшее отличие состоит в том, что аргументы оператора могут представлять собой формульные выражения, включающие в себя множество переменных, знаков операций, скобок и идентификаторов функций, в то время как операнды команды могут быть лишь индивидуальными адресными ссылками на ячейки оперативной памяти. Но именно наличие формул в языке составляет самую «неприятную», если не сложную для обработки составляющую часть символьной программы, так как при их трансляции нарушается естественное линейное соответствие между командами объектной программы и лингвистическими конструкциями исходной записи алгоритма.
Теперь мы можем представить, что элементами формулы являются те же адресные ссылки на ячейки памяти, соответствующие переменным, коды операций, скобок и иных символьных ограничителей, а также ссылки на подпрограммы-функции, аналогичные тем, которые используются в командах прерывания на подпрограмму. Таким образом, в роли отдельного элемента (псевдокоманды) такой «формульной» программы выступит практически тот же символ (переменная, код (имя) оператора, код операции, символ-ограничитель, код (имя) подпрограммы-функции и т.д.), что и в языке высокого уровня. При этом однако, эти элементы функционально должны быть связаны более тесно, чем команды обычной программы, и наименьшей замкнутой выполняемой (так сказать, «с результатом») единицей явится все же целостный оператор, сложность строения которого в принципе ограничена лишь ресурсом оперативной памяти.
Как известно [6], «наименьший» универсальный язык может быть сведен к простым переменным, операторам присваивания и операторам условного и безусловного перехода. Этот набор соответствует языку логических схем Ляпунова – Янова (ЯЛС) [7...9], являющемуся одной из ранних математических моделей языка программирования высокого уровня. Отметим, что первые из получивших наибольшее распространение языков высокого уровня (FORTRAN, COBOL, ALGOL...) были далеко не минимальны по составу своих изобразительных средств и при этом значительно отличались друг от друга. Однако с течением времени сформировалось достаточно определенное ядро из набора операторов, систематически воспроизводящихся в большинстве современных языков.
Таблица 1
Соответствие операторно-формульного представления алгоритма операторам языка BASIC
| Символ и его название | Операторы BASIC | |
| (f) | загрузка контекста | SELECT CASE f |
| (x, f) | присваивание (загрузка) | x = f |
| (x, f, ..., g) | циклическая загрузка | – |
| └(M) | отсылающая полускобка Янова | GOTO M |
| └(t, M) | условная полускобка Янова | IF t THEN GOTO M |
| ┘(M) | принимающая полускобка Янова | M: |
| [(t) | открывающая условная скобка | IF t THEN |
| ][ | else-скобка | ELSE |
| ] | закрывающая условная скобка | END IF |
| { | открывающая цикловая скобка | DO |
| {(t) | открывающая цикловая скобка | <DO> WHILE t |
| {(n) | открывающая цикловая скобка | FOR loop = 1 TO n |
| {(M, k) | открывающая цикловая скобка | FOR loop = M TO k |
| {(M, k, l) | открывающая цикловая скобка | FOR loop = M TO k STEP l |
| } | закрывающая цикловая скобка | NEXT или LOOP |
| }(t) | закрывающая цикловая скобка | <LOOP> WHILE t |
| C[ | контекстная открывающая условная скобка (при логическом, арифметическом или строковом контексте) | CASE –1, |
| CASE IS<>0 или | ||
| CASE IS<>"" | ||
| C[(g) | контекстная открывающая у.с. | CASE g |
| E[ | контекстная else-скобка | CASE ELSE |
Здесь t – логическое выражение; n – целое неотрицательное выражение; m, k, l – арифметические (т.е. целые либо вещественные) выражения; s – строковое; f, g – произвольные выражения; x – переменная, M – метка.
Алгоритмические формулы (АФ; табл.1, рис.1) представляют собой формальную систему, являющуюся развитием ЯЛС посредством включения в него конструкций, адекватных упомянутому языковому ядру. Главным фактом, лежащим в основе этого формализма, является возможность рассматривать основные элиминаторы оператора перехода – условные операторы, операторы выбора и операторы организации цикла, – как особые (операторные) скобки, в принципе аналогичные обычным по своим свойствам и функциям. В соответствии с этим «программа» рассматривается как скобочное выражение (строка), структура которого оформляется тремя видами скобок: алгебраическими (круглыми), условными (прямыми) и цикловыми (фигурными).

Рис. 1. Алгоритм Евклида нахождения наибольшего общего делителя в представлении различными языками программирования: I – на языке логических схем (Ляпунов, Янов, 1958), II – на одном из наиболее распространенных языков программирования (BASIC) в «старой» (A) и «новой» (B) нотации, III – в виде алгоритмической формулы, адекватной коду формульного процессора
Элементом алгоритмической формулы является оператор, состоящий из имени оператора и списка аргументов, заключенного в алгебраические скобки. Алгоритмическая формула (см. рис.1) является последовательностью операторов, отделяемых друг от друга знаком-разделителем (точка с запятой). Основу формализма составляют оператор сохранения значения (присваивание) и операторы-скобки, именами которых служат символы фигурных (цикловых) либо квадратных (операторы условий и выбора) скобок. Условные и цикловые скобки аналогичны соответствующим операторам большинства распространенных языков (табл.1 и рис.1). Например, открывающая прямая скобка в качестве имени оператора, с логическим условием в качестве единственного аргумента, и парный ей оператор закрывающей скобки, не имеющий аргументов, ограничивают подпоследовательность операторов, выполняющуюся, если выполнено данное логическое условие. Подобные парные операторы, именами которых являются символы скобок, ограничивают подстроку, выполняющуюся кратное число раз, заданное значением параметра цикла, либо в зависимости от выполнения соответствующего логического условия. Оператор присваивания является безымянным, традиционная запись x:=F(y1,..., yn) отвечает оператору (x, F(y1,..., yn)). Множество всех остальных («именованных») операторов, наборы функций и отношений, как и допустимые классы переменных или иные ограничительные символы, могут быть в той или иной степени специфичными.
Таким образом, алгоритмическая формула отличается от ЯЛС главным образом в том отношении, что, с одной стороны, наиболее последовательно проводится принцип линеаризации записи алгоритма с полностью унифицированным операторным представлением его элементов, с другой – в соответствии со сложившейся практикой в формализм введены наиболее распространённые средства элиминации операторов перехода (операторы-скобки).
В алгоритмических формулах легко усматривается естественное развитие обычной функционально-алгебраической символики. Уже при вычислении простейших выражений возникает необходимость сохранять промежуточные результаты. В обычных (алгебраических или арифметических) формулах этот процесс однозначен. Более общая ситуация требует явного введения ячеек-переменных. Подобным образом, операторы-скобки являются лишь обобщением алгебраических, определяющих последовательность действий с входящими в выражение объектами. В связи с этим мы считаем возможным рассматривать АФ как расширение общематематической семиотики, а не как язык программирования или его математическую модель. Поэтому мы полагаем также допустимыми любые возможные расширения (клоны) этого языка, сколь угодно своеобразные в зависимости от контекста различных сфер его применения. В частности, в соответствующих ситуациях, легко представить применение в составе АФ любой известной общематематической символики – кванторов, производных, интегралов, – и т.п., лишь бы при этом формула оставалась «понятной» в той же, например, степени, в какой понятно доказательство какого-либо математического утверждения, как правило не доводимое до уровня совершенной формально-логической строгости. В этом ракурсе и сам ЯЛС можно трактовать как частный случай или клон АФ.
Можно было бы отдельно рассмотреть вопрос о минимальности набора собственных символов АФ: в сущности достаточна лишь одна разновидность операторных скобок – цикловые, с блокировкой тела цикла при нулевом значении числа повторений. Даже логико-алгебраические формулы для АФ-термов в каком-то смысле являются расширением языка, можно было бы обойтись и чисто функциональной записью выражений. Однако очевидно, что в соответствие с общими тенденциями развития минимальность набора непосредственно выполняемых процессором операций ни в каком отношении не является целью, фактически в качестве таковой выступают достаточно трудно и медленно вырабатываемые иные критерии оптимальности этого набора. Представляемый подход состоит в том, что сущностью АФ объявляется общематематический смысл некоторых специфически программистских по происхождению символов – присваиваний и операторных скобок. Их использование может быть уподоблено практике применения формально-логических по происхождению знаков кванторов или функциональных символов интегрирования и дифференцирования. Конкретизация («локализация») соответствующего формализма в строго определенное исчисление или алгоритмический код так или иначе должна быть привязана к контексту ситуации и в общем виде не производится, как она не производится и для приведенных аналогичных объектов.
В алгебраической интерпретации [6, 10] нормальная (без полускобок Янова) алгоритмическая формула – это свободная конструкция над алгеброй функций внутренних состояний (ВС) некоего автоматического устройства (АУ) и тем или иным множеством именованных операторов, выделенное подмножество которых характеризуется как «действия» АУ, а остальные выступают в роли вызовов подпрограмм (т.е., в конечном счете, как сокращения). При этом, при «выполнении» АФ, из нее удаляются все внутренние переменные и операторы преобразования внутреннего состояния (элиминация ВС), а аргументы остающихся в результирующей строке именованных операторов-действий получают определяемое значение. Таким образом, АФ как формальный объект играет роль шаблона, по которому, при заданном векторе условий, по определенным правилам, вычисляется выходная строка действий АУ.
Синтаксическая правильность АФ складывается из правильности строения термов и операторов, соблюдения парности входящих в неё скобочных операторов и правильности чередования условных и цикловых скобок. Семантическая правильность весьма естественно определяется как элиминируемость ВС на элементах обусловленного подмножества допустимых вариантов входного файла. Семантически тождественные на данном множестве входных условий формулы порождают на нем идентичные последовательности действий, выбор подмножества действий среди операторов, таким образом, предопределяет это отношение.
Операторно-формульная запись алгоритма, в отличие от языкового или командного, наиболее удобна как для исследования, так и машинного анализа, генерации и оптимизации программного кода. Она также наиболее естественно («исчислительно») представляет объекты алгоритмической природы, подобные программам, что существенно, коль скоро речь идет о возможности формирования нового стандарта внутреннего представления программ. Более того, мы полагаем, что формульная запись, наряду с общепринятыми рекурсивными функциями, автоматом Тьюринга или алгорифмами Маркова, наиболее пригодна выступать в роли «программной» версии определения алгоритма вообще. Язык программирования как технический объект в АФ редуцируется практически полностью, сводясь лишь к нескольким символам и правилам общематематического характера, причем это не сопровождается введением каких-либо специфических объектов или знаков, таких, как метки передачи управления.
Формульный процессор
Главной характеристикой АФ, как мы считаем, является возможность построения для них исполняющего устройства – процессора с формульной архитектурой ([11], рис.2), – по уровню сложности и быстродействию сопоставимого с существующими командными процессорами. Это существенно отличает данный процессор от любой известной системы схемной реализации, для которых характерно многоуровневое усложнение логики исполняющей системы с включением в нее множества дополнительных регистров (иногда столь специфичных, как, например, счетчики скобок), связей, логических схем, прошитых в ПЗУ программных модулей, фактически интерпретирующих в конечном счете операторы входного языка и т.д. и т.п. В отличие от этого, базовая идея формульной архитектуры может быть отражена в одной фразе: для организации прямого выполнения операторно-формульного кода программы в код исполняемой команды включаются флаги декларируемого состояния загрузки ряда регистров местной (внутрипроцессорной) памяти. Такой упрощающий подход к исполнительной системе соответствует более адекватному распределению функций между ней и системами транслирующими либо интерпретирующими. Более сильная подгонка схемы под тот или иной язык или инструментальное средство на сегодняшний день выглядит нецелесообразной. В случае формульного процессора все программные средства остаются в равном положении по отношению к исполняющей системе, а транслирующая фаза хотя и заметно упрощается, всё же сохраняется как таковая, сохраняя вместе с собой и естественную возможность использования самых причудливых приёмов программирования и управляющих протоколов.
|
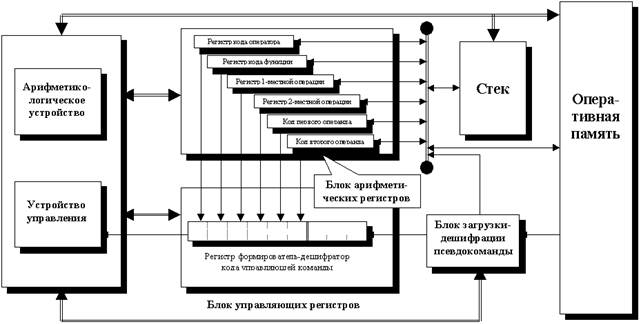
Рис. 2. Возможная функциональная схема формульного процессора Главной идеей, лежащей в основе формульного процессора является включение флагов состояния загрузки регистров местной (внутрипроцессорной) памяти в код выполняемой команды для организации прямого вычисления формульных выражений. Флаги загрузки составляют часть битов регистра формирователя-дешифратора кода команды управления. Другую его часть составляют признаки кода очередной псевдокоманды, представляющей тот или иной символ операторно-формульного кода.
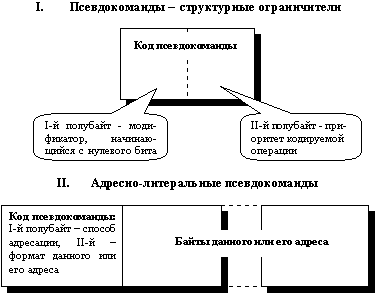
Рис. 3. Структура псевдокоманд формульного процессора Программа-эмулятор формульного процессора представляет собой информационно-логическую модель, реализующую пример системы кодов псевдокоманд и тактовой схемы процессора. Псевдокоманды – структурные ограничители являются однобайтными кодами символов-ограничителей алгоритмических формул (знаки арифметико-логических операций, скобки, знаки-разделители, коды выделенных операторов). Адресно-литеральные псевдокоманды состоят из однобайтного кода-определителя, описывающего формат и способ адресации данного, и самого этого данного либо соответствующей адресной ссылки. В адресной форме они могут задавать начальный адрес как операнда, так и подпрограммы-оператора или подпрограммы-функции. Внутреннее двоичное представление формульного кода напоминает одноадресную систему команд. Каждая отдельная псевдокоманда (элементарная инструкция) отвечает одному символу операторно-формульного кода и состоит из поля-определителя, содержащего код-определитель, подобный коду операции, и, возможно, единственного поля операнда (рис.3). Псевдокоманды подразделяются на адресно-литеральные и структурные ограничители, не содержащие поля операнда. Структурные ограничители выполняют роль символов-ограничителей (знаки операций, скобки, знаки-разделители, привилегированные операторы), а адресно-литеральные псевдокоманды соответствуют константам, переменным либо именам операторов и функций, т.е. составляют код оператора или функции. При этом поле операнда адресно-литеральной псевдокоманды может содержать непосредственно операнд арифметико-логической операции, либо адресную ссылку того или иного вида на такой операнд или на подпрограмму, отвечающую оператору или функции. В этих псевдокомандах поле-определитель задает формат операнда и способ его адресации. Пример возможной системы команд формульного процессора и тактовой схемы их выполнения был протестирован на реализуемость в программе-эмуляторе (табл.2 представляет часть соответствующей кодовой таблицы). Таблица 2 Структурные ограничители
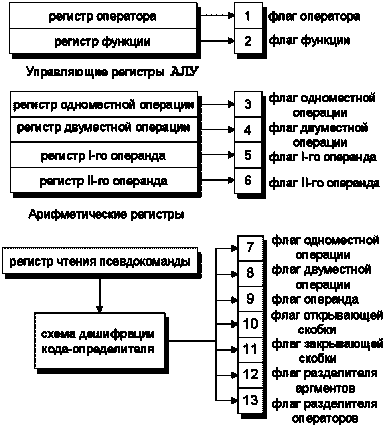
Сущность формульного процессора составляет зависимость выполнения команд от состояния загрузки регистров местной памяти. Для этого в качестве дополнительного звена в обычное подсоединение регистра чтения команды к устройству управления включается особый (главный) регистр автомата управления (РАУ; рис.2, 4), который также можно охарактеризовать как регистр формирователь-дешифратор кода команды управления. В роли этой команды выступает код, формируемый в РАУ в соответствии с состоянием загрузки регистров местной памяти и кодом очередной псевдокоманды (рис.4). Соответствие содержимого РАУ состоянию загрузки регистров местной памяти позволяет отслеживать текущее состояние вычислительного процесса и организовывать отработку очередного символа программы (т.е. очередной псевдокоманды) не только в зависимости от нее самой, но и от предшествующей части программы, выполнение которой создало данное состояние. Возможность соответствующего (однопросмотрового) алгоритма можно усмотреть, в частности, из общего «скобочного» принципа организации формульного вычисления: первой закрывается скобка (любого типа), которая была открыта последней. Иными словами, достаточно единственного (и даже общего) стека для адекватной организации сохранения промежуточных результатов. Подобным образом, оказывается достаточным малого числа информационных признаков (которыми выступают флаги загрузки регистров) для приведения зависимости вычисляющего алгоритма от общей структуры формулы к зависимости его фаз от этих признаков. В отличие от обычного набора универсальных регистров арифметические регистры формульного процессора в силу их соответствия флагам загрузки несколько более специализированы. Хотя их основным назначением по-прежнему является временное сохранение кодов операций и операндов, каждый из них ориентирован на сохранение своего вида элементов формульного кода, которым может быть код оператора, функции, одноместной или двуместной арифметико-логической операции или их операнды (рис.4). Таблица 3 Допустимые сочетания флагов загрузки арифметических регистров и их преобразования
В начальной фазе отработки очередного оператора РАУ находится в нулевом состоянии, а счетчик команд указывает на код текущей псевдокоманды, которая, при правильности формальной структуры программы, должна содержать код оператора. Выполнение этой «нулевой» (табл.3, первая строка) команды процессора состоит в переписывании кода оператора в регистр оператора, в силу чего соответственно переустанавливается флаг состояния его загрузки. Выборка последующей псевдокоманды завершает формирование новой команды управления. При загруженном регистре оператора процессор находится в режиме создания списка аргументов этого оператора. Этот режим завершается отработкой псевдокоманды, содержащей код разделителя операторов (флаг 13 на рис.4). К конечной фазе этой отработки в стеке (либо особо выделенных регистрах местной памяти) должны сформироваться адресно-литеральные псевдокоманды, представляющие вычисленные значения аргументов оператора, после чего инициируется выполнение данного оператора. При создании списка аргументов оператора процессор реализует вычисление соответствующих формульных выражений. Эти действия вытекают из логики обычного вычисления формулы и составляют наибольшее функциональное отличие формульного процессора от командного.
Рис. 4. Соответствие битов регистра автомата управления (РАУ) флагам загрузки регистров местной (внутрипроцессорной) памяти, предназначенных для сохранения и сборки кодов и операндов очередной выполняемой арифметико-логической операции Базовый состав системы команд формульного процессора, включая управляющие команды, коды арифметико-логических операций и коды режимов адресации вполне укладывается в привычную сотню кодов. Добавляемые команды управления сопоставимы по сложности с командами перехода по счетчику или прерывания на подпрограмму. Принципиально, имеется три схемы выполнения команд управления. 1 – сохранение кода очередного элемента программы в подходящем регистре местной памяти; 2 – сохранение содержимого регистров местной памяти в стеке, подобное сохранению управляющих регистров при выполнении команды прерывания; 3 – наиболее сложные команды включают сопоставление приоритетов арифметико-логических операций, соответствующих прочитанному элементу программы и сохраненному в местной памяти либо в стеке. В зависимости от результата, в одном случае дальнейшее выполнение команды состоит в сохранении кода и операндов откладываемой операции в местной памяти и/или стеке (т.е. развивается по схеме 1 или 2), в другом – включается процесс выполнения накопленных отложенных операций и соответствующего освобождения ячеек стека и регистров местной памяти. Таким образом, в результате, код арифметической или логической операции и ее операнды в формульном процессоре собираются при выполнении программы в арифметических регистрах из нескольких отдельных псевдокоманд и, возможно, результата выполнения предыдущей части программы, причем частью кода операции можно считать и код-определитель операнда, обеспечивающий извлечение из оперативной памяти в процессор данного, над которым производится действие. Выполнение арифметико-логических операций инициируется сигналами, вырабатываемыми при выполнении команд управления, а коды и операнды в момент инициирования находятся в соответствующих регистрах местной памяти. Заключение Формульный процессор, на наш взгляд, представляет собой систему с наиболее адекватным распределением функций между исполняющей схемой и программными системами низкого уровня (трансляторы, операционные системы и т.п.). Сохраняя уровень сложности и быстродействия, соответствующие обычным распространенным командным процессорам, формульный процессор позволяет не только разгрузить и упростить низкоуровневое программирование, но и значительно повысить общую прозрачность вычислительного процесса и контролируемость выполняемой программы. Дополнительным аргументом в пользу формульного подхода может служить характеристика соответствующего операторно-формульного кода как наиболее естественной и универсальной формы представления математических объектов алгоритмической природы, что создает основание и возможность для разработки соответствующих операторных кодовых стандартов, подобных таблице символов ASCII. Список литературы AndersonJ.P. A Computer for Direct Execution of Algorithmic Languages // Proc. EICC AFIPS, 20: Computers – Key to Total Systems Control. 1961. P.184. Вычислительные машины с развитыми системами интерпретации. Под ред. В.М.Глушкова. Киев: Наукова Думка, 1970, 259с. БулавенкоО.Н., ЯкубаА.А. Особенности архитектуры ЭВМ, реализующей языки высокого уровня и проектирование систем их интерпретации. Киев: Знание, 1986, 16с. ОрганикЭ. Организация системы ИНТЕЛ 432. М.: Мир, 1987, 446с. DijkstraE.W. // Communication ACM, 1968. V.11. №3, p.147. КотовВ.Е., СабельфельдВ.К. Теория схем программ. М.: Наука, 1991, 248c. Ляпунов А.А.В сб.: Проблемы кибернетики. Вып.1. М.: Физматгиз, 1958, с. 5. ЯновЮ.И. В сб.: Проблемы кибернетики. Вып.1. М.: Физматгиз, 1958, с. 75. КриницкийН.А., МироновГ.А., ФроловГ.Д. Программирование и алгоритмические языки. М.: Наука, 1975, 496с. КонП. Универсальная алгебра. М.: Мир, 1968, 351c. КозловМ.К. Формульный процессор с командоподобными логическими управляющими элементами. Патент РФ на изобретение №2143726 // Опубликован 27.12.99 Бюл. №36. См. также публикацию ВОИС WO 9904333 от 28.01.1999г. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||