
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология и педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по информатике программированию
Краткое содержание произведений
Реферат: Морфологический анализ цветных (спектрозональных) изображений
Реферат: Морфологический анализ цветных (спектрозональных) изображений
Пытьев Ю.П.
Московский государственный университет, Москва, Россия
1. Введение
Хорошо известно, что изображения одной и той же сцены, полученные при различных условиях освещения и(или) измененных[1] оптических свойствах объектов могут отличаться радикально. Это обстоятельство порождает значительные трудности в прикладных задачах анализа и интерпретации изображений реальных сцен, в которых решение должно не зависеть от условий регистрации изображений. Речь идет, например, о задачах выделения неизвестного объекта на фоне известной местности, известного объекта на произвольном фоне при неконтролируемых условиях освещения, о задаче совмещения изображенний одной и той же сцены, полученных в различных спектральных диапазонах и т.д.
Методы морфологического анализа, разработанные более десяти лет тому назад, [1-5], для решения перечисленных задач, были в основном ориентированы для применения к черно-белым изображениям[2] и оказались достаточно эффективными, [5-11].
Между тем, по меньшей мере два обстоятельства указывают на целесообразность разработки морфологических методов анализа цветных изображений. Во-первых, в задаче обнаружения и выделения объекта последний, как правило, прежде всего цветом отличается от фона. Во-вторых, описание формы изображения в терминах цвета позволит практически устранить эффект теней и влияние неопределенности в пространственном распределении интенсивности спектрально однородного освещения.
2. Цвет и яркость спектозонального изображения.
Рассмотрим
некоторые аспекты теории цвета так называемых многоспектральных
(спектрозональных, [13]) изображений, аналогичной классической колориметрии
[12]. Будем считать заданными n детекторов излучения со спектральными
чувствительностями ![]() j=1,2,...,n,
где l(0,¥) - длина волны излучения. Их выходные сигналы, отвечающие потоку
излучения со спектральной плотностью e(l)0, lÎ(0,¥), далее называемой излучением, образуют вектор
j=1,2,...,n,
где l(0,¥) - длина волны излучения. Их выходные сигналы, отвечающие потоку
излучения со спектральной плотностью e(l)0, lÎ(0,¥), далее называемой излучением, образуют вектор ![]() , w(×)=
, w(×)=![]() . Определим суммарную
спектральную чувствительность детекторов
. Определим суммарную
спектральную чувствительность детекторов ![]() ,
lÎ(0,¥), и соответствующий суммарный сигнал
,
lÎ(0,¥), и соответствующий суммарный сигнал 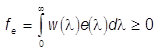 назовем
яркостью излучения e(×). Вектор
назовем
яркостью излучения e(×). Вектор ![]() назовем цветом излучения
e(×). Если
назовем цветом излучения
e(×). Если ![]() цвет e(×) и само
излучение назовем черным. Поскольку равенства
цвет e(×) и само
излучение назовем черным. Поскольку равенства ![]() и
и ![]() эквивалентны, равенство
эквивалентны, равенство ![]() имеет смысл и для черного
цвета, причем в этом случае
имеет смысл и для черного
цвета, причем в этом случае ![]() -
произвольный вектор, яркость оторого равна единице. Излучение e(×) назовем
белым и его цвет обозначим
-
произвольный вектор, яркость оторого равна единице. Излучение e(×) назовем
белым и его цвет обозначим ![]() если
отвечающие ему выходные сигналы всех детекторов одинаковы:
если
отвечающие ему выходные сигналы всех детекторов одинаковы:
![]() .
.
Векторы ![]() , и
, и ![]() ,
, ![]() , удобно считать элементами n-мерного
линейного пространства
, удобно считать элементами n-мерного
линейного пространства ![]() . Векторы fe,
соответствующие различным излучениям e(×), содержатся в
конусе
. Векторы fe,
соответствующие различным излучениям e(×), содержатся в
конусе ![]()
![]() .
Концы векторов
.
Концы векторов ![]() содержатся в
множестве
содержатся в
множестве ![]() , где Ï -
гиперплоскость
, где Ï -
гиперплоскость ![]() .
.
Далее предполагается, что всякое
излучение ![]() , где E - выпуклый конус
излучений, содержащий вместе с любыми излучениями
, где E - выпуклый конус
излучений, содержащий вместе с любыми излучениями ![]() все
их выпуклые комбинации (смеси)
все
их выпуклые комбинации (смеси) ![]() Поэтому
векторы
Поэтому
векторы ![]() в
в ![]() образуют выпуклый конус
образуют выпуклый конус ![]() , а векторы
, а векторы ![]() .
.
Если ![]() то и их аддитивная смесь
то и их аддитивная смесь
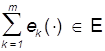 . Для нее
. Для нее
![]()
![]()
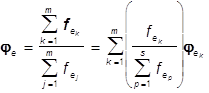 . (1)
. (1)
Отсюда следует
Лемма 1. Яркость fe и цвет je любой аддитивной смеси e(×) излучений e1(×),...,em(×), m=1,2,... определяются яркостями и цветами слагаемых.
Подчеркнем,
что равенство ![]() , означающее
факт совпадения яркости и цвета излучений e(×) и
, означающее
факт совпадения яркости и цвета излучений e(×) и ![]() , как правило, содержит
сравнительно небольшую информацию об их относительном спектральном составе.
Однако замена e(×) на
, как правило, содержит
сравнительно небольшую информацию об их относительном спектральном составе.
Однако замена e(×) на ![]() в любой
аддитивной смеси излучений не изменит ни цвета, ни яркости последней.
в любой
аддитивной смеси излучений не изменит ни цвета, ни яркости последней.
Далее
предполагается, что вектор w(×) таков, что в E можно указать базовые
излучения ![]() , для которых векторы
, для которых векторы ![]() , j=1,...,n,
линейно независимы. Поскольку цвет таких излучений непременно отличен от
черного, их яркости будем считать единичными,
, j=1,...,n,
линейно независимы. Поскольку цвет таких излучений непременно отличен от
черного, их яркости будем считать единичными, ![]() , j=1,...,n. В
таком случае излучение
, j=1,...,n. В
таком случае излучение ![]() характеризуется
лишь цветом
характеризуется
лишь цветом ![]() , j=1,...,n.
, j=1,...,n.
Для всякого излучения e(×) можно записать разложение
![]() , (1*)
, (1*)
в котором ![]() -
координаты
-
координаты ![]() в базисе
в базисе ![]() ,
,
или, в виде выходных
сигналов детекторов излучения, - ![]() , где
, где ![]() ,
, ![]() , - выходной сигнал i-го
детектора, отвечающий j-ому излучению ej(×), i, j=1,...,n. Матрица
, - выходной сигнал i-го
детектора, отвечающий j-ому излучению ej(×), i, j=1,...,n. Матрица ![]() - стохастическая, поскольку
ее матричные элементы как яркости базовых излучений
- стохастическая, поскольку
ее матричные элементы как яркости базовых излучений ![]() неотрицательны
и
неотрицательны
и ![]() , j=1,...,n.
При этом яркость
, j=1,...,n.
При этом яркость ![]() и вектор цвета
и вектор цвета ![]() ,
, 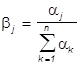 , j=1,...,n,
(конец которого лежит в Ï) определяются координатами aj и цветами излучений
, j=1,...,n,
(конец которого лежит в Ï) определяются координатами aj и цветами излучений ![]() , j=1,...,n,
и не зависят непосредственно от спектрального состава излучения e(×).
, j=1,...,n,
и не зависят непосредственно от спектрального состава излучения e(×).
В ряде
случаев белое излучение естественно определять исходя из базовых излучений, а
не из выходных сигналов детекторов, считая белым всякое излучение, которому в
(1*) отвечают равные координаты: ![]() .
.
Заметим,
что слагаемые в (1*), у которых aj<0,[3]
физически интерпретируются как соответствующие излучениям,
"помещенным" в левую часть равенства (1*) с коэффициентами -aj>0: ![]() . В такой
форме равенство (1*) представляет “баланс излучений”.
. В такой
форме равенство (1*) представляет “баланс излучений”.
Определим
в ![]() скалярное произведение
скалярное произведение ![]() и векторы
и векторы ![]() , биортогонально сопряженные
с
, биортогонально сопряженные
с ![]() :
: ![]() , i,j=1,...,n.
, i,j=1,...,n.
Лемма
2. В разложении (1*) ![]() , j=1,...,n,
, j=1,...,n,
![]() . Яркость
. Яркость ![]() , где
, где ![]() , причем вектор y ортогонален гиперплоскости Ï, так как
, причем вектор y ортогонален гиперплоскости Ï, так как ![]() , i,j=1,...,n.
, i,j=1,...,n.
Что касается скалярного проиведения ![]() , то его естественно
определять так, чтобы выходные сигналы детекторов
, то его естественно
определять так, чтобы выходные сигналы детекторов ![]() были координатами fe
в некотором ортонормированном базисе
были координатами fe
в некотором ортонормированном базисе ![]() .
В этом базисе конус
.
В этом базисе конус ![]() . Заметим, что для
любых векторов
. Заметим, что для
любых векторов ![]() и, тем более, для
и, тем более, для
![]() ,
, ![]() [4].
[4].
Пусть Х - поле зрения,
например, ограниченная область на плоскости R2, или на сетке ![]() ,
, ![]() спектральная
чувствительность j-го детектора излучения, расположенного в точке
спектральная
чувствительность j-го детектора излучения, расположенного в точке ![]()
![]() ;
;
![]() - излучение, попадающее в
точку
- излучение, попадающее в
точку ![]() . Изображением назовем
векторнозначную функцию
. Изображением назовем
векторнозначную функцию ![]()
![]() (2**)
(2**)
Точнее, пусть Х - поле зрения, (Х,
С, m) - измеримое пространство Х с мерой m, C - s-алгебра
подмножеств X. Цветное (спектрозональное) изображение ![]() определим равенством
определим равенством
![]() , (2)
, (2)
в котором почти для всех ![]() ,
, ![]() , - m-измеримые
функции на поле зрения X, такие, что
, - m-измеримые
функции на поле зрения X, такие, что
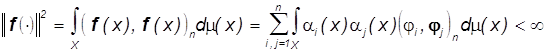 .
.
Цветные изображения образуют подкласс функций ![]() лебеговского класса
лебеговского класса ![]() функций
функций ![]() . Класс цветных изображений
обозначим LE,n.
. Класс цветных изображений
обозначим LE,n.
Впрочем,
для упрощения терминологии далее любой элемент ![]() называется
цветным изображением, а условие
называется
цветным изображением, а условие
![]() (2*)
(2*)
условием физичности изображений f(×).
Если f(×) - цветное изображение (2), то ![]() ,
как нетрудно проверить, - черно-белое изображение [2], т.е.
,
как нетрудно проверить, - черно-белое изображение [2], т.е. 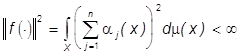 ,
, ![]() . Изображение
. Изображение ![]() , назовем черно-белым
вариантом цветного изображения f(×), а цветное изображение
, назовем черно-белым
вариантом цветного изображения f(×), а цветное изображение ![]() , f(x)0, xÎX - цветом изображения f(×). В точках
множества Â={xÎX: f(x)=0} черного цвета j(x),
xÎÂ, -
произвольные векторы из
, f(x)0, xÎX - цветом изображения f(×). В точках
множества Â={xÎX: f(x)=0} черного цвета j(x),
xÎÂ, -
произвольные векторы из ![]() ,
удовлетворяющие условию: яркость j(x)=1. Черно-белым вариантом
цветного изображения f(×) будем также
называть цветное изображение b(×), имеющее в каждой
точке Х ту же яркость, что и f(×), b(x)=f(x),
xÎX, и белый цвет, b(x)=b(x)/b(x)=b, xÎX.
,
удовлетворяющие условию: яркость j(x)=1. Черно-белым вариантом
цветного изображения f(×) будем также
называть цветное изображение b(×), имеющее в каждой
точке Х ту же яркость, что и f(×), b(x)=f(x),
xÎX, и белый цвет, b(x)=b(x)/b(x)=b, xÎX.
3. Форма цветного изображения.
Понятие формы изображения
призвано охарактеризовать форму изображенных объектов в терминах характерности
изображений, инвариантных относительно определенного класса преобразований
изображения, моделирующих меняющиеся условия его регистрации. Например, довольно
часто может меняться освещение сцены, в частности, при практически неизменном
спектральном составе может радикально изменяться распределение интенсивности
освещения сцены. Такие изменения освещения в формуле (2**) выражаются
преобразованием ![]() , в котором
множитель k(x) модулирует яркость изображения
, в котором
множитель k(x) модулирует яркость изображения ![]() в каждой точке
в каждой точке ![]() при неизменном распределении
цвета. При этом в каждой точке
при неизменном распределении
цвета. При этом в каждой точке ![]() у вектора
f(x) может измениться длина, но направление останется
неизменным.
у вектора
f(x) может измениться длина, но направление останется
неизменным.
Нередко изменение
распределения интенсивности освещения сопровождается значительным изменением и
его спектрального состава, но - пространственно однородным, одним и тем же в
пределах всей изображаемой сцены. Поскольку между спектром излучения e и
цветом j нет взаимно
однозначного соответствия, модель сопутствующего преобразования изображения f(x)
в терминах преобразования его цвета j(×). Для этого определим отображение A(×):![]() ,
ставящее в соответствие каждому вектору цвета
,
ставящее в соответствие каждому вектору цвета ![]() подмножество
поля зрения
подмножество
поля зрения ![]() в точках которого
изображение
в точках которого
изображение ![]() , имеет постоянный цвет
, имеет постоянный цвет ![]() .
.
Пусть при рассматриваемом
изменении освещения ![]() и, соответственно,
и, соответственно,
![]() ;
предлагаемая модель преобразования изображения состоит в том, что цвет
;
предлагаемая модель преобразования изображения состоит в том, что цвет ![]() преобразованного
изображения должен быть также постоянным на каждом множестве A(j), хотя, вообще
говоря, - другим, отличным от j.
Характекрным в данном случае является тот факт, что равенство
преобразованного
изображения должен быть также постоянным на каждом множестве A(j), хотя, вообще
говоря, - другим, отличным от j.
Характекрным в данном случае является тот факт, что равенство ![]() влечет
влечет ![]() . Если
. Если ![]() - самое детальное
изображение сцены, то, вообще говоря, на различных множествах A(j¢) и A(j) цвет изображения
- самое детальное
изображение сцены, то, вообще говоря, на различных множествах A(j¢) и A(j) цвет изображения ![]() может
оказаться одинаковым[5].
может
оказаться одинаковым[5].
Как правило, следует учитывать непостоянство оптических характеристик сцены и т.д. Во всех случаях форма изображения должна быть инвариантна относительно преобразования из выделенного класса и, более того, должна определять изображение с точностью до произвольного преобразования из этого класса.
Для определения понятия
формы цветного изображения f(×) на ![]() удобно
ввести частичный порядок p , т.е.
бинарное отношение, удовлетворяющее условиям: 1)
удобно
ввести частичный порядок p , т.е.
бинарное отношение, удовлетворяющее условиям: 1)![]() ,
2)
,
2) ![]() ,
, ![]() , то
, то ![]() ,
, ![]() ; отношение p должно быть согласованным с
определением цветного изображения (с условием физичности), а именно,
; отношение p должно быть согласованным с
определением цветного изображения (с условием физичности), а именно, ![]() , если
, если ![]() . Отношение p интерпретируется аналогично тому, как
это принято в черно-белой морфологии[2], а именно,
. Отношение p интерпретируется аналогично тому, как
это принято в черно-белой морфологии[2], а именно, ![]() означает,
что изображения f(×) и g(×) сравнимы по форме, причем форма
g(×) не сложнее, чем
форма f(×). Если
означает,
что изображения f(×) и g(×) сравнимы по форме, причем форма
g(×) не сложнее, чем
форма f(×). Если
![]() и
и ![]() , то f(×) и g(×) назовем совпадающими по
форме (изоморфными), f(×)
~ g(×). Например, если f(×) и g(×) - изображения одной и той же
сцены, то g(×),
грубо говоря, характеризует форму изображенных объектов не точнее (подробнее,
детальнее), чем f (×),
если
, то f(×) и g(×) назовем совпадающими по
форме (изоморфными), f(×)
~ g(×). Например, если f(×) и g(×) - изображения одной и той же
сцены, то g(×),
грубо говоря, характеризует форму изображенных объектов не точнее (подробнее,
детальнее), чем f (×),
если ![]() .
.
В рассматриваемом выше
примере преобразования изображений ![]() , если между множествами A(j),
, если между множествами A(j),![]() и A¢(j¢),
и A¢(j¢),![]() существует
взаимно-однозначное соответствие, т.е., если существует функция
существует
взаимно-однозначное соответствие, т.е., если существует функция ![]() , такая, что A¢(j¢(j))= A(j),
, такая, что A¢(j¢(j))= A(j),![]() , причем
, причем![]() , если
, если ![]() . В этом случае равенства
. В этом случае равенства ![]() и
и ![]() эквивалентны,
эквивалентны, ![]() и
и ![]() изоморфны и одинаково
детально характеризуют сцену, хотя и в разных цветах.
изоморфны и одинаково
детально характеризуют сцену, хотя и в разных цветах.
Если же ![]() не взаимно однозначно, то A¢(j¢)=U
A(j) и
не взаимно однозначно, то A¢(j¢)=U
A(j) и ![]() . В этом случае
равенство
. В этом случае
равенство ![]() влечет
влечет ![]() (но не эквивалентно)
(но не эквивалентно) ![]() ,
, ![]() передает, вообще говоря, не
все детали сцены, представленные в
передает, вообще говоря, не
все детали сцены, представленные в ![]() .
.
Пусть, скажем, g(×) - черно-белый вариант f(×), т.е. g(x)=f(x) и g(x)/g(x)=b, xÎX.
Если преобразование ![]() -
следствие изменившихся условий регистрации изображения, то, естественно,
-
следствие изменившихся условий регистрации изображения, то, естественно, ![]() . Аналогично, если f(×), g(×) -
изображения одной и той же сцены, но в g(×),
вследствие неисправности выходные сигналы некоторых датчиков равны нулю,
то
. Аналогично, если f(×), g(×) -
изображения одной и той же сцены, но в g(×),
вследствие неисправности выходные сигналы некоторых датчиков равны нулю,
то ![]() . Пусть F - некоторая полугруппа
преобразований
. Пусть F - некоторая полугруппа
преобразований ![]() , тогда для любого
преобразования FÎF
, тогда для любого
преобразования FÎF ![]() ,
поскольку, если некоторые детали формы объекта не отражены в изображении f(×), то они, тем более, не
будут отражены в g(×).
,
поскольку, если некоторые детали формы объекта не отражены в изображении f(×), то они, тем более, не
будут отражены в g(×).
Формой ![]() изображения f(×) назовем множество
изображений
изображения f(×) назовем множество
изображений ![]() , форма которых не сложнее,
чем форма f`(×),
и их пределов в
, форма которых не сложнее,
чем форма f`(×),
и их пределов в ![]() (черта
символизирует замыкание в
(черта
символизирует замыкание в ![]() ). Формой
изображения f(×) в
широком смысле назовем минимальное линейное подпространство
). Формой
изображения f(×) в
широком смысле назовем минимальное линейное подпространство ![]() , содержащее
, содержащее ![]() . Если считать, что
. Если считать, что ![]() для любого изображения
для любого изображения ![]() , то это будет означать,
что отношение p непрерывно
относительно сходимости в
, то это будет означать,
что отношение p непрерывно
относительно сходимости в ![]() в том
смысле, что
в том
смысле, что ![]() .
.
Рассмотрим теперь более подробно понятие формы для некоторых характерных классов изображений и их преобразований.
4. Форма кусочно-постоянного (мозаичного) цветного изображения.
Во многих практически
важных задачах форма объекта на изображении может быть охарактеризована
специальной структурой излучения, достигающего поле зрения X в виде ![]() здесь
здесь ![]() - индикаторные функции
непересекающихся подмножеств Аi, i=1,…...,N, положительной
меры поля зрения Х, на каждом из которых функции
- индикаторные функции
непересекающихся подмножеств Аi, i=1,…...,N, положительной
меры поля зрения Х, на каждом из которых функции 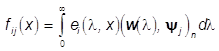 ,
, ![]() , j=1,...,n, i=1,...,N,
непрерывны. Поскольку согласно лемме 2
, j=1,...,n, i=1,...,N,
непрерывны. Поскольку согласно лемме 2
![]()
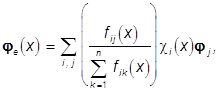
![]() , (3)
, (3)
то цветное изображение fe(×), такого объекта
характеризует его форму непрерывным распределением яркости и цвета на
каждом подмножестве Ai, i=1,...,N. Для
изображения ![]() ,
, ![]() где
где ![]() , также характерно
напрерывное распределение яркости и цвета на каждом Ai, если
, также характерно
напрерывное распределение яркости и цвета на каждом Ai, если ![]() , - непрерывные функции.
, - непрерывные функции.
Если, в частности, цвет и яркость ![]() постоянны на Ai,
i=1,...,N, то это верно и для всякого изображения
постоянны на Ai,
i=1,...,N, то это верно и для всякого изображения ![]() , если
, если ![]() не зависит явно от
не зависит явно от ![]() . Для такого
изображения примем следующее представление:
. Для такого
изображения примем следующее представление:
![]() , (4)
, (4)
его черно-белый вариант
![]() (4*)
(4*)
на каждом Ai имеет
постоянную яркость ![]() , и цвет
изображения (4)
, и цвет
изображения (4)
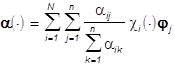 (4**)
(4**)
не меняется на Ai
и равен 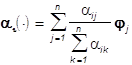 , i=1,...,N.
, i=1,...,N.
Поскольку для реальных
изображений должно быть выполнено условие физичности (2*), ![]() , то форму изображения
(4), имеющего на различных множествах Аi имеет несовпадающие
яркости
, то форму изображения
(4), имеющего на различных множествах Аi имеет несовпадающие
яркости ![]() и различные цвета
и различные цвета 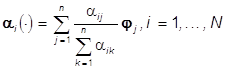 , определим как выпуклый
замкнутый в
, определим как выпуклый
замкнутый в ![]() конус:
конус:
![]()
![]() . (4***)
. (4***)
v(a), очевидно, содержится в n×N мерном линейном подпространстве
![]()
![]() , (4****)
, (4****)
которое назовем формой a(×) в широком смысле.
Форму в широком смысле
любого изображения a(×),
у которого не обязательно различны яркости и цвета на различных
подмножествах Ai ,i=1,...,N, определим как линейное
подпространство ![]() , натянутое не вектор-функции Fa(×),FÎF,
где F - класс преобразований
, натянутое не вектор-функции Fa(×),FÎF,
где F - класс преобразований ![]() ,
определенных как преобразования векторов a(x)®Fa(x) во
всех точках xÎX;
здесь F - любое преобразование
,
определенных как преобразования векторов a(x)®Fa(x) во
всех точках xÎX;
здесь F - любое преобразование ![]() . Тот факт, что F означает как преобразование
. Тот факт, что F означает как преобразование ![]() , так и преобразование
, так и преобразование ![]() , не должен вызывать
недоразумения.
, не должен вызывать
недоразумения.
Изображения из конуса(4***) имеют форму, которая не сложнее, чем форма a(×) (4), поскольку некоторые из них могут иметь одно и то же значение яркости или(и) цвета на различных множествах Аi, i=1,…………..,N. Также множества оказываются, по существу, объединенными в одно, что и приводит к упрощению формы изображения, поскольку оно отражает меньше деталей формы изображенного объекта, чем изображение (4). Это замечание касается и L(a(×)), если речь идет о форме в широком смысле.
Лемма 3. Пусть {Аi}
- измеримое разбиение X: ![]() .
.
Изображение (3) имеет на каждом подмножестве Ai :
- постоянную яркость
![]() и цвет
и цвет ![]() , если и только если
выполняется равенство (4);
, если и только если
выполняется равенство (4);
- постоянный цвет ![]() , если и только если в
(3)
, если и только если в
(3) ![]() ;
;
- постоянную яркость
fi , i=1,...,N, если и только если в (3) ![]() не зависит от
не зависит от
![]() , i=1,…...,N.
, i=1,…...,N.
Доказательство . На множестве Ai яркость и цвет изображения (3) равны соответственно[6]
![]() ,
,
![]() , i=1,.…..,N.
, i=1,.…..,N.
Если выполнено равенство (4), то ![]() и
и ![]() от
от ![]() не зависят. Наоборот, если
не зависят. Наоборот, если ![]() и
и ![]() , то и
, то и ![]() , т.е. выполняется (4).
, т.е. выполняется (4).
Если ![]() , то
цвет
, то
цвет ![]() не зависит от
не зависит от ![]() . Наоборот, пусть
. Наоборот, пусть ![]() не зависит от
не зависит от ![]() . В силу линейной
независимости
. В силу линейной
независимости ![]() координаты j(i)(x) не
зависят от
координаты j(i)(x) не
зависят от ![]() , т.е.
, т.е. ![]() и, следовательно,
и, следовательно, ![]() где
где ![]() - яркость на A i
и
- яркость на A i
и ![]() . Последнее утверждение
очевидно n
. Последнее утверждение
очевидно n
Цвет изображения определяется как электродинамическими свойствами поверхности изображенного объекта, так и спектральным составом облучающего электромагнитного излучения в том диапазоне, который используется для регистрации изображения. Речь идет о спектральном составе излучения, покидающего поверхность объекта и содержащего как рассеянное так и собственное излучения объекта. Поскольку спектральный состав падающего излучения, как правило, пространственно однороден, можно считать, что цвет изображения несет информацию о свойствах поверхности объекта, о ее форме, а яркость в значительной степени зависит и от условий “освещения”. Поэтому на практике в задачах морфологического анализа цветных изображений сцен важное значение имеет понятие формы изображения, имеющего постоянный цвет и произвольное распределение яркости в пределах заданных подмножеств Ai , i=1,...,N, поля зрения X.
Итак, пусть в согласии с леммой 3
![]() , (5)
, (5)
где, ![]() - индикаторная
функция Ai,
- индикаторная
функция Ai, ![]() , функция
gi(×)
задает распределение яркости
, функция
gi(×)
задает распределение яркости
![]() (6)
(6)
в пределах Ai при постоянном цвете
![]() ,
i=1,...,N, (7)
,
i=1,...,N, (7)
причем для изображения (5) цвета j(i), i=1,.…..,N,
считаются попарно различными, а функции g(i), i=1,.…..,N, -
удовлетворяющими условиям ![]() i=1,.…..,N.
i=1,.…..,N.
Нетрудно заметить, что в выражениях (5),(6) и (7) без
потери общности можно принять условие нормировки ![]() ,
позволяющее упростить выражения (6) и (7) для распределений яркости и цвета. С
учетом нормировки распределение яркости на Ai задается
функцией
,
позволяющее упростить выражения (6) и (7) для распределений яркости и цвета. С
учетом нормировки распределение яркости на Ai задается
функцией ![]() а цвет на Ai
равен
а цвет на Ai
равен
![]() (7*)
(7*)
Форму изображения (5) определим как класс всех изображений
![]() (8)
(8)
![]() ,
,
каждое из которых, как и изображение (5), имеет
постоянный цвет в пределах каждого Ai, i=1,...,N. Форма таких
изображений не сложнее, чем форма f(×) (5), поскольку в
изображении ![]() на некоторых различных
подмножествах Ai, i=1,...,N, могут совпадать значения цвета,
которые непременрно различны в изображении f(×) (5). Совпадение
цвета
на некоторых различных
подмножествах Ai, i=1,...,N, могут совпадать значения цвета,
которые непременрно различны в изображении f(×) (5). Совпадение
цвета ![]() на различных подмножествах Ai,
i=1,...,N ведет к упрощению формы изображения
на различных подмножествах Ai,
i=1,...,N ведет к упрощению формы изображения ![]() по
сравнению с формой f(×) (5). Все изображения
по
сравнению с формой f(×) (5). Все изображения ![]() , имеющие различный цвет на
различных Ai, i=1,...,N, считаются изоморфными f(×) (и между собой), форма
остальных не сложнее, чем форма f(×). Если
, имеющие различный цвет на
различных Ai, i=1,...,N, считаются изоморфными f(×) (и между собой), форма
остальных не сложнее, чем форма f(×). Если ![]() , то, очевидно,
, то, очевидно, ![]() .
.
Если в (8) яркость ![]() , то цвет
, то цвет ![]() на Ai
считается произвольным (постоянным), если же
на Ai
считается произвольным (постоянным), если же ![]() в
точках некоторого подмножества
в
точках некоторого подмножества ![]() , то
цвет
, то
цвет ![]() на Ai
считается равным цвету
на Ai
считается равным цвету ![]() на
на ![]() , i=1,...,N.
, i=1,...,N.
Цвет изображения (8) может не совпадать с цветом (5).
Если же по условию задачи все изображения ![]() ,
форма которых не сложнее, чем форма
,
форма которых не сложнее, чем форма ![]() , должны
иметь на Ai, i=1,...,N, тот же цвет, что и у
, должны
иметь на Ai, i=1,...,N, тот же цвет, что и у ![]() то следует потребовать,
чтобы
то следует потребовать,
чтобы ![]() , в то время, как яркости
, в то время, как яркости ![]() остаются
произвольными (если
остаются
произвольными (если ![]() , то цвет
, то цвет ![]() на Ai
определяется равным цвету f(×) на Ai,
i=1,...,N).
на Ai
определяется равным цвету f(×) на Ai,
i=1,...,N).
Нетрудно определить форму любого, не обязательно
мозаичного, изображения f(×) в том случае, когда допустимы произвольные
изменения яркости ![]() при неизменном
цвете j(x) в каждой точке
при неизменном
цвете j(x) в каждой точке
![]() . Множество, содержащее все
такие изображения
. Множество, содержащее все
такие изображения
![]() (9)
(9)
назовем формой в широком смысле изображения ![]() , у которого f(x)¹0, m-почти
для всех
, у которого f(x)¹0, m-почти
для всех ![]() , [ср. 2].
, [ср. 2]. ![]() является линейным
подпространством
является линейным
подпространством ![]() , содержащем любую
форму
, содержащем любую
форму
![]() , (10)
, (10)
в которой включение ![]() определяет
допустимые значения яркости. В частности, если
определяет
допустимые значения яркости. В частности, если ![]() означает,
что яркость неотрицательна:
означает,
что яркость неотрицательна: ![]() , то
, то ![]() - выпуклый замкнутый конус
в
- выпуклый замкнутый конус
в ![]() , принадлежащий
, принадлежащий ![]() .
.
Более удобное описание формы изображения может быть получено на основе методов аппроксимации цветных изображений, в которых форма определяется как оператор наилучшего приближения. В следующем параграфе дано представление формы изображения в виде оператора наилучшего приближения.
5. Задачи аппроксимации цветных изображений. Форма как оператор наилучшего приближения.
Рассмотрим вначале задачи
приближения кусочно-постоянными (мозаичными) изображениями. Решение этих задач
позволит построить форму изображения ![]() в том
случае, когда считается, что
в том
случае, когда считается, что ![]() для
любого преобразования
для
любого преобразования ![]() , действующего на
изображение
, действующего на
изображение ![]() как на вектор
как на вектор ![]() в каждой точке
в каждой точке ![]() и оставляющего
и оставляющего ![]() элементом
элементом ![]() , т.е. изображением. Форма в
широком смысле
, т.е. изображением. Форма в
широком смысле ![]() определяется как
оператор
определяется как
оператор ![]() наилучшего приближения
изображения
наилучшего приближения
изображения ![]() изображениями
изображениями ![]()
![]()
где ![]() - класс
преобразований
- класс
преобразований ![]() , такой, что
, такой, что ![]() . Иначе можно считать, что
. Иначе можно считать, что
![]() (10*)
(10*)
а ![]() -
оператор наилучшего приближения элементами множества
-
оператор наилучшего приближения элементами множества ![]() , форма которых не сложнее,
чем форма
, форма которых не сложнее,
чем форма ![]() . Характеристическим для
. Характеристическим для ![]() является тот факт, что,
если f(x)=f(y), то для любого
является тот факт, что,
если f(x)=f(y), то для любого ![]() .
.
5.1. Приближение цветного изображения изображениями, цвет и
яркость которых постоянны на подмножествах разбиения ![]() поля зрения X.
поля зрения X.
Задано разбиение ![]() , требуется
определить яркость и цвет наилучшего приближения на каждом
, требуется
определить яркость и цвет наилучшего приближения на каждом ![]() . Рассмотрим задачу наилучшего приближения в
. Рассмотрим задачу наилучшего приближения в ![]() цветного изображения f(×) (2) изображениями (4), в которых считается заданным разбиение
цветного изображения f(×) (2) изображениями (4), в которых считается заданным разбиение ![]() поля зрения X и
требуется определить
поля зрения X и
требуется определить ![]() из условия
из условия
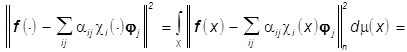
![]() (11)
(11)![]()
Теорема
1. Пусть ![]() .
Тогда решение задачи (11) имеет вид
.
Тогда решение задачи (11) имеет вид
![]() , i=1,...,N, j=1,...,n, (12)
, i=1,...,N, j=1,...,n, (12)
и искомое изображение (4) задается равенством
![]() . (13)
. (13)
Оператор ![]() является ортогональным
проектором на линейное подпространство (4****)
является ортогональным
проектором на линейное подпространство (4****) ![]() изображений (4),
яркости и цвета которых не изменяются в пределах
каждого Ai , i=1,...,N.
изображений (4),
яркости и цвета которых не изменяются в пределах
каждого Ai , i=1,...,N.
Черно-белый
вариант ![]() (4*) цветного
изображения
(4*) цветного
изображения ![]() (4) является
наилучшей в
(4) является
наилучшей в ![]() аппроксимацией черно-белого варианта
аппроксимацией черно-белого варианта ![]() цветного
изображения f(×) (2), если цветное изображение
цветного
изображения f(×) (2), если цветное изображение ![]() (4) является наилучшей в
(4) является наилучшей в
![]() аппроксимацией цветного
изображения f(×) (2). Оператор
аппроксимацией цветного
изображения f(×) (2). Оператор 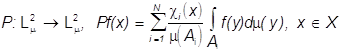 , является
ортогональным проектором на линейное подпространство черно-белых изображений,
яркость которых постоянна в пределах каждого
, является
ортогональным проектором на линейное подпространство черно-белых изображений,
яркость которых постоянна в пределах каждого ![]() .
.
В точках множества ![]() цвет
цвет 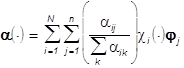 (4**) наилучшей
аппроксимации
(4**) наилучшей
аппроксимации ![]() (4) цветного
изображения f(×) (2) является цветом
аддитивной смеси составляющих f(×) излучений,
которые попадают на
(4) цветного
изображения f(×) (2) является цветом
аддитивной смеси составляющих f(×) излучений,
которые попадают на ![]() .
.
Доказательство. Равенства (12) - условия минимума положительно определенной
квадратичной формы (11), П - ортогональный проектор, поскольку в задаче
(11) наилучшая аппроксимация - ортогональная проекция f(×) на ![]() . Второе утверждение следует
из равенства
. Второе утверждение следует
из равенства
![]() ,
вытекающего из (13). Последнее утверждение следует из
равенств
,
вытекающего из (13). Последнее утверждение следует из
равенств
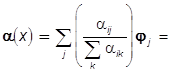
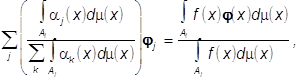
![]() ,i=1,...,N
вытекающих из (12) и равенства (1), в котором индекс k следует заменить
на xÎX. ■
,i=1,...,N
вытекающих из (12) и равенства (1), в котором индекс k следует заменить
на xÎX. ■
Замечание
1. Для любого измеримого разбиения ![]() ортогональные проекторы
ортогональные проекторы
![]() и
и ![]() определяют
соответственно форму в широком смысле цветного изображения (4), цвет и яркость которого, постоянные в пределах каждого
определяют
соответственно форму в широком смысле цветного изображения (4), цвет и яркость которого, постоянные в пределах каждого ![]() , различны для различных
, различны для различных ![]() , ибо
, ибо ![]() , и форму в широком
смысле черно-белого изображения, яркость которого постоянна на
каждом
, и форму в широком
смысле черно-белого изображения, яркость которого постоянна на
каждом ![]() и различна для разных
и различна для разных ![]() ,[2].
,[2].
Если
учесть, условие физичности (2*), то формой цветного изображения следует считать
проектор ![]() на
выпуклый замкнутый конус
на
выпуклый замкнутый конус ![]() (4***)
(4***)
Аналогично формой
черно-белого изображения следует считать проектор ![]() на
выпуклый замкнутый конус изображений (4*), таких, что
на
выпуклый замкнутый конус изображений (4*), таких, что ![]() [2]. Дело в том, что оператор
[2]. Дело в том, что оператор ![]() определяет
форму
определяет
форму ![]() изображения (4), а именно
изображения (4), а именно
![]() -
множество собственных функций оператора
-
множество собственных функций оператора ![]() . Поскольку
. Поскольку ![]() f(×) -
наилучшее приближение изображения
f(×) -
наилучшее приближение изображения ![]() изображениями из
изображениями из ![]() , для любого изображения
, для любого изображения ![]() из
из ![]() и только для таких
и только для таких ![]() -
- ![]() .
Поэтому проектор
.
Поэтому проектор ![]() можно
отождествить с формой изображения (4).
можно
отождествить с формой изображения (4).
Аналогично для черно-белого изображения a(×)
![]() ,[7]
[2]. И проектор
,[7]
[2]. И проектор ![]() можно
отождествить с формой изображения (4*), как это сделано в работах [2,3].
можно
отождествить с формой изображения (4*), как это сделано в работах [2,3].
Примечания.
Формы в
широком смысле не определяются связью задач наилучшего приближения элементами ![]() и
и ![]() , которая известна как
транзитивность проецирования. Именно, если
, которая известна как
транзитивность проецирования. Именно, если ![]() оператор
наилучшего в
оператор
наилучшего в ![]() приближения злементами
выпуклого замкнутого (в
приближения злементами
выпуклого замкнутого (в ![]() и в
и в ![]() ) конуса
) конуса ![]() , то
, то ![]() . Иначе говоря, для
определения наилучшего в
. Иначе говоря, для
определения наилучшего в ![]() приближения
приближения
![]() элементами
элементами ![]() можно вначале найти
ортогональную проекцию
можно вначале найти
ортогональную проекцию ![]() изображения
изображения ![]() на
на ![]() , а затем
, а затем ![]() спроецировать в
спроецировать в ![]() на
на ![]() . При этом конечномерный
проектор
. При этом конечномерный
проектор ![]() для каждого конкретного
конуса
для каждого конкретного
конуса ![]() может быть реализован
методом динамического программирования, а для многих задач морфологического
анализа изображений достаточным оказывается использование лишь проектора П
.
может быть реализован
методом динамического программирования, а для многих задач морфологического
анализа изображений достаточным оказывается использование лишь проектора П
.
Форма
в широком смысле ![]() (4***) изображения (4) полностью определяется измеримым разложением
(4***) изображения (4) полностью определяется измеримым разложением
![]() , последнее, в свою очередь
определяется изображением
, последнее, в свою очередь
определяется изображением
![]() ,
,
если векторы ![]() попарно
различны. Если при этом
попарно
различны. Если при этом ![]() , то
форма в широком смысле
, то
форма в широком смысле ![]() может быть
определена и как оператор П ортогонального проецирования на
может быть
определена и как оператор П ортогонального проецирования на ![]() , определенный равенством
(13).
, определенный равенством
(13).
Посмотрим, каким образом
воспользоваться этими фактами при построении формы в широком смысле как
оператора ортогонального проецирования на линейное подпространство ![]() (10*) для произвольного
изображения
(10*) для произвольного
изображения ![]() . Пусть
. Пусть ![]() - множество значений
- множество значений ![]() и
и ![]() - измеримое разбиение X , порожденное
- измеримое разбиение X , порожденное ![]() , в котором
, в котором ![]() - подмножество X , в пределах
которого изображение
- подмножество X , в пределах
которого изображение ![]() имеет постоянные
яркость и цвет, определяемые вектором
имеет постоянные
яркость и цвет, определяемые вектором ![]() ,
если
,
если ![]() .
.
Однако для найденного разбиения
условие ![]() , вообще говоря, невыполнимо
и, следовательно, теорема 1 не позволяет построить ортогональный проектор П
на
, вообще говоря, невыполнимо
и, следовательно, теорема 1 не позволяет построить ортогональный проектор П
на ![]() . Покажем, что П
можно получить как предел последовательности конечномерных ортогональных
проекторов. Заметим вначале, что любое изображение
. Покажем, что П
можно получить как предел последовательности конечномерных ортогональных
проекторов. Заметим вначале, что любое изображение ![]() можно
представить в виде предела (в
можно
представить в виде предела (в ![]() ) должным
образом организованной последовательности мозаичных изображений
) должным
образом организованной последовательности мозаичных изображений
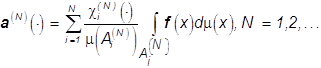 (*)
(*)
где ![]() -
индикатор множества
-
индикатор множества ![]() ,
принадлежащего измеримому разбиению
,
принадлежащего измеримому разбиению ![]()
В (*) можно, например, использовать так называемую исчерпывающую последовательность разбиений [], удовлетворяющую следующим условиям
- ![]() - C - измеримо,
- C - измеримо, ![]() ;
;
- N+1-oe разбиение является продолжением N-го,
т.е. для любого ![]() , найдется i=i(j),
, найдется i=i(j),![]() , такое, что
, такое, что ![]() ;
;
- минимальная s-алгебра, содержащая все ![]() , совпадает с C.
, совпадает с C.
Лемма (*). Пусть ![]() - исчерпывающая
последователь-ность разбиений X и
- исчерпывающая
последователь-ность разбиений X и ![]() - то
множество из
- то
множество из ![]() , которое содержит
, которое содержит ![]() . Тогда для любой C-измеримой
функции
. Тогда для любой C-измеримой
функции ![]()
![]()
и m-почти для всех ![]()
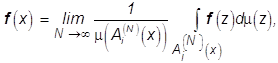 [
]. n
[
]. n
Воспользуемся этим результатом для
построения формы в широком смысле П произвольного изображения ![]() . Пусть
. Пусть ![]() - минимальная s-алгебра,
относительно которой измеримо
- минимальная s-алгебра,
относительно которой измеримо ![]() , т.е.
пусть
, т.е.
пусть ![]() , где
, где ![]() - прообраз борелевского
множества
- прообраз борелевского
множества ![]() , B - s-алгебра
борелевских множеств
, B - s-алгебра
борелевских множеств ![]() . Заменим в
условиях, определяющих исчерпывающую последовательность разбиений, C на
. Заменим в
условиях, определяющих исчерпывающую последовательность разбиений, C на ![]() и выберем эту, зависящую от
и выберем эту, зависящую от
![]() , исчерпывающую
последовательность (
, исчерпывающую
последовательность (![]() - измеримых) разбиений
в лемме (*).
- измеримых) разбиений
в лемме (*).
Теорема (*). Пусть ![]() ,
, ![]() - исчерпывающая
последовательность разбиений X, причем
- исчерпывающая
последовательность разбиений X, причем ![]() - минимальная
s-алгебра, содержащая все
- минимальная
s-алгебра, содержащая все ![]() и
П(N) - ортогональный проектор
и
П(N) - ортогональный проектор ![]() ,
определенный равенством
,
определенный равенством 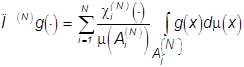 ,
, ![]()
Тогда
1) для любого ![]() -измеримого
изображения
-измеримого
изображения ![]() и почти для всех
и почти для всех ![]() ,
, ![]() ,
,
2) для любого изображения ![]() при
при ![]()
![]() (в
(в ![]() ), где П - ортогональный
проектор на
), где П - ортогональный
проектор на ![]() .
.
Доказательство. Первое утверждение
непосредственно следует из леммы (*) и определения ![]() .
Для доказательства второго утверждения заметим, что, так как A(N+1)
- продолжение разбиения A(N), N=1,2,..., то
последовательность проекторов П(N), N=1,2,..., монотонно
неубывает:
.
Для доказательства второго утверждения заметим, что, так как A(N+1)
- продолжение разбиения A(N), N=1,2,..., то
последовательность проекторов П(N), N=1,2,..., монотонно
неубывает: ![]() и потому сходится
(поточечно) к некоторому ортогональному проектору П. Так как
и потому сходится
(поточечно) к некоторому ортогональному проектору П. Так как ![]() - множество всех
- множество всех ![]() -измеримых изображений и их
пределов (в
-измеримых изображений и их
пределов (в ![]() ), а в силу
леммы (*) для любого
), а в силу
леммы (*) для любого ![]() -измеримого
изображения
-измеримого
изображения ![]()
![]() , то для
любого изображения
, то для
любого изображения ![]()
![]() и для любого
и для любого ![]()
![]() ,
ибо
,
ибо ![]() -измеримо, N=1,2,...
n
-измеримо, N=1,2,...
n
Вопрос о том, каким образом может быть построена исчерпывающая последовательность разбиений, обсуждается в следующем пункте.
Заданы
векторы f1,...,fq, требуется определить разбиение ![]() , на множествах которого
наилучшее приближение принимает соответственно значенния f1,...,fq.
Рассмотрим задачу приближения цветного
изображения f(×), в которой задано не разбиение
, на множествах которого
наилучшее приближение принимает соответственно значенния f1,...,fq.
Рассмотрим задачу приближения цветного
изображения f(×), в которой задано не разбиение ![]() поля зрения X, а
векторы
поля зрения X, а
векторы ![]() в
в ![]() , и требуется построить
измеримое разбиение
, и требуется построить
измеримое разбиение ![]() поля зрения,
такое, что цветное изображение
поля зрения,
такое, что цветное изображение ![]() -
наилучшая в
-
наилучшая в ![]() аппроксимация f(×). Так как
аппроксимация f(×). Так как
![]()
![]() , (14*)
, (14*)
то в Ai
следует отнести лишь те точки ![]() , для
которых
, для
которых ![]() ,
, ![]() =1,2,...,q, или, что
то же самое,
=1,2,...,q, или, что
то же самое, ![]()
![]() =1,2,...,q. Те точки,
которые согласно этому принципу могут быть отнесены к нескольким множествам,
должны быть отнесены к одному из них по произволу. Учитывая это, условимся
считать, что запись
=1,2,...,q. Те точки,
которые согласно этому принципу могут быть отнесены к нескольким множествам,
должны быть отнесены к одному из них по произволу. Учитывая это, условимся
считать, что запись
![]()
![]() , (14)
, (14)
означает, что
множества (14) не пересекаются и ![]() .
.
Чтобы
сформулировать этот результат в терминах морфологического анализа, рассмотрим
разбиение ![]() , в котором
, в котором
![]() (15)
(15)
и звездочка указывает
на договоренность, принятую в (14). Определим оператор F,
действующий из ![]() в
в ![]() по формуле
по формуле ![]() ,
, ![]() , i=1,...,q.
Очевидно, F всегда можно согласовать с (14) так, чтобы включения
, i=1,...,q.
Очевидно, F всегда можно согласовать с (14) так, чтобы включения ![]() и
и ![]() , i=1,...,q, можно было
считать эквивалентными. [8]
, i=1,...,q, можно было
считать эквивалентными. [8]
Теорема
2. Пусть ![]() - заданные векторы Rn. Решение задачи
- заданные векторы Rn. Решение задачи
![]()
наилучшего в ![]() приближения изображения f(×) изображениями
приближения изображения f(×) изображениями ![]() имеет вид
имеет вид ![]() , где
, где ![]() - индикаторная функция
множества
- индикаторная функция
множества ![]() . Множество
. Множество ![]() определено равенством (15).
Нелинейный оператор
определено равенством (15).
Нелинейный оператор ![]() , как всякий
оператор наилучшего приближения удовлетворяет условию F2=F, т.е.
является пректором.
, как всякий
оператор наилучшего приближения удовлетворяет условию F2=F, т.е.
является пректором.
Замечание
2. Если данные задачи доступны лишь в
черно-белом варианте, то есть заданы числа ![]() ,
i=1,...,q, которые можно считать упорядоченными согласно условию
,
i=1,...,q, которые можно считать упорядоченными согласно условию ![]() , то, как показано в [3],
искомое разбиение X состоит из множеств
, то, как показано в [3],
искомое разбиение X состоит из множеств
![]()
где ![]() , и имеет мало общего с
разбиением (14).
, и имеет мало общего с
разбиением (14).
Замечание
3. Выберем векторы fi,
i=1,..,q единичной длины: ![]() ,
i=1,...,q. Тогда
,
i=1,...,q. Тогда
![]() . (16)
. (16)
Множества (16) являются конусами в Rn , ограниченными гиперплоскостями, проходящими через начало
координат. Отсюда следует, что соответствующее приближение ![]() изображения f(×)
инвариантно относительно произвольного преобразования последнего, не
изменяющего его цвет (например
изображения f(×)
инвариантно относительно произвольного преобразования последнего, не
изменяющего его цвет (например ![]() ), в
частности, относительно образования теней на f(×).
), в
частности, относительно образования теней на f(×).
Замечание 4. Для любого
заданного набора попарно различных векторов ![]() оператор
F, приведенный в теореме 2, определяет форму изображения,
принимающего значения
оператор
F, приведенный в теореме 2, определяет форму изображения,
принимающего значения ![]() соответственно на
измеримых множествах
соответственно на
измеримых множествах ![]() (любого) разбиения
X. Всякое такое изображение является
неподвижной (в
(любого) разбиения
X. Всякое такое изображение является
неподвижной (в ![]() ) точкой F:
) точкой F:
![]() , если
, если ![]() , все они изоморфны между
собой. Если некоторые множества из
, все они изоморфны между
собой. Если некоторые множества из ![]() -
пустые, или нулевой меры, соответствующие изображения имеют более простую
форму.
-
пустые, или нулевой меры, соответствующие изображения имеют более простую
форму.
Иначе говоря, в данном случае формой
изображения ![]() является множество всех
изображений, принимающих заданные значения
является множество всех
изображений, принимающих заданные значения ![]() на
множествах положительной меры
на
множествах положительной меры ![]() любого
разбиения X, и их пределов в
любого
разбиения X, и их пределов в ![]() .
.
Теоремы 1 и 2 позволяют
записать необходимые и достаточные условия наилучшего приближения изображения f(×) изображениями
![]() , в котором требуется
определить как векторы
, в котором требуется
определить как векторы ![]() ,
так и множества
,
так и множества ![]() так,
чтобы
так,
чтобы
![]() .
.
Следствие 1.
Пусть Di ,i=1,...,N, - подмножества Rn (15), П - ортогональный проектор (13), ![]() , где
, где ![]() . Тогда
необходимые и достаточные условия
. Тогда
необходимые и достаточные условия ![]() суть следующие:
суть следующие: ![]() , где
, где
![]() ,
, 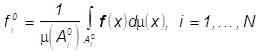 .
.
Следующая рекуррентная процедура, полезная для
уточнения приближений, получаемых в теоремах 1,2, в некоторых случаях позволяет
решать названную задачу. Пусть ![]() - исходные векторы в задаче (14*),
- исходные векторы в задаче (14*), ![]() - соответствующее
оптимальное разбиение (14), F(1)- оператор наилучшего
приближения и
- соответствующее
оптимальное разбиение (14), F(1)- оператор наилучшего
приближения и ![]() - невязка.
Воспользовавшись теоремой 1, определим для найденного разбиения
- невязка.
Воспользовавшись теоремой 1, определим для найденного разбиения ![]() оптимальные векторы
оптимальные векторы ![]() . Согласно выражению
(13)
. Согласно выражению
(13) 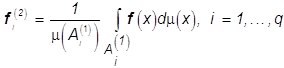 , и соответствующий
оператор наилучшего приближения П(1) (13) обеспечит не менее
точное приближение f(×), чем F(1):
, и соответствующий
оператор наилучшего приближения П(1) (13) обеспечит не менее
точное приближение f(×), чем F(1): ![]() .
Выберем теперь в теореме 2
.
Выберем теперь в теореме 2 ![]() ,
определим соответствующее оптимальное разбиение
,
определим соответствующее оптимальное разбиение ![]() и
построим оператор наилучшего приближения F(2). Тогда
и
построим оператор наилучшего приближения F(2). Тогда ![]() . На следующем шаге по
разбиению
. На следующем шаге по
разбиению ![]() строим
строим ![]() и оператор П(3)
и т.д.
и оператор П(3)
и т.д.
В заключение этого пункта вернемся к
вопросу о построении исчерпывающего ![]() -измеримого
разбиения X, отвечающего заданной функции
-измеримого
разбиения X, отвечающего заданной функции ![]() .
Выберем произвольно попарно различные векторы
.
Выберем произвольно попарно различные векторы ![]() из
f(X) и построим по формуле (15) разбиение Rn
из
f(X) и построим по формуле (15) разбиение Rn ![]() . Для каждого q=1,2,...
образуем разбиение E(N(q)), множества
. Для каждого q=1,2,...
образуем разбиение E(N(q)), множества ![]() , j=1,...,N(q),
которого образованы всеми попарно различными пересечениями
, j=1,...,N(q),
которого образованы всеми попарно различными пересечениями ![]() множеств из
множеств из ![]() . Последовательность
соответствующих разбиений X
. Последовательность
соответствующих разбиений X ![]() , i=1,...,N(q), q=1,2...
, i=1,...,N(q), q=1,2... ![]() -измеримы и
-измеримы и ![]() является продолжением
является продолжением ![]()
5.2. Приближение
изображениями, цвет которых постоянен на подмножествах разбиения ![]() поля
зрения X.
поля
зрения X.
Задано разбиение ![]() , требуется определить цвет
и распределение яркостей наилучшего приближения на каждом Ai,i=1,...,N.
, требуется определить цвет
и распределение яркостей наилучшего приближения на каждом Ai,i=1,...,N.
Для практики, как уже было отмечено, большой интерес представляет класс изображений (5), цвет которых не изменяется в пределах некоторых подмножеств поля зрения, и задачи аппроксимации произвольных изображений изображениями такого класса.
Запишем изображение (5) в виде
![]() (17)
(17)
где ![]() .
.
Пусть A1,...,AN
- заданное разбиение X, ![]() -
индикаторная функция Ai, i=1,...,N. Рассмотрим задачу
наилучшего в
-
индикаторная функция Ai, i=1,...,N. Рассмотрим задачу
наилучшего в ![]() приближения изображения
приближения изображения ![]() изображениями (17), не
требуя, чтобы
изображениями (17), не
требуя, чтобы ![]()
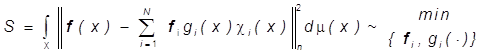 (18)
(18)
Речь идет о задаче аппроксимации
произвольного изображения ![]() изображениями,
у которых яркость может быть произвольной функцией из
изображениями,
у которых яркость может быть произвольной функцией из ![]() , в то время, как цвет
должен сохранять постоянное значение на каждом из заданных подмножеств A1,...,AN
поля
зрения X, (см. Лемму 3).
, в то время, как цвет
должен сохранять постоянное значение на каждом из заданных подмножеств A1,...,AN
поля
зрения X, (см. Лемму 3).
Так как
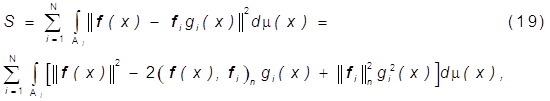
то минимум S (19) по ![]() достигается при
достигается при
![]() , (20)
, (20)
и равен
![]() (21)
(21)
Задача (18) тем самым сведена к задаче
![]() . (22)
. (22)
В связи с последней рассмотрим
самосопряженный неотрицательно определенный оператор ![]()
![]() . (23)
. (23)
Максимум (неотрицательной)
квадратичной формы ![]() на сфере
на сфере ![]() в Rn, как известно, (см.,например, [11]) достигается на собственном
векторе yi оператора Фi,
отвечающем максимальному собственному значению
в Rn, как известно, (см.,например, [11]) достигается на собственном
векторе yi оператора Фi,
отвечающем максимальному собственному значению ![]() >0,
>0,
![]() ,
,
и равен ![]() ,
т.е.
,
т.е. ![]() . Следовательно, максимум в
(22) равен
. Следовательно, максимум в
(22) равен ![]() и достигается, например, при
и достигается, например, при
![]()
Теорема 3. Пусть A1,...,AN -заданное измеримое разбиение X, причем[9]
m(Ai)>0, i=1,...,N. Решением задачи (18) наилучшего
приближения изображения ![]()
![]() изображениями
g(×)
изображениями
g(×)![]() (17) является
изображение
(17) является
изображение
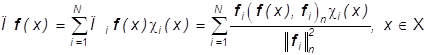 (24)
(24)
Операторы ![]() ,i=1,...,N, и
,i=1,...,N, и ![]() - нелинейные (зависящие от f(×)
- нелинейные (зависящие от f(×)![]() ) проекторы: Пi
проецирует в Rn векторы
) проекторы: Пi
проецирует в Rn векторы ![]()
![]() на линейное подпространство
на линейное подпространство ![]() ,
натянутое на собственный вектор
,
натянутое на собственный вектор ![]() оператора
Фi (23), отвечающий наибольшему собственному
значению ri,
оператора
Фi (23), отвечающий наибольшему собственному
значению ri,
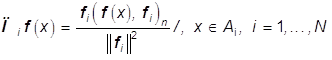 ; (25)
; (25)
П проецирует в ![]() изображение
изображение ![]()
![]() на минимальное линейное
подпространство
на минимальное линейное
подпространство ![]() , содержащее все
изображения
, содержащее все
изображения ![]()
Невязка наилучшего приближения
![]() (19*).
(19*).
Доказательство. Равентство (24) и выражение для Пi следует из (17),(20) и решения задачи на собственные значения для оператора Фi (23). Поскольку Фi самосопряженный неотрицательно определенный оператор, то задача на собственные значения (23) разрешима, все собственные значения Фi неотрицательны и среди них ri - наибольшее.
Для доказательства свойств операторов Пi, i=1,...,N, и П введем обозначения, указывающие на зависимость от f(×):
![]()
![]() (26*)
(26*)
Эти равенства, показывающие, что результат двукратного действия операторов Пi, i=1,...,N, и П (26) не отличается от результатата однократного их действия, позволят считать операторы (26) проекторами.
Пусть fi
- cсобственный вектор Фi , отвечающий
максимальному собственному значению ri. Чтобы определить ![]() следует
решить задачу на собственные значения для оператора
следует
решить задачу на собственные значения для оператора ![]() :
:
![]() .
.
Поскольку rank![]() =1,
=1,
![]() имеет единственное
положительное собственное значение, которое, как нетрудно проверить, равно ri, и ему соответствует единственный собственный вектор fi.
Поэтому
имеет единственное
положительное собственное значение, которое, как нетрудно проверить, равно ri, и ему соответствует единственный собственный вектор fi.
Поэтому
![]() .
.
Отсюда, в свою очередь, следует равенство (26*)
для ![]() n
n
Лемма 4. Для любого
изображения ![]() решение (24)
задачи (18) наилучшего приближения единственно и является элементом
решение (24)
задачи (18) наилучшего приближения единственно и является элементом ![]() .
.
Доказательство. Достаточно доказать,
что единственный (с точностью до положительного множителя) собственный вектор fi
оператора (23), отвечающий максимальному собственному значению ri,
можно выбрать так, чтобы ![]() , поскольку в таком случае будут выполнены импликации:
, поскольку в таком случае будут выполнены импликации:
![]() ,
,
составляющие содержание леммы. Действительно,
если ![]() то согласно (23)
то согласно (23) ![]() , поскольку включение
, поскольку включение ![]() означает, что
означает, что![]()
![]() ; отсюда и из (25) получим,
что
; отсюда и из (25) получим,
что ![]()
![]() ,i=1,...,N, а поэтому
и в (24)
,i=1,...,N, а поэтому
и в (24) ![]()
![]() .
.
Убедимся в неотрицательности ![]() . В ортонормированном базисе
e1,...,en, в котором
. В ортонормированном базисе
e1,...,en, в котором ![]() ,
выходной сигнал i-го детектора в точке
,
выходной сигнал i-го детектора в точке ![]() (см.
замечание 1) задача на собственные значения (23*) имеет вид
(см.
замечание 1) задача на собственные значения (23*) имеет вид ![]() , p=1,...,n,
, p=1,...,n,
где ![]() ,
, ![]() .
.
Так как матрица ![]() симметрическая и
неотрицательно определенная (
симметрическая и
неотрицательно определенная (![]() ) она
имеет n неотрицательных собственных значений
) она
имеет n неотрицательных собственных значений![]() ,
которым соответствуют n ортонормированных собственных векторов
,
которым соответствуют n ортонормированных собственных векторов ![]() , а поскольку матричные
элементы
, а поскольку матричные
элементы ![]() , то согласно теореме
Фробенуса-Перрона максимальное собственное значение
, то согласно теореме
Фробенуса-Перрона максимальное собственное значение ![]() -
алгебраически простое (некратное), а соответствующий собственный вектор можно
выбирать неотрицательным:
-
алгебраически простое (некратное), а соответствующий собственный вектор можно
выбирать неотрицательным:
![]() . Следовательно, вектор fi определен
с точностью до положительного множителя
. Следовательно, вектор fi определен
с точностью до положительного множителя ![]() ,
,
![]() . n
. n
Замечание 4.
Если ![]() , т.е. если
аппроксимируемое изображение на множествах того же разбиения
, т.е. если
аппроксимируемое изображение на множествах того же разбиения ![]() имеет постоянный цвет, то в
теореме 3
имеет постоянный цвет, то в
теореме 3 ![]() ,
, 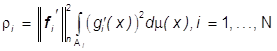 .
.
Наоборот, если ![]() ,
то
,
то
![]() , т.е.
, т.е. ![]() определяется выражением
(17), в котором
определяется выражением
(17), в котором ![]() .
.
Итак, пусть в изображении g(×) (17) все векторы
f1,.…..,fN попарно не коллинеарны, тюею цвета
всех подмножеств A1,...,AN попарно различны. Тогда форма в широком смысле ![]() изображения (17) есть
множество решений уравнения
изображения (17) есть
множество решений уравнения
![]() ,
,![]() , (27)
, (27)
где ![]() , fi - собственный
вектор оператора Фi:
, fi - собственный
вектор оператора Фi: ![]() ,
отвечающий максимальному собственному значению ri,
i=1,...,N . В данном случае
,
отвечающий максимальному собственному значению ri,
i=1,...,N . В данном случае ![]() , если и только если
выполнено равенство (27).
, если и только если
выполнено равенство (27).
Оператор П (24), дающий решение задачи
наилучшего приближения ![]() ,
естественно отождествить с формой в широком смысле изображения
,
естественно отождествить с формой в широком смысле изображения ![]() (17).
(17).
Заданы векторы цвета j1,..., jq, требуется определить разбиение A1,...,
Aq, на множествах которого наилучшее приближение имеет
соответственно цвета j1,..., jq и оптимальные распределения яркостей ![]() [10].
[10].
Речь идет о следующей задаче наилучшего в ![]() приближения
изображения
приближения
изображения ![]()
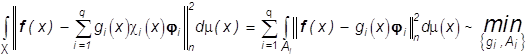 . (28)
. (28)
Рассмотрим вначале задачу (28) не
требуя, чтобы ![]() . Так как для
любого измеримого
. Так как для
любого измеримого ![]()
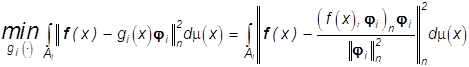 , (29)
, (29)
и достигается на
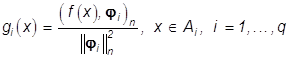 , (30)
, (30)
то, как нетрудно убедиться,
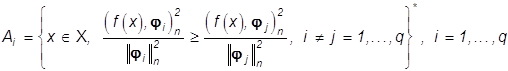 , (31)
, (31)
где звездочка * означает то же самое, что и в
равенстве (14): точки xÎX, в которых
выполняется равенство 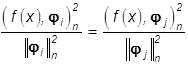 могут
быть произвольно отнесены к одному из множеств Ai или Aj.
могут
быть произвольно отнесены к одному из множеств Ai или Aj.
Пусть
![]() - разбиение
- разбиение ![]() , в котором
, в котором
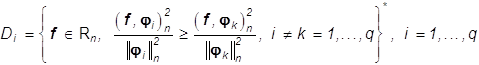 (32)
(32)
а F: Rn-> Rn оператор, определенный условием
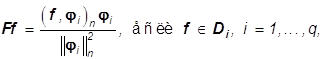 (33)
(33)
Тогда решение задачи (28) можно представить в виде
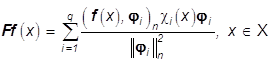 , (34)
, (34)
где ![]() -
индикаторная функция множества Ai (31), i=1,...,q и F
-оператор, действующий в
-
индикаторная функция множества Ai (31), i=1,...,q и F
-оператор, действующий в ![]() по
формуле (34) (см. сноску 4 на стр. 13).
по
формуле (34) (см. сноску 4 на стр. 13).
Нетрудно убедиться, что задача на
минимум (29) с условием физичности ![]()
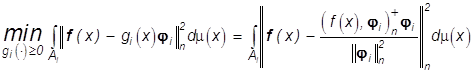 (35)
(35)
имеет решение
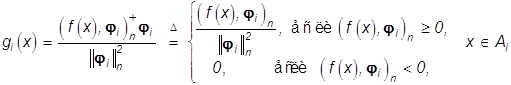 (36)
(36)
Соответственно решение задачи (28) с условием физичности имеет вид
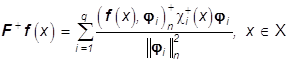 , (37)
, (37)
где ![]() -
индикаторная функция множества
-
индикаторная функция множества
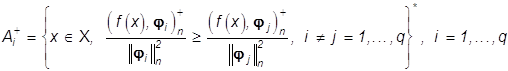 , (38)
, (38)
В ряде случаев для построения (34) полезно определить оператор F+: Rn-> Rn, действующий согласно формуле
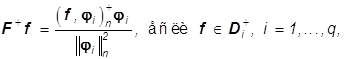 (39)
(39)
где
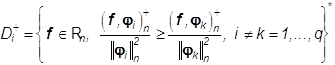 , так что
, так что ![]() ,i=1,...q. (40)
,i=1,...q. (40)
Подытожим сказанное.
Теорема 4. Решение задачи (28)
наилучшего в ![]() приближения
изображения
приближения
изображения ![]() изображениями
на искомых множествах A1,...,Aq разбиения X заданные цветами
j1,..., jq соответственно, дается равенством (34), искомое разбиение A1,...,Aq
определено в (31). Требование физичности
наилучшего приближения приводит к решению (37) и определяет искомое
разбиение формулами (38). Решение (34) инвариантно относительно
любого, а (37) - относительно любого, сохраняющего физичность,
преобразования, неизменяющего его цвет.
изображениями
на искомых множествах A1,...,Aq разбиения X заданные цветами
j1,..., jq соответственно, дается равенством (34), искомое разбиение A1,...,Aq
определено в (31). Требование физичности
наилучшего приближения приводит к решению (37) и определяет искомое
разбиение формулами (38). Решение (34) инвариантно относительно
любого, а (37) - относительно любого, сохраняющего физичность,
преобразования, неизменяющего его цвет.
Формой в широком смысле
изображения, имеющего заданный набор цветов j1,..., jq на некоторых множествах
положительной меры A1,...,Aq разбиение поля зрения можно назвать оператор ![]() (34),
формой такого изображения является оператор F+ (37). Всякое
такое изображение g(×), удовлетворяющее условиям физичности (неотрицательности
яркостей), удовлетворяет уравнению F+g(×)=g(×), те
из них, у которых m(Ai)>0, i=1,...,q, изоморфны, остальные
имеют более простую форму. n
(34),
формой такого изображения является оператор F+ (37). Всякое
такое изображение g(×), удовлетворяющее условиям физичности (неотрицательности
яркостей), удовлетворяет уравнению F+g(×)=g(×), те
из них, у которых m(Ai)>0, i=1,...,q, изоморфны, остальные
имеют более простую форму. n
В заключение этого раздела вернемся
к понятию формы изображения, заданного с точностью до произвольного,
удовлетворяющего условиям физичности, преобразования яркости. Речь идет о форме
изображения ![]() , заданного распределением
цвета
, заданного распределением
цвета ![]() , при произвольном
(физичном) распределении яркости, например,
, при произвольном
(физичном) распределении яркости, например, ![]() .
Для определения формы
.
Для определения формы ![]() рассмотрим задачу
наилучшего в
рассмотрим задачу
наилучшего в ![]() приближения изображения
приближения изображения ![]() такими изображениями
такими изображениями
![]() , (41)
, (41)
Теорема 5. Решение ![]() задачи (41) дается
равенством
задачи (41) дается
равенством
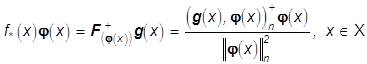 , (42)
, (42)
в котором 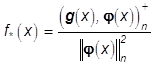 , где
, где
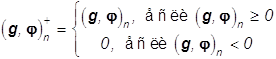 . Невязка приближения
. Невязка приближения
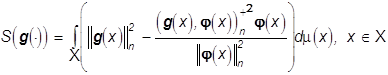 , (43)
, (43)
( ![]() !) n
!) n
Определение. Формой
изображения, заданного распределением цвета ![]() ,
назовем выпуклый, замкнутый конус изображений
,
назовем выпуклый, замкнутый конус изображений
![]()
или - проектор ![]() на
на
![]() .
.
Всякое изображение g(×),
распределение цвета которого есть j(×) и только такое изображение содержится
в ![]() и является неподвижной
точкой оператора
и является неподвижной
точкой оператора
![]() :
: ![]() g(×) = g(×). (#)
g(×) = g(×). (#)
Поскольку на самом деле детали
сцены, передаваемые распределением цвета j(×), не
представлены на изображении f(×) = f(×)j(×) в той
области поля зрения, в которой яркость f(x)=0, xÎX, будем считать, что ![]() - форма любого изображения f(x)
= f(x)j(x), f(x)>0, xÎX(modm), все такие
изображения изоморфны, а форма всякого изображения g(×),
удовлетворяющего уравнению (#), не сложнее, чем форма f(×).
- форма любого изображения f(x)
= f(x)j(x), f(x)>0, xÎX(modm), все такие
изображения изоморфны, а форма всякого изображения g(×),
удовлетворяющего уравнению (#), не сложнее, чем форма f(×).
Замечание 5. Пусть j1,..., jN![]() - исходный набор цветов,
- исходный набор цветов, ![]() , A1,...,AN
- соответствующее оптимальное разбиение X, найденное в теореие 4 и
, A1,...,AN
- соответствующее оптимальное разбиение X, найденное в теореие 4 и
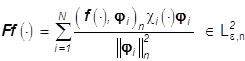 , (34*)
, (34*)
- наилучшее приближение f(×). Тогда в равенстве (24)
если A1,...,AN -
исходное разбиение X в теореме 3. Наоборот, если A1,...,AN -
заданное в теореме 3 разбиение X
и f1,...,fN -
собственные векторы операторов Ф1,...,ФN (23)
соответственно, отвечающие максимальным собственным значениям, то f1,...,fN
![]() и будет выполнено равенство
(24), если в (34*) определить ji как цвет fi в (24), i=1,...,N.
и будет выполнено равенство
(24), если в (34*) определить ji как цвет fi в (24), i=1,...,N.
Проверка этого замечания не представляет затруднений.
В. Случай, когда допускаются небольшие изменения цвета в пределах каждого Ai, i=1,...,N.
Разумеется, условие постоянства
цвета на множествах Ai, i=1,...,N, на практике может выполняться лишь с определенной точностью.
Последнюю можно повысить как путем перехода к более мелкому разбиению ![]() , так и допустив некоторые изменения цвета в пределах каждого Ai, i=1,...,N, например, выбрав вместо
(17) класс изображений
, так и допустив некоторые изменения цвета в пределах каждого Ai, i=1,...,N, например, выбрав вместо
(17) класс изображений
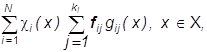 (17*)
(17*)
в котором ![]() в
(3).
в
(3).
Поскольку в задаче наилучшего
приближения f(×)
изображениями этого класса предстоит найти 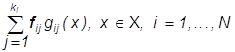 ,
векторы
,
векторы ![]() при любом i=1,...,N,
можно считать ортогональными, определив
при любом i=1,...,N,
можно считать ортогональными, определив
![]() , (*)
, (*)
из условия минимума невязки по ![]() . После этого для каждого i=1,...,N
векторы
. После этого для каждого i=1,...,N
векторы ![]() должны быть определены из
условия
должны быть определены из
условия
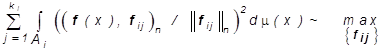 (**)
(**)
при дополнительном условии ортогональности
![]() . Решение этой задачи дается в следующей лемме
. Решение этой задачи дается в следующей лемме
Лемма 5. Пусть ![]() ортогональные собственные
векторы оператора Фi (23), упорядоченные по убыванию
собственных значений:
ортогональные собственные
векторы оператора Фi (23), упорядоченные по убыванию
собственных значений:
![]() .
.
Тогда решение задачи (**) дается равенствами ![]() .
.
Доказательство. Заметим, что,
поскольку Фi - самосопряженный неотрицательно
определенный оператор, его собственные значения неотрицательны, а его
собственные векторы всегда можно выбрать так, чтобы они образовали
ортогональный базис в Rn. Пусть Pi
- ортогонально проецирует в Rn на линейную оболочку ![]() собственных векторов
собственных векторов ![]() и
и
[Pi Фi Pi]
- сужение оператора Pi Фi Pi на ![]() . Тогда левая часть (*)
равна следу оператора [Pi Фi Pi]
. Тогда левая часть (*)
равна следу оператора [Pi Фi Pi]
![]() , где
, где ![]() - j-ое
собственное значение оператора
- j-ое
собственное значение оператора ![]() (см.,
например, [10]). Пусть
(см.,
например, [10]). Пусть ![]() . Тогда
согласно теореме Пуанкаре, [10],
. Тогда
согласно теореме Пуанкаре, [10], ![]() , откуда
следует утверждаемое в лемме. ■
, откуда
следует утверждаемое в лемме. ■
Воспользовавшись выражениями (*) и леммой 5, найдем, что в рассматриваемом случае имеет место утверждение, аналогичное теореме 3.
Теорема 3*. Наилучшее приближение любого изображения f(×) изображениями (17*) имеет вид
![]() ,
,
Где ![]() :
ортогональный проектор на линейную оболочку
:
ортогональный проектор на линейную оболочку ![]() ,
собственных векторов задачи
,
собственных векторов задачи
![]() .
.
Невязка наилучшего приближения равна
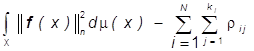 . n
. n
Рассмотрим теперь задачу наилучшего
приближения изображения f(×) изображениями
(17), в которых заданы и фиксированы векторы ![]() ,
и надлежит определить измеримое разбиение
,
и надлежит определить измеримое разбиение ![]() и
функции
и
функции ![]() , как решение задачи
, как решение задачи
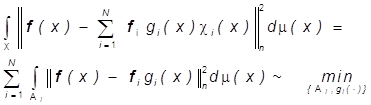 (30)
(30)
При любом разбиении ![]() минимум в (30) по
минимум в (30) по ![]() достигается при
достигается при ![]() , определяемых равенством
(20). В свою очередь, очевидно, что
, определяемых равенством
(20). В свою очередь, очевидно, что
![]() (31)
(31)
где точки ![]() ,
в которых выполняется равенство
,
в которых выполняется равенство ![]() могут
быть произвольно включены в одно из множеств : либо в
могут
быть произвольно включены в одно из множеств : либо в ![]() , либо в
, либо в ![]() . Это соглашение отмечено
звездочкой в (31).
. Это соглашение отмечено
звездочкой в (31).
Таким образом доказана
Теорема 6. Пусть ![]() заданные векторы Rn. Решением задачи (30) является
изображение
заданные векторы Rn. Решением задачи (30) является
изображение
![]() ,
,
где ортогональный проектор ![]() определен равенством
(25), а
определен равенством
(25), а ![]() - индикаторная
функция множества (31), i=1,...,N. Невязка наилучшего приближения
равна
- индикаторная
функция множества (31), i=1,...,N. Невязка наилучшего приближения
равна
![]() . n
. n
Замечание 5. Так как при ![]()
![]() ,
,
то условия (31), определяющие разбиение ![]() , можно записать в виде
, можно записать в виде
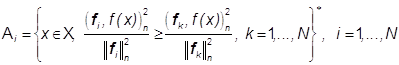 ,
(32)
,
(32)
показывающем, что множество ![]() в (32) инвариантно
относительно любого преобразования изображения
в (32) инвариантно
относительно любого преобразования изображения ![]() ,
не изменяющего его цвет.
,
не изменяющего его цвет.
Теоремы
3 и 6 позволяют сформулировать необходимые и достаточные условия наилучшего
приближения изображения f(×)
изображениями (17), при котором должны быть найдены ![]() и ci0 , i=1,...,N,
такие, что
и ci0 , i=1,...,N,
такие, что
![]() .
.
Теорема 7. Для
заданного изображения f(×) определим множества ![]() равенствами (32), оператор
П - равенством (24),
равенствами (32), оператор
П - равенством (24), ![]() -
равенствами (25). Тогда
-
равенствами (25). Тогда ![]() ,
,
определено равенством (32), в
котором ![]() - собственный
вектор оператора Фi (23), отвечающий наибольшему собственному значению, причем
в (23)
- собственный
вектор оператора Фi (23), отвечающий наибольшему собственному значению, причем
в (23) ![]() , наконец,
, наконец, ![]() будет
дано равенством (20), в котором
будет
дано равенством (20), в котором ![]() , где
, где ![]() - собственный вектор
оператора
- собственный вектор
оператора ![]() , отвечающий
наибольшему собственному значению
, отвечающий
наибольшему собственному значению ![]() ; наконец,
; наконец,
![]() .
n
.
n
Замечание 6. Следующая
итерационная процедура полезна при отыскании ![]() : Для
изображения f(×)
зададим
: Для
изображения f(×)
зададим ![]() и по теореме 5
найдем
и по теореме 5
найдем ![]() и
и ![]() , затем по теореме 3,
используя
, затем по теореме 3,
используя ![]() найдем
найдем ![]() и
и ![]() . После этого вновь воспользуемся
теоремой 3 и по
. После этого вновь воспользуемся
теоремой 3 и по ![]() найдем
найдем ![]() и
и ![]() и т.д. Построенная таким
образом последовательность изображений
и т.д. Построенная таким
образом последовательность изображений ![]() очевидно
обладает тем свойством, что числовая последовательность
очевидно
обладает тем свойством, что числовая последовательность ![]() , k=1,2,.….. монотонно не возрастает и, следовательно, сходится.
К сожалению ничего определенного нельзя сказать о сходимости последовательности
, k=1,2,.….. монотонно не возрастает и, следовательно, сходится.
К сожалению ничего определенного нельзя сказать о сходимости последовательности
![]() .
.
Формы ![]() (10) и
(10) и ![]() (9) удобно задавать операторами
Пf и
П*f
соответственно.
(9) удобно задавать операторами
Пf и
П*f
соответственно.
Теорема 7. Форма
![]() в
широком смысле изображения
в
широком смысле изображения ![]() определяется
ортогональным проектором П*f :
определяется
ортогональным проектором П*f :
![]() ,
,
при этом 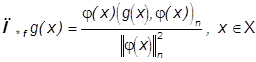 и
и
![]() .
.
Доказательство.
Так как для ![]()
![]() , то получаем первое
утверждение. Для доказательства второго утверждения рассмотрим выпуклую задачу
на минимум
, то получаем первое
утверждение. Для доказательства второго утверждения рассмотрим выпуклую задачу
на минимум ![]() ,
решение которой определяется условиями (см., например, [11])
,
решение которой определяется условиями (см., например, [11])
![]() . Отсюда следует, что
. Отсюда следует, что 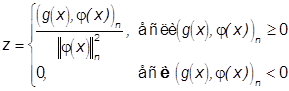 и тем самым доказано и
второе утверждение n
и тем самым доказано и
второе утверждение n
Замечание. Так как ![]() , где fi(x) - выходной
сигнал i-го детектора в точке
, где fi(x) - выходной
сигнал i-го детектора в точке ![]() , причем fi(x)³0 ,i=1,...,n,
и, следовательно цвет
, причем fi(x)³0 ,i=1,...,n,
и, следовательно цвет ![]() реальных
изображений непременно имеет неотрицательные
реальных
изображений непременно имеет неотрицательные ![]() , то для реальных
изображений
, то для реальных
изображений ![]() ,
условия
,
условия ![]() и
и ![]() , эквивалентны. Если же для
некоторого
, эквивалентны. Если же для
некоторого ![]() , то условие
, то условие ![]() не влечет
не влечет ![]() . Заметим также, что для
изображений g(×),
удовлетворяющих условию
. Заметим также, что для
изображений g(×),
удовлетворяющих условию ![]() , всегда
, всегда
![]() .
.
Для спектрозональных изображений характерна ситуация, при которой k детекторов регистрируют рассеянную объектами солнечную радиацию в диапазоне видимого света, а остальные n-k регистрируют собственное тепловое излучение объектов ( в инфракрасном диапазоне). В таком случае любое изображение можно представить разложением
![]() (40)
(40)
В котором
![]() .
Если ИК составляющей солнечного излучения можно пренебречь по сравнению с
собственным излучением объектов, то представляет интерес задача приближения
изображениями f(×) ,
в которых f1(×)
- любая неотрицательная функция из
.
Если ИК составляющей солнечного излучения можно пренебречь по сравнению с
собственным излучением объектов, то представляет интерес задача приближения
изображениями f(×) ,
в которых f1(×)
- любая неотрицательная функция из ![]() ,
j1(×) - фиксированное векторное поле цвета, f2(×) - термояркость, j2(×) -
термоцвет в точке
,
j1(×) - фиксированное векторное поле цвета, f2(×) - термояркость, j2(×) -
термоцвет в точке ![]() . Форма П*f видимой компоненты f(×) (40)
определяется как оператор наилучшего приближения в задаче
. Форма П*f видимой компоненты f(×) (40)
определяется как оператор наилучшего приближения в задаче
![]() ,
в данном случае
,
в данном случае
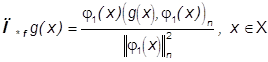 ,
причем П*f
действует фактически только на "видимую
компоненту" g(×), обращая "невидимую, ИК, компоненту" g(×) в
ноль.
,
причем П*f
действует фактически только на "видимую
компоненту" g(×), обращая "невидимую, ИК, компоненту" g(×) в
ноль.
Форма ИК компоненты f(×) может быть определена лишь тогда, когда известно множество возможных преобразований j2(×) f2(×).
Некоторые применения.
Задачи идентификации сцен.
Рассмотрим вначале задачи идентификации сцен по их изображения, неискаженным геометрическими преобразованиями, поворотами, изменениями масштаба и т.д. Ограничимся задачами, в которых предъявляемые для анализа изображения получены при изменяющихся и неконтролируемых условиях освещения и неизвестных и, вообще говоря, различных оптических характеристиках сцены.
1). Задачи идентификации при произвольно меняющейся интенсивности освещения.
Можно ли считать f(×) и g(×) изображениями одной и той же сцены, возможно, отличающимя лишь распределениями яркости, например, наличием теней?
В простейшем случае для
идентификации достаточно воспользоваться теоремой 5, а именно, f(×) и g(×) можно
считать изображениями одной и той же сцены, если существует распределение цвета
![]() , для которого v(j(×))
содержит f(×) и g(×). Если
, для которого v(j(×))
содержит f(×) и g(×). Если ![]() , и
, и ![]() , то, очевидно, существует
, то, очевидно, существует ![]() , при котором f(x)Îv(j(×)), g(x)Îv(j(×)), а
именно,
, при котором f(x)Îv(j(×)), g(x)Îv(j(×)), а
именно, ![]() ,
, ![]() , если
, если ![]() ,
, ![]() , если
, если ![]() , и, наконец,
, и, наконец, ![]() - произвольно, если
- произвольно, если ![]() .
.
На практике удобнее использовать другой подход, позволяющий одновременно решать задачи совмещения изображений и выделения объектов. Можно ли, например, считать g(×) изображением сцены, представленной изображением f(×)? Ответ следует считать утвердительным, если
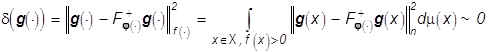 .
.
Здесь j(×) -
распределение цвета на изображении f(×), символ ~0
означает, что значение d(g(×)) можно объяснить наличием шума, каких-либо других погрешностей,
или, наконец, - наличием или, наоборот, отсутствием объектов объясняющим
несовпадение g(×) и f(×) с точностью до преобразования распределения яркостей. Такие
объекты, изменившие распределение цвета g(×) по
сравнению с распределением цвета f(×), представлены в ![]() .
.
2).Идентификация при произвольном изменении распределения интенсивности и пространственно однородном изменении спектрального состава освещения.
Можно ли считать изображением сцены, представленной на изображении f(×), изображение, полученное при изменившихся условиях регистрации, например, перемещением или изменением теней и изменением спектрального состава освещения?
Пусть П - форма в широком
смысле изображения f(×), определенная в теореме @, П*
- форма f(×). Тогда ответ на поставленный вопрос можно считать утвердительным,
если ![]() . Если изменение g(×)
обусловлено не только изменившимися условиями регистрации, но также появлением
и (или) исчезновением некоторых объектов, то изменения, обусловленные этим
последним обстоятельством будут представлены на
. Если изменение g(×)
обусловлено не только изменившимися условиями регистрации, но также появлением
и (или) исчезновением некоторых объектов, то изменения, обусловленные этим
последним обстоятельством будут представлены на ![]() .
.
3). Задачи совмещения изображений и поиска фрагмента.
Пусть f(×) - заданное изображение, AÌX - подмножество поля зрения, cA(×) - его индикатор, cA(×)f(×) -назовем фрагментом изображения f(×) на подмножестве A, представляющем выделенный фрагмент сцены, изображенной на f(×). Пусть g(×) - изображение той же сцены, полученное при других условиях, в частности, например, сдвинутое, повернутое, т.е. геометрически искаженное по сравнению с f(×). Задача состоит в том, чтобы указать на g(×) фрагмент изображения, представляющий на f(×) фрагмент сцены и совместить его с cA(×)f(×).
Ограничимся случаем, когда
упомянутые геометрические искажения можно моделировать группой преобразований R2->R2, преобразование изображения ![]() назовем сдвигом g(×) на h.
Здесь
назовем сдвигом g(×) на h.
Здесь
Q(h): Rn->Rn, hÎH, - группа операторов. Векторный сдвиг на h¢ÎH даст
![]() .
.
В задаче выделения и совмещения фрагмента рассмотрим фрагмент сдвинутого на h изображения g(×) в “окне” A:
![]() (100)
(100)
причем, поскольку ![]() где
где
![]() то в (100)
то в (100) ![]() - ограничение на сдвиг
“окна” А, которое должно оставаться в пределах поля зрения X.
- ограничение на сдвиг
“окна” А, которое должно оставаться в пределах поля зрения X.
Если кроме цвета g(×) может
отличаться от f(×), скажем, произвольным преобразованием распределения яркости при
неизменном распределении цвета и ![]() - форма
фрагмента f(×), то задача выделения и совмещения фрагмента сводится к следующей
задаче на минимум
- форма
фрагмента f(×), то задача выделения и совмещения фрагмента сводится к следующей
задаче на минимум
![]() .(101)
.(101)
При этом считается, что фрагмент изображения g(×), соответствующий фрагменту cA(×)f(×), будет помещен в “окно”.А путем соответствующего сдвига h=h*, совпадает с cA(×)f(×) с точностью до некоторого преобразования распределения яркости на нем. Это означает, что
![]() .
.
т.е. в (101) при h=h* достигается минимум.
4). В ряде случаев возникает следующая задача анализа спектрозональных изображений: выделить объекты которые “видны”, скажем, в первом канале и “не видны” в остальных.
Рассмотрим два изображения ![]() и
и ![]() . Определим форму в широком
смысле
. Определим форму в широком
смысле ![]() как множество всех линейных
преобразований
как множество всех линейных
преобразований ![]() :
: ![]() (A - линейный
оператор R2->R2, не зависящий от xÎX). Для определения проектора на
(A - линейный
оператор R2->R2, не зависящий от xÎX). Для определения проектора на ![]() рассмотрим
задачу на минимум
рассмотрим
задачу на минимум
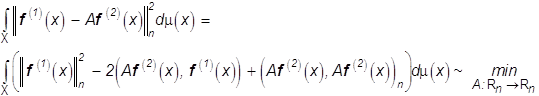 . [*]
. [*]
Пусть ![]() ,
, ![]() , тогда задача на минимум
[*] эквивалентна следующей: tr A*AS - 2trAB ~
, тогда задача на минимум
[*] эквивалентна следующей: tr A*AS - 2trAB ~ ![]() . Ее решение
. Ее решение ![]() (знаком - обозначено
псевдообращение).
(знаком - обозначено
псевдообращение).
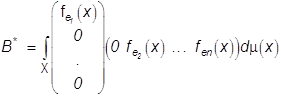 =
=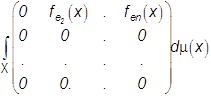
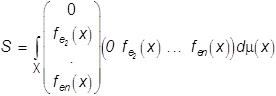 =
=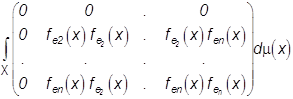
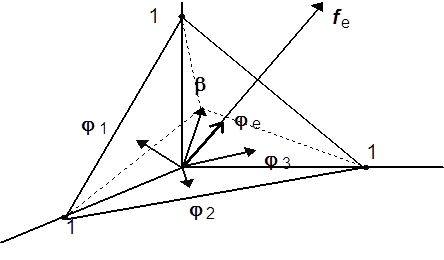
Рис.1.
fe - вектор выходных сигналов детекторов, отвечающий излучению e(×), je - его цвет; j1,j2,j3, - векторы (цвета) базовых излучений, b - белый цвет, конец вектора b находится на пересечении биссектрис.
Литература.
[1] Пытьев Ю.П. Морфологические понятия в задачах анализа изображений, - Докл. АН СССР, 1975, т. 224, №6, сс. 1283-1286.
[2] Пытьев Ю.П. Морфологический анализ изображений, - Докл. АН СССР, 1983, т. 296, №5, сс. 1061-1064.
[3] Пытьев Ю.П. Задачи морфологического анализа изображений, - Математические методы исследования природных ресурсов земли из космоса, ред. Золотухин В.Г., Наука, Москва, 1984, сс. хххх-ххххх.
[4] Пытьев Ю.П., Чуличков А.И. ЭВМ анализирует форму изображения, - Знание,сер. Математика, Кибернентика, Москва, 1988, 47 стр.
[5] Yu.P.Pyt’ev. Morphological Image Analysis, Patt. Recogn. and Image Analysis, 1993, v.3, #1, pp.19-28.
[6] Антонюк В.А., Пытьев Ю.П. Спецпроцессоры реального времени для морфологического анализа реальных сцен. Обработка изображений и дистанционное исследования, -Новосибирск, 1981, сс. 87-89.
[7] Антонюк В.А., Пытьев Ю.П., Рау Э.И. Автоматизация визуального контроля изделий микроэлектроники,Радиотехника и электроника, 1985, т. ХХХ,№12, сс. 2456-2458.
[8] Ермолаев А.Г., Пытьев Ю.П. Априорные оценки полезного сигнала для морфологических решающих алглритмов, - Автоматизация, 1984, №5, сс. 118-120.
[9] Пытьев Ю.П, Задорожный С.С., Лукьянов А.Е. Об автоматизации сравнительного морфологического анализа электронномикроскопических изображений, - Изв. АН СССР, сер. физическая, 1977, т. 41, №11, сс. хххх-хххх.
[10] A.A. Stepanov, S.Yu. Zheltov, Yu.V. Visilter. Shape analysis using Pyt'ev morphological paradigm and its using in machine vision. Proc. SPIE - Th. Intern. Soc. For Optical Engineering Videometrics III, 1994, v. 2350, pp. 163-167.
[11] Пытьев Ю.П.. Математические методы интерпретации эксперимента, Высшая школа, 351 стр., 1989.
[12] Майзель С.О. Ратхер Е.С. Цветовые расчеты и измерения. М:Л:Госэнергоиздат 1941, (Труды всесоюзного электротехнического института, вып.56).
[13] P. Kronberg. Fernerkundung der Erde Ferdinand Enke. Verlag Stuthgart 1985.
[1] Например, в связи с изменением времени суток, погоды, времени года и т.п.
[2] Фрагмент морфологического анализа цветных изображений содержится в работе[3].
[3] вектор fe будет иметь отрицательные координаты, если он не принадлежит выпуклому конусу
[4]черта символизирует замыкание, - выпуклый замкнутый конус в Rn.
[5] Если - более детальное изображение , то некоторые A(j) могут “ращепиться” на несколько подмножеств A¢(j¢), на каждом из которых цвет постоянный, но различный на разных подмножествах A¢(j¢). Однако, поскольку форма обычно строится исходя из данного изображения f(×), v(f(×)) не может содержать изображения, которые более детально характеризуют изображенную сцену.
[6] Для простоты яркость изображения считается положительной в каждой точке поля зрения Х.
[7]- класс неотрицательных функций принадлежащих .
[8]Одна и та же буква F использована как для оператора , так и для оператора . Эта вольность не должна вызывать недоразумения и часто используется в работе.
[9]Если m(As)=0, то в задаче наилучшего приближения (18) цвет и распределение яркости на As можно считать произвольными, поскольку их значения не влияют на величину невязки s.
[10]Векторы j1,..., jq выбираются, например, сообразно цветам объектов, представляющих интерес.
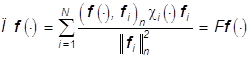 , (24*)
, (24*)