Реферат: Метод касательных (метод Ньютона)

Содержание

Содержание. 1

Используемая литература. 1

Метод Ньютона (касательных). 2

Описание. 2

Блок-схема алгоритма. 3

Листинг программы.. 4

Результаты работы программы.. 6

Пример №1. 6

Пример №2. 6

Пример №3. 7

Метод итераций. 8

Блок-схема алгоритма. 8

Листинг программы.. 9

Результаты работы программы.. 11

Пример №1. 11

Пример №2. 11

Пример №3. 12

Используемая литература

1. http://www.kyshtym.net.ru/rww/ Учимся программировать на С++

2. http://www.sprin.ru/soft.php Решение линейных уравнений методом Ньютона (касательных)

Метод Ньютона (касательных).

Описание

В рамках метода Ньютона предполагается, что функция дифференцируема. Согласно этому методу строится линейная аппроксимация функции в начальной точке, а точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения.

Итерационый процесс схождения к корню реализуется формулой:
xn+1=xn-f(xn)/f '(xn). Вычисления продолжаются пока соблюдается условие
|xn+1-xn |>=eps.

В зависимости от выбора начальной точки и вида функции алгоритм по методу Ньютона может как сходиться к корню уравнения, так и расходиться.

Ниже приведена блок-схема алгоритма и листинг программы, реализующей данный алгоритм на языке С++. Также привожу текст, которая выдает данная программа при решении исходного уравнения.

Блок-схема алгоритма

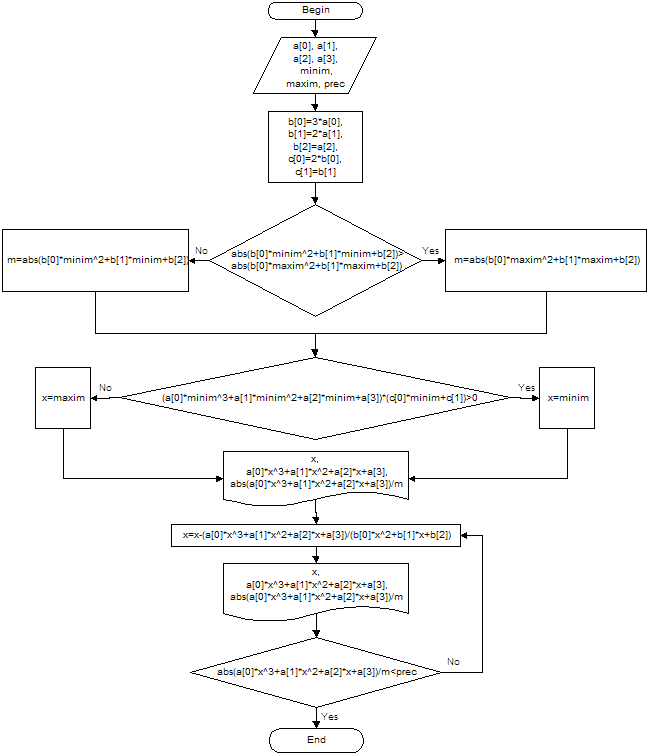
Листинг программы

//метод Ньютона для решения кубических уравнений

#include<math.h>

#include<iostream.h>

double a[4]={0},

b[3]={0},

c[2]={0},

prec=0.00000;

double minim=0, maxim=0;

void Hello(void);

void Input();

void Derivative();

void Calculation();

double Calc_Fun(double);

double Calc_First(double);

double Calc_Second(double);

main(void)

{

Hello();

Input();

Derivative();

Calculation();

return 0;

}

void Hello(void)

{

cout<<"Программа для решения кубических уравнений методом касательных (метод Ньютона).\n\n";

}

void Input()

{

cout<<"Кубическое уравнение имеет вид"<<endl

<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;

for (int i=0;i<4;i++)

{

cout<<"Введите значение коэффициента a["<<i+1<<"] : ";

cin>>a[i];

}

cout<<endl<<"Необходимо указать интервал поиска решения."<<endl

<<"Введите нижнюю границу поиска : ";

cin>>minim;

cout<<"Введите верхнюю границу поиска : ";

cin>>maxim;

while(minim==maxim||minim>maxim)

{

cout<<"\nНижняя граница должна быть меньше верхней и не может быть ей равна."<<endl

<<"Повторите ввод нижней границы : ";

cin>>minim;

cout<<"Повторите ввод верхней границы : ";

cin>>maxim;

}

cout<<"Введите допустимую погрешность : ";

cin>>prec;

}

void Derivative()

{

b[0]=a[0]*3;

b[1]=a[1]*2;

b[2]=a[2];

c[0]=b[0]*2;

c[1]=b[1];

cout<<"\n\n\n"

<<"Исходное уравнение имеет вид : \n\n"

<<a[0]<<"x^3+("<<a[1]<<")x^2+("<<a[2]<<")x+("<<a[3]<<")=0\n\n"

<<"Первая производная имеет вид : \n\n"

<<"f'(x)="<<b[0]<<"x^2+("<<b[1]<<")x+("<<b[2]<<")\n\n"

<<"Вторая производная имеет вид : \n\n"

<<"f''(x)="<<c[0]<<"x+("<<c[1]<<")\n\n";

}

void Calculation()

if (abs(Calc_Fun(minim))*abs(Calc_Second(minim))>0) x=minim;

double Calc_Fun(double x)

{

return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);

}

double Calc_First(double x)

{

return (b[0]*x*x+b[1]*x+b[2]);

}

double Calc_Second(double x)

{

return (c[0]*x+c[1]);

}

Результаты работы программы

Пример №1

Программа для решения кубических уравнений методом касательных (метод Ньютона).

Кубическое уравнение имеет вид

a1*x^3+a2*x^2+a3*x+a4=0

Введите значение коэффициента a[1] : 1

Введите значение коэффициента a[2] : -6

Введите значение коэффициента a[3] : -9

Введите значение коэффициента a[4] : 58

Необходимо указать интервал поиска решения.

Введите нижнюю границу поиска : -4

Введите верхнюю границу поиска : -3

Введите допустимую погрешность : 0.00005

Исходное уравнение имеет вид :

1x^3+(-6)x^2+(-9)x+(58)=0

Первая производная имеет вид :

f'(x)=3x^2+(-12)x+(-9)

Вторая производная имеет вид :

f''(x)=6x+(-12)

-------------------------------------------------

| Xn | f(Xn) | |f(Xn)|/m |

-------------------------------------------------

| -4| -66| 1.222222222|

| -3.24137931| -9.922506048| 0.183750112|

| -3.079817529| -0.40621762| 0.007522548518|

| -3.07261683|-0.000789793230|1.462580056e-05|

-------------------------------------------------

Пример №2

Программа для решения кубических уравнений методом касательных (метод Ньютона).

Кубическое уравнение имеет вид

a1*x^3+a2*x^2+a3*x+a4=0

Введите значение коэффициента a[1] : 1

Введите значение коэффициента a[2] : -6

Введите значение коэффициента a[3] : -9

Введите значение коэффициента a[4] : 58

Необходимо указать интервал поиска решения.

Введите нижнюю границу поиска : 3

Введите верхнюю границу поиска : 4

Введите допустимую погрешность : 0.00005

Исходное уравнение имеет вид :

1x^3+(-6)x^2+(-9)x+(58)=0

Первая производная имеет вид :

f'(x)=3x^2+(-12)x+(-9)

Вторая производная имеет вид :

f''(x)=6x+(-12)

-------------------------------------------------

| Xn | f(Xn) | |f(Xn)|/m |

-------------------------------------------------

| 3| 4| 0.4444444444|

| 3.222222222| 0.159122085| 0.01768023167|

| 3.231855174| 0.000341137633|3.790418145e-05|

-------------------------------------------------

Пример №3

Программа для решения кубических уравнений методом касательных (метод Ньютона).

Кубическое уравнение имеет вид

a1*x^3+a2*x^2+a3*x+a4=0

Введите значение коэффициента a[1] : 1

Введите значение коэффициента a[2] : -6

Введите значение коэффициента a[3] : -9

Введите значение коэффициента a[4] : 58

Необходимо указать интервал поиска решения.

Введите нижнюю границу поиска : 5

Введите верхнюю границу поиска : 6

Введите допустимую погрешность : 0.00005

Исходное уравнение имеет вид :

1x^3+(-6)x^2+(-9)x+(58)=0

Первая производная имеет вид :

f'(x)=3x^2+(-12)x+(-9)

Вторая производная имеет вид :

f''(x)=6x+(-12)

-------------------------------------------------

| Xn | f(Xn) | |f(Xn)|/m |

-------------------------------------------------

| 6| 4| 0.6666666667|

| 5.851851852| 0.2601229487| 0.04335382479|

| 5.840787634| 0.001413241032| 0.000235540172|

| 5.840726862|4.255405933e-08|7.092343222e-09|

-------------------------------------------------

Метод итераций.

Блок-схема алгоритма

Блок-схема решения и листинг программы, реализующей этот алгоритм на языке программирования С++.

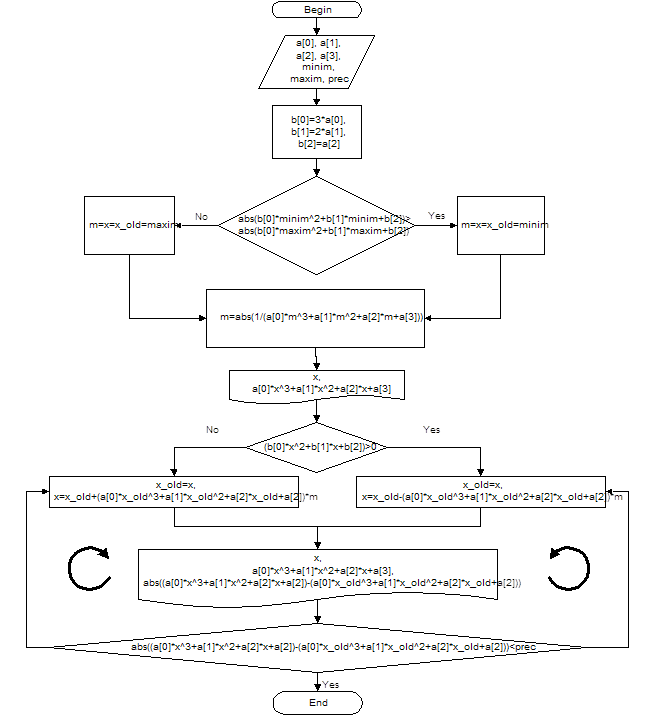
Листинг программы

//метод итераций для решения кубических уравнений

#include<math.h>

#include<iostream.h>

double a[4]={0},

b[3]={0},

prec=0.00000;

double minim=0, maxim=0;

void Hello(void);

void Input();

void Derivative();

void Calculation();

double Calc_Fun(double);

double Calc_First(double);

main(void)

{

Hello();

Input();

Derivative();

Calculation();

return 0;

}

void Hello(void)

{

cout<<"Программа для решения кубических уравнений методом итераций.\n\n";

}

void Input()

{

cout<<"Кубическое уравнение имеет вид"<<endl

<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;

for (int i=0;i<4;i++)

{

cout<<"Введите значение коэффициента a["<<i+1<<"] : ";

cin>>a[i];

}

cout<<endl<<"Необходимо указать интервал поиска решения."<<endl

<<"Введите нижнюю границу поиска : ";

cin>>minim;

cout<<"Введите верхнюю границу поиска : ";

cin>>maxim;

while(minim==maxim||minim>maxim)

{

cout<<"\nНижняя граница должна быть меньше верхней и не может быть ей

равна." <<endl

<<"Повторите ввод нижней границы : ";

cin>>minim;

cout<<"Повторите ввод верхней границы : ";

cin>>maxim;

}

cout<<"Введите допустимую погрешность : ";

cin>>prec;

}

void Derivative()

{

b[0]=a[0]*3;

b[1]=a[1]*2;

b[2]=a[2];

}

void Calculation()

{

double x=0, x_old=0, m=0;

cout<<"-------------------------------------------------"<<endl

<<"| Xn | f(Xn) | X(n+1)-Xn |"<<endl

<<"-------------------------------------------------"<<endl;

if(fabs(Calc_First(minim))>fabs(Calc_First(maxim))) m=x=x_old=minim;

else m=x=x_old=maxim;

m=fabs(1/Calc_First(m));

cout<<"|";

cout.width(15);cout.precision(10);

cout<<x;

cout<<"|";

cout.width(15);cout.precision(10);

cout<<Calc_Fun(x);

cout<<"| |\n";

if(Calc_First(x)>0)

{

while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);

}

else

{

while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);

}

cout<<"-------------------------------------------------";

}

double Calc_Fun(double x)

{

return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);

}

double Calc_First(double x)

{

return (b[0]*x*x+b[1]*x+b[2]);

}

Результаты работы программы

Пример №1

Программа для решения кубических уравнений методом итераций.

Кубическое уравнение имеет вид

a1*x^3+a2*x^2+a3*x+a4=0

Введите значение коэффициента a[1] : 1

Введите значение коэффициента a[2] : -6

Введите значение коэффициента a[3] : -9

Введите значение коэффициента a[4] : 58

Необходимо указать интервал поиска решения.

Введите нижнюю границу поиска : -4

Введите верхнюю границу поиска : -3

Введите допустимую погрешность : 0.00005

-------------------------------------------------

| Xn | f(Xn) | X(n+1)-Xn |

-------------------------------------------------

| -4| -66| |

| -3.24137931| -9.922506048| 56.07749395|

| -3.127327517| -3.12093462| 6.801571427|

| -3.091454705| -1.064778438| 2.056156183|

| -3.079215872| -0.372281515| 0.6924969227|

| -3.074936774| -0.131239433| 0.241042082|

| -3.073428275| -0.04639844126| 0.08484099175|

| -3.07289496| -0.01642029825| 0.02997814301|

| -3.072706221|-0.005813178631| 0.01060711962|

| -3.072639403|-0.002058264249| 0.003754914382|

| -3.072615744|-0.000728799396| 0.001329464852|

| -3.072607367|-0.000258060628|0.0004707387678|

| -3.072604401|-9.137721784e-0|0.0001666834108|

| -3.072603351|-3.235601088e-0|5.902120696e-05|

| -3.072602979|-1.145703711e-0|2.089897377e-05|

-------------------------------------------------

Пример №2

Программа для решения кубических уравнений методом итераций.

Кубическое уравнение имеет вид

a1*x^3+a2*x^2+a3*x+a4=0

Введите значение коэффициента a[1] : 1

Введите значение коэффициента a[2] : -6

Введите значение коэффициента a[3] : -9

Введите значение коэффициента a[4] : 58

Необходимо указать интервал поиска решения.

Введите нижнюю границу поиска : 3

Введите верхнюю границу поиска : 4

Введите допустимую погрешность : 0.00005

-------------------------------------------------

| Xn | f(Xn) | X(n+1)-Xn |

-------------------------------------------------

| 3| 4| |

| 3.222222222| 0.159122085| 3.840877915|

| 3.231062338| 0.01338370012| 0.1457383849|

| 3.231805877| 0.001151957391| 0.01223174272|

| 3.231869875|9.934183961e-05| 0.001052615552|

| 3.231875394|8.568402322e-06|9.077343728e-05|

| 3.23187587|7.390497921e-07| 7.82935253e-06|

-------------------------------------------------

Пример №3

Программа для решения кубических уравнений методом итераций.

Кубическое уравнение имеет вид

a1*x^3+a2*x^2+a3*x+a4=0

Введите значение коэффициента a[1] : 1

Введите значение коэффициента a[2] : -6

Введите значение коэффициента a[3] : -9

Введите значение коэффициента a[4] : 58

Необходимо указать интервал поиска решения.

Введите нижнюю границу поиска : 5

Введите верхнюю границу поиска : 6

Введите допустимую погрешность : 0.00005

-------------------------------------------------

| Xn | f(Xn) | X(n+1)-Xn |

-------------------------------------------------

| 6| 4| |

| 5.851851852| 0.2601229487| 3.739877051|

| 5.842217669| 0.0346921878| 0.2254307609|

| 5.840932773| 0.004788677115| 0.02990351069|

| 5.840755414|0.0006639855431| 0.004124691572|

| 5.840730822|9.212373716e-05|0.0005718618059|

| 5.84072741|1.278267885e-05|7.934105832e-05|

| 5.840726937|1.773688694e-06|1.100899016e-05|

-------------------------------------------------

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ ТАТАРСТАН

АЛЬМЕТЬЕВСКИЙ НЕФТЯНОЙ ИНСТИТУТ

Кафедра информатики

Курсовая работа

На тему: метод касательных (метод Ньютона)

Работу выполнил студент гр. 52-61

Низамова Г.Н.

Проверил: Борганова Э.М.

Альметьевск 2003 г.