╨хЇхЁрЄ√ яю Ёхъырьх
╨хЇхЁрЄ√ яю Їшчшъх
╨хЇхЁрЄ√ яю ЇшыюёюЇшш
╨хЇхЁрЄ√ яю Їшэрэёрь
╨хЇхЁрЄ√ яю їшьшш
╨хЇхЁрЄ√ яю їюч щёЄтхээюьє яЁртє
╨хЇхЁрЄ√ яю ЎшЇЁют√ь єёЄЁющёЄтрь
╨хЇхЁрЄ√ яю ¤ъюыюушўхёъюьє яЁртє
╨хЇхЁрЄ√ яю ¤ъюэюьшъю-ьрЄхьрЄшўхёъюьє ьюфхышЁютрэш■
╨хЇхЁрЄ√ яю ¤ъюэюьшўхёъющ ухюуЁрЇшш
╨хЇхЁрЄ√ яю ¤ъюэюьшўхёъющ ЄхюЁшш
╨хЇхЁрЄ√ яю ¤Єшъх
╨хЇхЁрЄ√ яю ■ЁшёяЁєфхэЎшш
╨хЇхЁрЄ√ яю ч√ъютхфхэш■
╨хЇхЁрЄ√ яю ■Ёшфшўхёъшь эрєърь
╨хЇхЁрЄ√ яю шёЄюЁшш
╨хЇхЁрЄ√ яю ъюья№■ЄхЁэ√ь эрєърь
╨хЇхЁрЄ√ яю ьхфшЎшэёъшь эрєърь
╨хЇхЁрЄ√ яю Їшэрэёют√ь эрєърь
╨хЇхЁрЄ√ яю єяЁртыхэўхёъшь эрєърь
╧ёшїюыюуш ш яхфруюушър
╧Ёюь√°ыхээюёЄ№ яЁюшчтюфёЄтю
┴шюыюуш ш їшьш
▀ч√ъючэрэшх Їшыюыюуш
╚чфрЄхы№ёъюх фхыю ш яюышуЁрЇш
╨хЇхЁрЄ√ яю ъЁрхтхфхэш■ ш ¤ЄэюуЁрЇшш
╨хЇхЁрЄ√ яю Ёхышушш ш ьшЇюыюушш
╨хЇхЁрЄ√ яю ьхфшЎшэх
╨хЇхЁрЄ√ яю ёхъёюыюушш
╨хЇхЁрЄ√ яю шэЇюЁьрЄшъх яЁюуЁрььшЁютрэш■
╩ЁрЄъюх ёюфхЁцрэшх яЁюшчтхфхэшщ
╨хЇхЁрЄ: ╦рсюЁрЄюЁэр ЁрсюЄр яю шэЇюЁьрЄшъх ( ╟рфрўш )
╨хЇхЁрЄ: ╦рсюЁрЄюЁэр ЁрсюЄр яю шэЇюЁьрЄшъх ( ╟рфрўш )
Лабораторная работа 1СИСТЕМЫ СЧИСЛЕНИЯ
ПРАВИЛА ПЕРЕВОДА ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ
Ц е л ь р а б о т ы . Изучение систем счисления, используе-
мых в вычислительной технике и правил перевода чисел из одной
системы счисления в другую.
При использовании ЭВМ существенным является знание систем
счисления. Системы счисления, которыми мы пользуемся в настоящее
время, основаны на методе, открытом индусскими математиками око-
ло 400 г. н.э. Арабы стали пользоваться подобной системой, из-
вестной как арабская система счисления около 800 г.н.э., а при-
мерно в 1200 г.н.э. ее начали применять в Европе и называют де-
сятичной системой счисления.
Известны другие системы счисления, основанные на тех же
принципах, что и десятичная,- двоичная, восьмеричная и шестнад-
цатиричная. Они обычно используются в ЭВМ, поскольку вычисли-
тельные машины построены на схемах с двумя устойчивыми состояни-
ями. В настоящей лабораторной работе предлагается изучить ука-
занные системы счисления, а также методы преобразования чисел из
одной системы счисления в другую.
О п и с а н и е л а б о р а т о р н о й р а б о т ы
Лабораторная работа представлена обучающей программой, ра-
бота с которой осуществляется в интерактивном режиме. (Программа
разработана под руководством доцента кафедры УИТЭС В.М. Дерябина)
Запуск программы осуществляется из директории PEREVOD1,
инициированием файла maindm.exe
Все действия, которые необходимо выполнить в ходе работы
отражаются непосредственно на экране, либо их описания могут
быть получены инициированием меню "Help".
С о д е р ж а н и е о т ч е т а
1.Краткое описание особенностей изученных систем счисления.
2.Результаты преобразования чисел из одной системы счисле-
ния в другую.
К о н т р о л ь н ы е в о п р о с ы
1.Чем отличаются позиционные системы счисления от непозици-
онных?
2.Как можно объяснить правила преобразования двоичной сис-
темы счисления в восьмеричную, шестнадцатиричную, двоично-деся-
тичную и наоборот?
3.В каких случаях преобразование десятичной дроби в двоич-
ную может быть выполнено за конечное число шагов и почему?
4.Переведите:
101101.101 22 4 2 0 в десятичную систему
47 4 10 7 )
0.14 4 10 0 7 8 0 в двоичную систему
24.31 4 10 7 0
5.Переведите:
87.1 4 10 7 )
78 0 в восьмеричную систему;
1011.102 4 2 7 0
124.6 4 8 7 )
78 0 в двоичную систему;
62.42 4 8 0 70
6.Переведите:
BAD.DAD 416 0 в десятичную систему;
374.971 4 10 7 )
78 0 в шестнадцатиричную систему;
1011.101101 4 2 7 0
8AF.CB4 416 0 в восьмеричную систему.
Л и т е р а т у р а
1.Чернов В.Г. Математические и логические основы ЭВМ. Мето-
дические указания к самостоятельной работе студентов.-ВПИ,Влади-
мир 1992-47с.
╦рсюЁрЄюЁэр ЁрсюЄр ╣1.
╓хы№ ЁрсюЄ√: ╚чєўхэшх ьхЄюфют тшчєры№эюую яЁюуЁрььшЁютрэш т Delphi.
╥хъёЄ яЁюуЁрьь√:
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
StdCtrls, ExtCtrls, Buttons;
type
TForm1 = class(TForm)
ScrollBar1: TScrollBar;
ScrollBar2: TScrollBar;
Shape1: TShape;
ColorDialog1: TColorDialog;
Panel1: TPanel;
Button1: TButton;
Button2: TButton;
ComboBox1: TComboBox;
BitBtn1: TBitBtn;
procedure Button2Click(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure ComboBox1Change(Sender: TObject);
procedure ScrollBar1Change(Sender: TObject);
procedure ScrollBar2Change(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.DFM}
procedure TForm1.Button2Click(Sender: TObject);
begin
if ColorDialog1.Execute then
Form1.Color:=ColorDialog1.Color;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
if colorDialog1.Execute then
Shape1.Brush.Color:=ColorDialog1.Color;
end;
procedure TForm1.ComboBox1Change(Sender: TObject);
begin
Shape1.Shape:=TShapeType(ComboBox1.ItemIndex);
end;
procedure TForm1.ScrollBar1Change(Sender: TObject);
begin
Shape1.Width:=ScrollBar1.Position*3;
end;
procedure TForm1.ScrollBar2Change(Sender: TObject);
begin
Shape1.Height:=Scrollbar2.Position*2;
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
begin
Close;
end;
end.
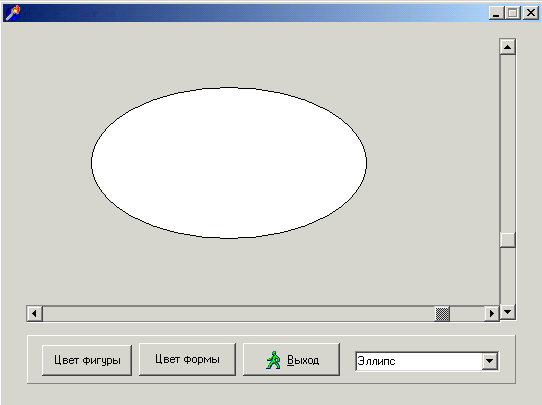
┬эх°эшщ тшф яЁюуЁрьь√: