
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология и педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по информатике программированию
Краткое содержание произведений
Реферат: Двоичные деревья поиска
Реферат: Двоичные деревья поиска
Роман Акопов
Определение Двоичного Дерева Поиска (Binary Search Tree, BST)
Двоичным деревом поиска (ДДП) называют дерево, все вершины которого упорядочены, каждая вершина имеет не более двух потомков (назовём их левым и правым), и все вершины, кроме корня, имеют родителя. Вершины, не имеющие потомков, называются листами. Подразумевается, что каждой вершине соответствует элемент или несколько элементов, имеющие некие ключевые значения, в дальнейшем именуемые просто ключами. Обычно одной вершине соответствует один элемент, поэтому данные термины можно без потери смысла считать синонимами, хотя и надо помнить, что в некоторых реализациях это не так. В приведённых алгоритмах считается, что одной вершине соответствует только один элемент. Поэтому мы будем использовать понятия ключа вершины и данных вершины, подразумевая ключ и данные соответствующего вершине элемента. Мы так же будем понимать под вставкой вершины добавление вершины с указанным значением элемента и присвоение указателям на родителя и потомков корректных значений. Именно ключ используется во всех операциях сравнения элементов. Элемент может также содержать ассоциированные с ключом данные. На практике в качестве ключа может использоваться часть данных элемента. Ключ также может храниться как отдельное значение. ДДП позволяет выполнять следующие основные операции:
Поиск вершины по ключу.
Определение вершин с минимальным и максимальным значением ключа.
Переход к предыдущей или последующей вершине, в порядке, определяемом ключами.
Вставка вершины.
Удаление вершины.
Двоичное дерево может быть логически разбито на уровни. Корень дерева является нулевым уровнем, потомки корня – первым уровнем, их потомки – вторым, и т.д. Глубина дерева это его максимальный уровень. Понятие глубины также может быть описано в терминах пути, то есть глубина дерева есть длина самого длинного пути от корня до листа, если следовать от родительской вершины до потомка. Каждую вершину дерева можно рассматривать как корень поддерева, которое определяется данной вершиной и всеми потомками этой вершины, как прямыми, так и косвенными. Поэтому о дереве можно говорить как о рекурсивной структуре. Эффективность поиска по дереву напрямую связана с его сбалансированностью, то есть с максимальной разницей между глубиной левого и правого поддерева среди всех вершин. Имеется два крайних случая – сбалансированное бинарное дерево (где каждый уровень имеет полный набор вершин) и вырожденное дерево, где на каждый уровень приходится по одной вершине. Вырожденное дерево эквивалентно связанному списку. Время выполнения всех основных операций пропорционально глубине дерева. Таким образом, скоростные характеристики поиска в ДДП могут варьироваться от O(log2N) в случае законченного дерева до O(N) – в случае вырожденного.
ДДП может быть использовано для реализации таких абстракций, как сортированный список, словарь (набор соответствий "ключ-значение"), очередь с приоритетами и так далее.
При реализации дерева помимо значения ключа (key) и данных также хранятся три указателя: на родителя (net), левого (left) и правого (right) потомков. Если родителя или потомка нет, то указатель хранит нулевое (NULL, NIL) значение.
Свойство упорядоченности двоичного дерева поиска
Если x – это произвольная вершина в ДДП, а вершина y находится в левом поддереве вершины x, то y.key <= x.key. Если x – это произвольная вершина ДДП, а вершина y находится в правом поддереве вершины x, то y.key >= x.key. Из свойства следует, что если y.key == x.key, то вершина y может находиться как в левом, так и в правом поддереве относительно вершины x.
Необходимо помнить, что при наличии нескольких вершин с одинаковыми значениями ключа некоторые алгоритмы не будут работать правильно. Например, алгоритм поиска будет всегда возвращать указатель только на одну вершину. Эту проблему можно решить, храня элементы с одинаковыми ключами в одной и той же вершине в виде списка. В таком случае мы будем хранить в одной вершине несколько элементов, но данный случай в статье не рассматривается.
Это двоичное дерево поиска:
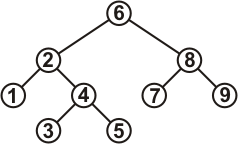
Рисунок 1.
А это нет:
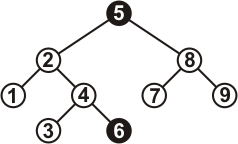
Рисунок 2.
Способы обхода ДДП
Есть три способа обхода: Прямой (preorder), Поперечный (inorder), Обратный (postorder).
Прямой обход: сначала обходится данная вершина, левое поддерево данной вершины, затем правое поддерево данной вершины.
Поперечный обход: сначала обходится левое поддерево данной вершины, затем данная вершина, затем правое поддерево данной вершины. Вершины при этом будут следовать в неубывающем (по ключам key) порядке.
Обратный обход: сначала обходится левое поддерево данной вершины, затем правое, затем данная вершина.
На рисунке 3 порядок обхода вершин указан номерами, при этом предполагается, что сами вершины расположены так, что образуют ДДП.
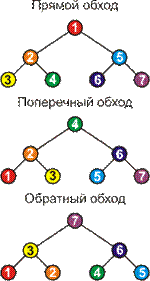
Рисунок 3.
Наиболее часто употребляется поперечный обход, так как во всех других способах обхода следующие друг за другом вершины не связаны никакими условиями отношения.
Поиск вершины в ДДП
Идея поиска проста. Алгоритм поиска в ДДП по своей природе рекурсивен. При его описании проще всего использовать понятие поддерева. Поиск начинается с корня дерева, который принимается за корень текущего поддерева, и его ключ сравнивается с искомым. Если они равны, то, очевидно, поиск закончен. Если ключ, который мы ищем, оказался больше текущего, то, очевидно, что нужная вершина находится в правом поддереве, иначе – в левом. Далее эта операция повторяется для правого или левого поддерева. В условном коде это можно описать так:
Рекурсивно:
|
TreeSearch(node, key) Begin // Если вершина равна NIL, то нечего в ней искать. Так же и возвращаем. // Это нужно для поиска по не существующим потомкам If (node == NIL) Then Return node; // Если нашли, то возвращаем указатель на найденную вершину. If (node.key == key) Then Return node; // Если ключ найденной вершины больше того, который мы ищем If (node.key > key) Then // То искать в левом поддереве Return TreeSearch(node.left, key); Else // Иначе в правом поддереве Return TreeSearch(node.right, key); End |
|
ПРИМЕЧАНИЕ В прилагаемом исходном коде, написанном на паскале-подобном языке, все параметры передаются по значению. nodeParent, nodeTemp и node – это указатели на вершины, а Tree – само дерево, имеющее поле root, указатель на корень дерева. |
Итеративно:
|
TreeSearch(node,key) Begin // Пока ещё есть вершины среди которых можно искать //(мы просматриваем не все, но несколько) и пока мы не нашли While (node != NIL) and (node.key != key) Do Begin // Если ключ найденногй вершины больше того который мы ищем If (node.key > key) Then node = node.left; // То искать в левом поддереве Else node = node.right; // А иначе в правом поддереве End Return node; // Возвратить найденное End |
Поиск вершины с минимальным и максимальным значением ключа
Вершины с минимальным и максимальным значением ключа можно найти, пройдясь по левым (правым) указателям от корня (пока не достигнем NIL). Возвращаемое значение – это указатель на вершину с минимальным (максимальным) значением ключа.
|
TreeMinimum(node) Begin While (node.left != NIL) Do // Пока есть левый потомок Node = node.left; // Перейти к нему Return node; End TreeMaximum(node) Begin While (node.right != NIL) Do // Пока есть правый потомок node = node.right; // Перейти к нему Return node; End |
Нахождение следующей и предыдущей вершины в ДДП
Чтобы найти предыдущую и следующую вершину, надо снова вспомнить свойство упорядоченности. Рассмотрим это на примере функции TreeNext. Она учитывает два случая. Если правое поддерево не пусто, то вершина из правого поддерева с минимальным значением ключа и будет следующей. Если же правое поддерево пусто, тогда мы идём вверх, пока не найдём вершину, являющуюся левым потомком своего родителя. Этот родитель (если он есть) и будет следующей вершиной. Возвращаемое значение – это указатель на вершину с следующим (предыдущим) значеним ключа или NIL, если такой вершины нет.
|
TreeNext(node) Begin // Если правое поддерево не пусто, то возвратить // вершину с минимальным значением ключа из правого поддерева If (node.right != NIL) Then Return TreeMinimum(node.right); nodeParent = node.nodeParent; // Перебирать родителей, пока не найдена вершина, // являющаяся левым потомком своего родителя // или пока не закончатся родители. While (nodeParent != NIL) and (node == nodeParent.right) Do Begin node = nodeParent; nodeParent = nodeParent.nodeParent; End // Возвратить родителя вершины, являющегося левым потомком своего родителя Return nodeParent; End TreePrevious(node) Begin If (node.left != NIL) Then // Если левое поддерево не пусто, то возвратить // вершину из левого поддерева с максимальным значением ключа Return TreeMaximum(node.left); nodeParent = node.nodeParent; // Перебирать родителей, пока не найдём вершину, являющуюся // правым потомком своего родителя или пока не закончатся родители While (nodeParent != NIL) and (node == nodeParent.left) Do Begin node = nodeParent; nodeParent = nodeParent.nodeParent; End // Возвратить родителя вершины являющегося его правым потомком Return nodeParent; End |
Добавление вершины
Добавление вершины в ДДП сопряжено с некоторыми проблемами. После добавления ДДП должно сохранить свойство упорядоченности, а это значит, что вершину, куда попало добавлять нельзя. Поэтому, прежде чем вставлять вершину, необходимо подобрать для неё подходящее место, то есть такое место, после вставки в которое, дерево сохранит своё свойство упорядоченности. Говоря другими словами, нам нужно место после вершины с наибольшим ключом из всех меньших данного.
|
TreeInsert(Tree,node) Begin nodeParent = NIL; nodeTemp = T.root; // Пока ещё есть вершины которые надо просмотреть, то // есть пока мы не добрались до “листочков” дерева While (nodeTemp != NIL) Do Begin nodeParent = nodeTemp; // Если ключ вершины, которую мы хотим вставить, // меньше ключа текущей вершины If (node.key < nodeTemp.key) Then nodeTemp = nodeTemp.left; // То он должен быть в его левом поддереве Else nodeTemp = nodeTemp.right; // А иначе в правом End node.nodeParent = nodeParent; If (nodeParent == NIL) Then // Если в дереве ещё нет вершин Tree.root = node; // То добавить первую Else Begin // Если ключ вершины, которую мы хотим вставить, // меньше ключа вершины, потомком которой должна стать // вставляемая вершина If (node.key < nodeParent.key) Then nodeParent.left = node; // То добавить в дерево как левого потомка Else nodeParent.right = node; // Иначе добавить в дерево как правого потомка End End |
Удаление вершины
Проблемы возникают и при удалении. Нам необходимо сохранить свойство упорядоченности ДДП. При удалении возможны три случая: у удаляемой вершины нет потомков, у удаляемой вершины есть один потомок и у удаляемой вершины два потомка. Если потомков нет, то вершину можно просто удалить. Если потомок один, то удаляемую вершину можно “вырезать”, указав её родителю в качестве потомка единственного имеющегося потомка удаляемой вершины. Если же потомков два, требуются дополнительные действия. Нужно найти следующую за удаляемой (по порядку ключей) вершину, скопировать её содержимое (ключ и данные) в удаляемую вершину (она теперь никуда не удаляется физически, хотя логически исчезает) и удалить найденную вершину (у неё не будет левого потомка). Сначала функция TreeDelete ищет вершину, которую надо удалить, затем переменной nodeTemp присваивается указатель на существующего потомка удаляемой вершины (или NIL, если потомков нет). Далее вершина удаляется из дерева, при этом отдельно рассматриваются случаи: когда потомков нет и когда удаляемая вершина – это корень дерева. Возвращаемое значение – это указатель на удалённую вершину. На неё уже нет никаких ссылок в самом дереве, но она всё ещё занимает память. Момент её реального удаления зависит от используемых методов распределения памяти.
|
TreeDelete(Tree,node) Begin // Если потомков не более одного (случаи 1 и 2) If (node.left == NIL) or (node.right == NIL) Then del = node; // физически удаляем текущую вершину Else del = TreeNext(node); // Иначе следующую If (del.left != NIL) Then // Пытаемся найти хоть одного потомка nodeTemp = del.left; Else nodeTemp = del.right; // Если есть, родителем потомка делаем родителя // удаляемой вершины (случай 2) If (nodeTemp != NIL) Then nodeTemp.nodeParent = del.nodeParent; // Если удаляем корень дерева, надо указать новый корень дерева If (del.nodeParent == NIL) Then Tree.root = nodeTemp; Else Begin // Указываем родителю удаляемой вершины качестве потомка // потомок удаляемой вершины If (del.nodeParent.left == del) Then del.nodeParent.left = nodeTemp; Else del.nodeParent.right = nodeTemp; End If (del != node) Then // Если случай 3 Begin node.key = del.key; // Скопировать ключ { копирование дополнительных данных } End Return del; End |
NIL, NULL и маленькие хитрости
Нередко алгоритмы, просто выглядящие на бумаге, становятся нагромождением сплошных конструкций if в реальной программе. Почему? Ответ очевиден: многие алгоритмы для работы с деревьями предполагают, что (NIL).parent == (NIL).left == (NIL).right == NIL. Вроде всё ясно и даже логично, но ведь во многих языках программирования NIL/NULL – это ноль. А обращение по нулевому адресу памяти чревато нехорошими вещами. Что же делать? Ведь мало того, что все эти if тормозят программу, в них легко запутаться! Решение просто: мы не будем использовать NIL! Действительно, алгоритмам совершенно всё равно, какое численное значение имеет NIL, главное, чтобы адрес любой реальной вершины в дереве не был ему равен. Поэтому вместо NIL мы будем использовать адрес переменной, проинициализированной особым образом. Я покажу это на языке С++, но думаю, этот пример можно будет перевести и на другие языки, хотя там, скорее всего, нет шаблонов, и придется пожертвовать типобезопасностью.
|
template <class CTree>class CTreeBase { protected: CTree * lpCParent; CTree * lpCLeft; CTree * lpCRight; public: CTreeBase(CTreeBase * lpCParentInit, CTreeBase * lpCLeftInit, CTreeBase * lpCRightInit) { lpCParent = (CTree *)lpCParentInit; lpCLeft = (CTree *)lpCLeftInit; lpCRight = (CTree *)lpCRightInit; } }; ///////////////////////////////////// class CTree : public CTreeBase<CTree> { private: int data; protected: static CTreeBase<CTree> treeNil; }; //////////////////////////////////////////////////////////// CTreeBase<CTree> CTree::treeNil(&treeNil, &treeNil, &treeNil); |
Теперь везде в классе CTree можно использовать переменную treeNil. Преимущества очевидны. Потратив каких-то двенадцать (3 * sizeof(CTree *)) байт памяти, мы упростили разработку и ускорили выполнение программы.
Основная проблема использования ДДП
Основной проблемой использования ДДП является то, что методы вставки и удаления вершин, гарантируя сохранение свойства упорядоченности, совершенно не способствуют оптимизации основных операций над ДДП. Например, если вставить в ДДП последовательность возрастающих или убывающих чисел, оно превратится, по сути, в двусвязный список, а основные операции будут занимать время, пропорциональное количеству вершин, а не его логарифму.
Таким образом, для получения производительности порядка O(log2N) нужно, чтобы дерево имело как можно более высокую сбалансированность (то есть имело возможно меньшую высоту). Обычно выделяются несколько типов сбалансированности. Полная сбалансированность, это когда для каждой вершины дерева количества вершин в левом и правом поддеревьях различаются не более чем на 1. К сожалению, такой сбалансированности трудно добиться на практике. Поэтому на практике используются менее жесткие виды сбалансированности. Например, русскими математиками Г. М. Адельсон-Вельским и Е.М.Ландисом были разработаны принципы АВЛ деревьев. В АВЛ деревьях для каждой вершины дерева глубины обоих поддеревьев различаются не более чем на 1. Еще одним “продвинутым” видом деревьев является так называемые красно-чёрные деревья. АВЛ деревья обеспечивают более высокую сбалансированность дерева, но затраты на их поддержание выше. Поскольку на практике разница в сбалансированности между этими двумя видами деревьев не высока, чаще используются красно-чёрные деревья.
Красно-чёрные деревья (Red-Black Tree, RB-Tree)
Итак, одним из способов решения основной проблемы использования ДДП являются красно-чёрные деревья. Красно-чёрные (название исторически связано с игральными картами, поскольку из них легко делать простые модели) деревья (КЧД) – это ДДП, каждая вершина которых хранит ещё одно дополнительное логическое поле (color), обозначающее цвет: красный или чёрный. Фактически, в КЧД гарантируется, что уровни любых двух листьев отличаются не более, чем в два раза. Этого условия оказывается достаточно, чтобы обеспечить скоростные характеристики поиска, близкие к O(log2N). При вставке/замене производятся дополнительные действия по балансировке дерева, которые не могут не замедлить работу с деревом. При описании алгоритмов мы будем считать, что NIL – это указатель на фиктивную вершину, и операции (NIL).left, (NIL).right, (NIL).color имеют смысл. Мы также будем полагать, что каждая вершина имеет двух потомков, и лишь NIL не имеет потомков. Таким образом, каждая вершина становится внутренней (имеющей потомков, пусть и фиктивных), а листьями будут лишь фиктивные вершины NIL.
Свойства КЧД
Каждая вершина может быть либо красной, либо чёрной. Бесцветных вершин, или вершин другого цвета быть не может.
Каждый лист (NIL) имеет чёрный цвет.
Если вершина красная, то оба её потомка – чёрные.
Все пути от корня к листьям содержат одинаковое число чёрных вершин.
Пример КЧД с учётом наших положений приведен на рисунке 4. Учтите, что вершина 9 могла быть и красной, но в дальнейшем мы будем рассматривать только те деревья, у которых корень чёрный. Мы это сделаем для того, чтобы потомки корня могли иметь любой цвет.
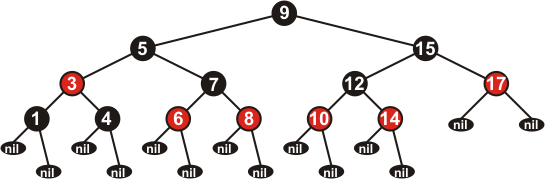
Рисунок 4.
Вращения
Операции вставки и удаления вершин в КЧД могут нарушать свойства КЧД. Чтобы восстановить эти свойства, надо будет перекрашивать некоторые вершины и менять структуру дерева. Для изменения структуры используются операции, называемые вращением. Возвращая КЧД его свойства, вращения так же восстанавливают сбалансированность дерева. Вращения бывают левые и правые, их суть показана на рисунке 5.
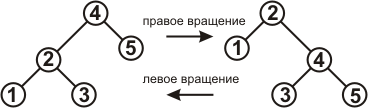
Рисунок 5.
Как видно, вращения, перемещая вершины, не нарушают свойства упорядоченности.
В процедуре RBTLeftRotate предполагается, что node.right != NIL. В процедуре RBTRightRotate предполагается, что node.left != NIL.
|
RBTLeftRotate(Tree,node) Begin nodeTemp = node.right; node.right = nodeTemp.left; If (nodeTemp.left != NIL) Then nodeTemp.left.nodeParent = node; nodeTemp.nodeParent = node.nodeParent; If (node.nodeParent == NIL) Then Tree.root = nodeTemp; Else Begin If (node == node.nodeParent.left) Then node.nodeParent.left = nodeTemp; Else node.nodeParent.right = nodeTemp; End nodeTemp.left = node; node.nodeParent = nodeTemp; End RBTRightRotate(Tree,node) Begin nodeTemp = node.left; node.left = nodeTemp.right; If (nodeTemp.right != NIL) Then nodeTemp.right.nodeParent = node; nodeTemp.nodeParent = node.nodeParent; If (node.nodeParent == NIL) Then Tree.root = nodeTemp; Else Begin If (node == node.nodeParent.right) Then node.nodeParent.right = nodeTemp; Else node.nodeParent.left = nodeTemp; End nodeTemp.right = node; node.nodeParent = nodeTemp; End |
Добавление вершины в КЧД
Чтобы добавить вершину в КЧД, мы применяем процедуру TreeInsert для ДДП, красим вершину в красный цвет, а затем восстанавливаем свойства КЧД. Для этого мы перекрашиваем некоторые вершины и производим вращения.
|
1 RBTInsert(Tree,node) 2 Begin 3 TreeInsert(Tree,node); 4 node.color = RED; 5 While (node != Tree.root) and (node.nodeParent.color == RED) Do 6 Begin 7 If (node.nodeParent == node.nodeParent.nodeParent.left) Then 8 Begin 9 nodeTemp = node.nodeParent.nodeParent.right; 10 If (nodeTemp.color == RED) Then 11 Begin 12 node.nodeParent.color = BLACK; 13 nodeTemp.color = BLACK; 14 node.nodeParent.nodeParent.color = RED; 15 node = node.nodeParent.nodeParent; 16 End 17 Else 18 Begin 19 If (node == node.nodeParent.right) Then 20 Begin 21 node = node.nodeParent; 22 RBTLeftRorate(Tree,node); 23 End 24 node.nodeParent.color = BLACK; 25 node.nodeParent.nodeParent.color = RED; 26 RBTRightRotate(Tree,node.nodeParent.nodeParent); 27 End 28 End 29 Else 30 Begin 31 nodeTemp = node.nodeParent.nodeParent.left; 32 If (nodeTemp.color == RED) Then 33 Begin 34 node.nodeParent.color = BLACK; 35 nodeTemp.color = BLACK; 36 node.nodeParent.nodeParent.color = RED; 37 node = node.nodeParent.nodeParent; 38 End 39 Else 40 Begin 41 If (node == node.nodeParent.left) Then 42 Begin 43 node = node.nodeParent; 44 RBTRightRorate(Tree,node); 45 End 46 node.nodeParent.color = BLACK; 47 node.nodeParent.nodeParent.color = RED; 48 RBTLeftRotate(Tree,node.nodeParent.nodeParent); 49 End 50 End 51 End 52 Tree.root.color = BLACK; 53 End |
Функция RBTInsert не так сложна, как кажется на первый взгляд. Рассмотрим её подробнее. После строк 3-4 выполняются все свойства КЧД, кроме, возможно, одного: у новой красной вершины может быть красный родитель. Такая ситуация (красная вершина имеет красного родителя) может сохраниться после любого числа итераций цикла. Внутри цикла рассматриваются 6 различных случаев, но три из них (строки 8-28) симметричны трём другим (строки 30-50), различие лишь в том, является ли родитель вершины node правым или левым потомком своего родителя (случаи разделяются в строке 7). Поэтому мы рассмотрим подробно только первые три случая (строки 8-28). Предположим, что во всех рассматриваемых КЧД корень чёрный, и будем поддерживать это свойство (строка 52). Поэтому в строке 5 node.nodeParent (красного цвета) не может быть корнем, и node.nodeParent.nodeParent != NIL. Операции внутри цикла начинаются с нахождения nodeTemp, “дяди” node, то есть вершины, имеющей того же родителя, что и node.nodeParent. Если nodeTemp – красная вершина, то имеет место случай 1, если черная, то 2 или 3. Во всех случаях вершина node.nodeParent.nodeParent – чёрная, так как пара node, node.nodeParent была единственным нарушением свойств КЧД.
Случай 1 (строки 12-15 и 34-37) показан на рисунке 6. Является ли вершина node правым или левым потомком своего родителя, значения не имеет.
Рисунок 6.
Обе вершины (node и nodeTemp) – красные, а вершина node.nodeParent.nodeParent – чёрная. Перекрасим node.nodeParent и nodeTemp в чёрный цвет, а node.nodeParent.nodeParent – в красный. При этом число чёрных вершин на любом пути от корня к листьям остаётся прежним. Нарушение свойств КЧД возможно лишь в одном месте: вершина node.nodeParent.nodeParent может иметь красного родителя, поэтому надо продолжить выполнение цикла, присвоив node значение node.nodeParent.nodeParent.
В случаях 2 и 3 вершина nodeTemp – чёрная. Различаются случаи, когда вершина node является правым или левым потомком своего родителя. Если правым, то это случай 2 (строки 20-23 и 41-45). В этом случае производится левое вращение, которое сводит случай 2 к случаю 3, когда node является левым потомком своего родителя. Так как node и node.nodeParent – красные, после вращения количество чёрных вершин на путях от корня к листьям остается прежним.
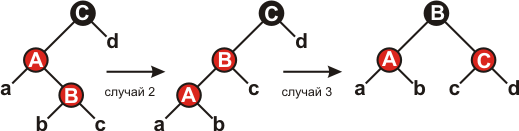
Рисунок 7.
Осталось рассмотреть случай 3: красная вершина node является левым потомком красной вершины node.nodeParent, которая, в свою очередь, является левым потомком node.nodeParent.nodeParent, правым потомком которой является nodeTemp. В этом случае достаточно произвести правое вращение и перекрасить две вершины. Цикл окончится, так как вершина node.nodeParent будет после этого чёрной.
Удаление вершины из КЧД
Удаление вершины немного сложнее добавления. Мы будем считать, что (NIL).color == BLACK, и будем считать операцию взятия цвета у указателя, равного NIL, допустимой операцией. Также мы будем считать допустимым присваивание (NIL).nodeParent, и будем считать данное присваивание имеющим результат. То есть при взятии значения (NIL).nodeParent мы получим ранее записанное значение. Функция RBTDelete подобна TreeDelete, но, удалив вершину, она вызывает процедуру RTBDeleteFixUp для восстановления свойств КЧД.
|
RBTDelete(Tree,node) Begin If (node.left == NIL) or (node.right == NIL) Then nodeParent = node; Else nodeParent = TreeNext(node); If (nodeParent.left != NIL) Then nodeTemp = nodeParent.left; Else nodeTemp = nodeParent.right; nodeTemp.nodeParent = nodeParent.nodeParent; If (nodeTemp.nodeParent == NIL) Then Tree.root = nodeTemp; Else Begin If (nodeParent.nodeParent.left == nodeParent) Then nodeParent.nodeParent.left = nodeTemp; Else nodeParent.nodeParent.right = nodeTemp; End If (nodeParent != node) Then Begin node.key = nodeParent.key; node.color = nodeParent.color; { копирование дополнительных данных } End If (nodeParent.color == BLACK) Then RBTDeleteFixUp(Tree,nodeTemp); Return nodeParent; End |
Рассмотрим, как процедура RBTDeleteFixUp восстанавливает свойства КЧД. Очевидно, что если удалили красную вершину, то, поскольку оба ее потомка чёрные, красная вершина не станет родителем красного потомка. Если же удалили чёрную вершину, то как минимум на одном из путей от корня к листьям количество чёрных вершин уменьшилось. К тому же красная вершина могла стать потомком красного родителя.
|
1 RTBDeleteFixUp(Tree,node) 2 Begin 3 While (node != Tree.root) and (node.color == BLACK) Do 4 Begin 5 If (node == node.nodeParent.left) 6 Begin 7 nodeTemp = node.nodeParent.right; 8 If (nodeTemp.color == RED) Then 9 Begin 10 nodeTemp.color = BLACK; 11 nodeTemp.nodeParent.color = RED; 12 RBTLeftRotate(Tree,node.nodeParent); 13 nodeTemp = node.nodeParent.right; 14 End 15 If (nodeTemp.left.color == BLACK) and (nodeTemp.right.color == BLACK) Then 16 Begin 17 nodeTemp.color = RED; 18 nodeTemp = nodeTemp.nodeParent; 19 End 20 Else 21 Begin 22 If (nodeTemp.right.color == BLACK) Then 23 Begin 24 nodeTemp.left.color = BLACK; 25 nodeTemp.color = RED; 26 RBTRightRotate(Tree,nodeTemp) 27 nodeTemp = node.nodeParent.right; 28 End 29 nodeTemp.color = node.nodeParent.color; 30 node.color.nodeParent = BLACK; 31 nodeTemp.right.color = BLACK; 32 RBTLeftRotate(Tree,node.nodeParent); 33 node = Tree.root; 34 End 35 End 36 Else 37 Begin 38 nodeTemp = node.nodeParent.left; 39 If (nodeTemp.color == RED) Then 40 Begin 41 nodeTemp.color = BLACK; 42 nodeTemp.nodeParent.color = RED; 43 RBTRightRotate(Tree,node.nodeParent); 44 nodeTemp = node.nodeParent.left; 45 End 46 If (nodeTemp.right.color == BLACK) and (nodeTemp.left.color == BLACK) Then 47 Begin 48 nodeTemp.color = RED; 49 nodeTemp = nodeTemp.nodeParent; 50 End 51 Else 52 Begin 53 If (nodeTemp.left.color == BLACK) Then 54 Begin 55 nodeTemp.right.color = BLACK; 56 nodeTemp.color = RED; 57 RBTLeftRotate(Tree,nodeTemp) 58 nodeTemp = node.nodeParent.left; 59 End 60 nodeTemp.color = node.nodeParent.color; 61 node.color.nodeParent = BLACK; 62 nodeTemp.left.color = BLACK; 63 RBTRightRotate(Tree,node.nodeParent); 64 node = Tree.root; 65 End 66 End 67 End 68 node.color = BLACK; 69 End |
Процедура RBTDeleteFixUp применяется к дереву, которое обладает свойствами КЧД, если учесть дополнительную единицу черноты в вершине node (она теперь дважды чёрная, это чисто логическое понятие, и оно нигде фактически не сохраняется и логического типа для хранения цвета вам всегда будет достаточно) и превращает его в настоящее КЧД.
Что такое дважды чёрная вершина? Это определение может запутать. Формально вершина называется дважды чёрной, дабы отразить тот факт, что при подсчёте чёрных вершин на пути от корня до листа эта вершина считается за две черных. Если чёрная вершина была удалена, её черноту так просто выкидывать нельзя. Она на счету. Поэтому временно черноту удалённой вершины передали вершине node. В задачу процедуры RBTDeleteFixUp входит распределение этой лишней черноты. Они или будет передана красной вершине (и та станет чёрной) или после перестановок других чёрных вершин (дабы изменить их количество на пути от корня к листьям) будет просто выкинута.
В цикле (строки 3-67) дерево изменяется, и значение переменной node тоже изменяется, но сформулированное свойство остаётся верным. Цикл завершается, если:
node указывает на красную вершину, тогда мы красим её в чёрный цвет (строка 68).
node указывает на корень дерева, тогда лишняя чернота может быть просто удалена.
Могло оказаться, что внутри тела цикла удается выполнить несколько вращений и перекрасить несколько вершин, так что дважды чёрная вершина исчезает. В этом случае присваивание node = Tree.root (строки 33 и 64) позволяет выйти из цикла.
Внутри цикла node указывает на дважды чёрную вершину, а nodeTemp – на её брата (другую вершину с тем же родителем). Поскольку вершина node дважды чёрная, nodeTemp не может быть NIL, поскольку в этом случае вдоль одного пути от node.nodeParent было бы больше чёрных вершин, чем вдоль другого. Четыре возможных случая показаны на рисунке ниже. Зелёным и синим, помечены вершины, цвет которых не играет роли, то есть может быть как черным, так и красным, но сохраняется в процессе преобразований.
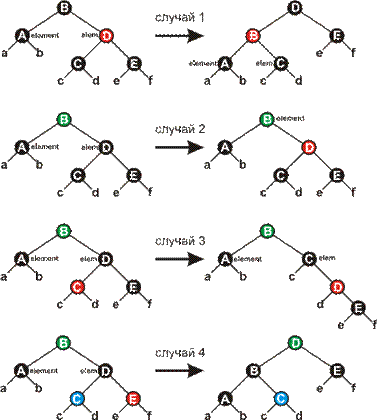
Рисунок 8
Убедитесь, что преобразования не нарушают свойство 4 КЧД (помните, что вершина node считается за две чёрные, и что в поддеревьях a - f изначально не равное количество чёрных вершин).
Случай 1 (строки 9-14 и 40-45) имеет место, когда вершина nodeTemp красная (в этом случае node.nodeParent чёрная). Так как оба потомка вершины nodeTemp чёрные мы можем поменять цвета nodeTemp и node.nodeParent и произвести левое вращение вокруг node.nodeParent не нарушая свойств КЧД. Вершина node остается дважды чёрной, а её новый брат – чёрным, так что мы свели дело к одному из случаев 2-4.
Случай 2 (строки 16-19 и 47-50). Вершина nodeTemp – чёрная, и оба её потомка тоже чёрные. В этом случае мы можем снять лишнюю чёрноту с node (теперь она единожды чёрная), перекрасить nodeTemp, сделав ёё красной (оба её потомка чёрные, так что это допустимо) и добавить черноту родителю node. Заметим, что если мы попали в случай 2 из случая 1, то вершина node.nodeParent – красная. Сделав её чёрной (добавление чёрного к красной вершине делает её чёрной), мы завершим цикл.
Случай 3 (строки 23 – 28 и 53 - 59) Вершина nodeTemp чёрная, её левый потомок красный, а правый чёрный. Мы можем поменять цвета nodeTemp и её левого потомка и потом применить правое вращение так, что свойства КЧД будут сохранены. Новым братом node будет теперь чёрная вершина с красным правым потомком, и случай 3 сводится к случаю четыре.
Случай 4 (строки 29 – 33 и 60 - 64) Вершина nodeTemp чёрная, правый потомок красный. Меняя некоторые цвета (не все из них нам известны, но это нам не мешает) и, производя левое вращение вокруг node.nodeParent, мы можем удалить лишнюю черноту у node, не нарушая свойств КЧД. присваивание node = Tree.root выводит нас из цикла.
Сравнительные характеристики скорости работы различных структур данных
Чтобы всё сказанное до этого не казалось пустой болтовнёй, я в качестве заключения приведу сравнительные характеристики скорости работы различных структур данных (деревьев и массивов). Для измерения времени была использована функция WinAPI QueryPerfomanceCounter. Время пересчитано в микросекунды. В скобках приведена конечная глубина дерева. Тестирование проводилось на процессоре Intel Celeron Tualatin 1000MHz с 384Мб оперативной памяти. В качестве ключа использовалось число типа int (32-х битное целое со знаком), а в качестве данных число типа float (4-х байтное вещественное).
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Несортированный массив | Массив с постсортировкой |
| 1000 |
4943 (1000) |
535 (17) |
193 | 32 | 73 |
| 2000 |
20571 (2000) |
1127 (19) |
402 | 89 | 152 |
| 3000 |
65819 (3000) |
1856 (20) |
621 | 98 | 305 |
| 4000 |
82321 (4000) |
2601 (21) |
862 | 189 | 327 |
| 5000 |
126941 (5000) |
3328 (22) |
1153 | 192 | 461 |
| 6000 |
183554 (6000) |
4184 (22) |
1391 | 363 | 652 |
| 7000 |
255561 (7000) |
4880 (23) |
1641 | 452 | 789 |
| 8000 |
501360 (8000) |
5479 (23) |
1905 | 567 | 874 |
| 9000 |
1113230 (9000) |
6253 (24) |
2154 | 590 | 1059 |
| 10000 |
1871090 (10000) |
7174 (24) |
2419 | 662 | 1180 |
Таблица 1. Добавление элемента (возрастающие ключи)
| Количество элементов | ДДП | КЧД |
Постоянно сортированный массив |
Несортированный массив | Массив с постсортировкой |
| 1000 | 4243 | 108 | 136 | 1354 | 134 |
| 2000 | 19295 | 250 | 289 | 5401 | 286 |
| 3000 | 71271 | 391 | 448 | 25373 | 441 |
| 4000 | 79819 | 560 | 615 | 23861 | 607 |
| 5000 | 124468 | 759 | 787 | 38862 | 776 |
| 6000 | 180029 | 956 | 954 | 55303 | 941 |
| 7000 | 246745 | 1199 | 1165 | 75570 | 1111 |
| 8000 | 487187 | 1412 | 1307 | 98729 | 1330 |
| 9000 | 1062128 | 1906 | 1494 | 134470 | 1474 |
| 10000 | 1807235 | 2068 | 1719 | 154774 | 1688 |
Таблица 2. Поиск элемента (возрастающие ключи).
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Несортированный массив | Массив с постсортировкой |
| 1000 | 308 | 419 | 2077 | 2047 | 2080 |
| 2000 | 639 | 876 | 13422 | 8046 | 8179 |
| 3000 | 1001 | 1372 | 25092 | 30902 | 18407 |
| 4000 | 1380 | 1831 | 32572 | 32473 | 32651 |
| 5000 | 1680 | 2286 | 50846 | 51001 | 50962 |
| 6000 | 2105 | 2891 | 73321 | 73114 | 73202 |
| 7000 | 2569 | 3514 | 99578 | 100059 | 99801 |
| 8000 | 3025 | 4384 | 129833 | 129897 | 130054 |
| 9000 | 3484 | 5033 | 164846 | 194361 | 164264 |
| 10000 | 4050 | 5690 | 203207 | 202979 | 202738 |
Таблица 3. Удаление элемента по ключу (возрастающие ключи).
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Несортированный массив | Массив с постсортировкой |
| 1000 |
547 (25) |
548 (13) |
1800 | 34 | 362 |
| 2000 |
1133 (25) |
1171 (14) |
5534 | 70 | 734 |
| 3000 |
1723 (28) |
1905 (14) |
12065 | 150 | 1174 |
| 4000 |
2891 (28) |
2985 (15) |
20867 | 223 | 1626 |
| 5000 |
3604 (28) |
4024 (15) |
32927 | 248 | 1962 |
| 6000 |
4336 (29) |
4970 (15) |
44720 | 373 | 2537 |
| 7000 |
5196 (29) |
5794 (16) |
60723 | 443 | 2977 |
| 8000 |
6051 (30) |
6972 (16) |
77482 | 511 | 3485 |
| 9000 |
6994 (30) |
7519 (16) |
104219 | 590 | 3821 |
| 10000 |
9544 (31) |
10303 (16) |
118760 | 584 | 4408 |
Таблица 4. Добавление элемента (случайные ключи)
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Несортированный массив | Массив с постсортировкой |
| 1000 | 181 | 136 | 159 | 1354 | 155 |
| 2000 | 406 | 307 | 347 | 5412 | 339 |
| 3000 | 653 | 494 | 551 | 12927 | 538 |
| 4000 | 925 | 702 | 765 | 23936 | 747 |
| 5000 | 1223 | 949 | 1024 | 37861 | 962 |
| 6000 | 1532 | 1142 | 1216 | 55124 | 1185 |
| 7000 | 1893 | 1494 | 1453 | 75628 | 1403 |
| 8000 | 2477 | 1833 | 1679 | 98802 | 1631 |
| 9000 | 2943 | 2390 | 1994 | 125570 | 1858 |
| 10000 | 3395 | 2937 | 2228 | 154791 | 2108 |
Таблица 5. Поиск элемента (случайные ключи)
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Несортированный массив | Массив с постсортировкой |
| 1000 | 469 | 517 | 1149 | 2014 | 1195 |
| 2000 | 995 | 1079 | 4381 | 8054 | 4387 |
| 3000 | 1557 | 1756 | 9673 | 18191 | 9639 |
| 4000 | 2272 | 2424 | 17071 | 32451 | 17105 |
| 5000 | 3070 | 3019 | 27380 | 50665 | 26954 |
| 6000 | 3528 | 3618 | 39294 | 72996 | 39227 |
| 7000 | 4322 | 4542 | 53255 | 99402 | 53309 |
| 8000 | 5299 | 5531 | 71406 | 129964 | 70766 |
| 9000 | 6180 | 6553 | 89583 | 164943 | 89935 |
| 10000 | 7527 | 7797 | 112190 | 202993 | 111439 |
Таблица 6. Удаление элемента по ключу (случайные ключи)
Постоянно сортированный массив – это массив, в который элементы вставляются так, что бы он сохранял свойство упорядоченности. Массив с постсортировкой – это массив, в который сначала вставляются все элементы, а потом он сортируется алгоритмом быстрой сортировки. Данные таблицы, безусловно, не являются истиной в последней инстанции, но позволят вам прикинуть, какая из структур данных будет наиболее производительна в вашей программе, учитывая предполагаемую вероятность операций вставки, удаления и поиска. Так, например, массив с постсортировкой является весьма привлекательным по производительности, но совершенно не подходит для комплексных работ, так как предполагает фиксированный порядок действий – сначала только добавление элементов, а после использование полученной информации. Другие структуры данных лишены этого недостатка. Для большого числа (порядка 10 000) случайных элементов время поиска в ДДП и КЧД становится практически одинаковым. Как следствие, можно реализовать более простые алгоритмы, исходя из некоторых свойств входных данных. С другой стороны, в крайнем случае (возрастающие элементы) ДДП отстают от КЧД на несколько порядков. Постоянно сортированный массив является абсолютным победителем по скорости, но не имеет естественной поддержки отношений родитель-ребёнок. Если они вам нужны, придётся реализовывать их поддержку самостоятельно. Также надо всегда помнить, что при количестве элементов порядка тысячи, асимптотические показатели скорости ещё не вполне вступили в силу и теоретически более быстрые структуры данных на практике могут оказаться более медленными. Так, например, скорость поиска в КЧД и массиве с пресортировкой до 5000-7000 практически одинакова. Так же надо заметить, что тестирование производилось на объектах относительно малого размера (8 байт), сравнимого с размером указателя (4 байта). Все виды массивов сортированных подразумевают весьма интенсивное копирование элементов, в то время как деревья работают с указателями. При размере элемента, на порядки превышающем размеры указателя, акценты сместятся весьма значительно. Например, ниже приведены результаты испытания с ключом типа int (32-x битное целое) и битовыми данными размером в 256 байт.
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Не сортированный массив | Массив с постсортировкой |
| 1000 |
5868 (1000) |
1663 (17) |
1430 | 1154 | 1035 |
| 2000 |
140888 (2000) |
3694 (19) |
3476 | 2460 | 2808 |
| 3000 |
368748 (3000) |
5815 (20) |
5372 | 3848 | 4382 |
| 4000 |
721328 (4000) |
7271 (21) |
7274 | 5175 | 6035 |
| 5000 |
1208373 (5000) |
9349 (22) |
9247 | 6670 | 7619 |
| 6000 |
1752135 (6000) |
11395 (22) |
11046 | 7778 | 9168 |
| 7000 |
2501167 (7000) |
13503 (23) |
13327 | 9378 | 10764 |
| 8000 |
3334948 (8000) |
15753 (23) |
18222 | 12560 | 15267 |
| 9000 |
4266560 (9000) |
21600 (24) |
20564 | 15391 | 17430 |
| 10000 |
5421499 (10000) |
24105 (24) |
24064 | 17152 | 19341 |
Таблица 7. Добавление элемента (возрастающие ключи)
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Не сортированный массив | Массив с постсортировкой |
| 1000 | 4289 | 132 | 242 | 1621 | 230 |
| 2000 | 134074 | 303 | 605 | 6903 | 530 |
| 3000 | 359985 | 457 | 961 | 24268 | 806 |
| 4000 | 706129 | 787 | 1336 | 27610 | 1121 |
| 5000 | 1183405 | 959 | 1736 | 44660 | 1516 |
| 6000 | 1730699 | 1116 | 2138 | 69068 | 1841 |
| 7000 | 2462759 | 1344 | 2494 | 103158 | 2251 |
| 8000 | 3293519 | 1565 | 2871 | 159274 | 2617 |
| 9000 | 4215750 | 1840 | 3284 | 278697 | 2923 |
| 10000 | 5361524 | 2060 | 3698 | 513268 | 3303 |
Таблица 8. Поиск элемента (возрастающие ключи)
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Не сортированный массив | Массив с постсортировкой |
| 1000 | 502 | 583 | 115640 | 131837 | 186703 |
| 2000 | 1181 | 1152 | 1604342 | 1574484 | 1592896 |
| 3000 | 1602 | 1580 | 4616940 | 4653355 | 4604626 |
| 4000 | 2075 | 2537 | 8966113 | 8999484 | 8978279 |
| 5000 | 2689 | 3007 | 14848795 | 14851393 | 14822206 |
| 6000 | 3574 | 3836 | 21572736 | 21473162 | 21676597 |
| 7000 | 4129 | 4432 | 30384061 | 29938188 | 30409709 |
| 8000 | 4898 | 5424 | 39013182 | 39342862 | 39341616 |
| 9000 | 5086 | 6368 | 50197296 | 49946077 | 50320092 |
| 10000 | 6279 | 6372 | 63020912 | 62049584 | 62564125 |
Таблица 9. Удаление элемента по ключу (возрастающие ключи)
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Не сортированный массив | Массив с постсортировкой |
| 1000 |
1903 (24) |
2072 (12) |
57991 | 1418 | 5448 |
| 2000 |
4532 (25) |
4739 (14) |
479463 | 3107 | 13907 |
| 3000 |
7747 (26) |
7819 (15) |
1727433 | 4992 | 22440 |
| 4000 |
10348 (29) |
10664 (15) |
3616654 | 6733 | 33905 |
| 5000 |
13064 (29) |
13652 (16) |
6141684 | 8314 | 43768 |
| 6000 |
16530 (31) |
16713 (16) |
9214638 | 10191 | 53619 |
| 7000 |
19305 (31) |
19642 (16) |
12981887 | 11904 | 61301 |
| 8000 |
23140 (32) |
23329 (16) |
17388765 | 13785 | 75968 |
| 9000 |
26051 (32) |
26378 (16) |
21935279 | 15335 | 92007 |
| 10000 |
29450 (32) |
29448 (16) |
27053495 | 17075 | 90155 |
Таблица 10. Добавление элемента (случайные ключи)
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Не сортированный массив | Массив с постсортировкой |
| 1000 | 185 | 150 | 266 | 1613 | 274 |
| 2000 | 695 | 359 | 719 | 6974 | 724 |
| 3000 | 1044 | 586 | 1193 | 15561 | 1245 |
| 4000 | 2186 | 823 | 1694 | 27675 | 1703 |
| 5000 | 2701 | 1106 | 2234 | 44905 | 2314 |
| 6000 | 3898 | 1496 | 2874 | 71549 | 2871 |
| 7000 | 4883 | 1889 | 3464 | 109554 | 3371 |
| 8000 | 4186 | 2183 | 4060 | 165605 | 4077 |
| 9000 | 6760 | 2771 | 4696 | 281860 | 4622 |
| 10000 | 7291 | 3201 | 5372 | 514893 | 5384 |
Таблица 11. Поиск элемента (случайные ключи)
| Количество элементов | ДДП | КЧД | Постоянно сортированный массив | Не сортированный массив | Массив с постсортировкой |
| 1000 | 1235 | 1115 | 54929 | 111088 | 62794 |
| 2000 | 3042 | 2978 | 557875 | 1596298 | 558580 |
| 3000 | 4641 | 4703 | 1837401 | 4730623 | 1841029 |
| 4000 | 7531 | 6494 | 3830510 | 9008129 | 3833983 |
| 5000 | 9497 | 8788 | 6675616 | 14599142 | 6626964 |
| 6000 | 12018 | 10922 | 10270460 | 21832592 | 10315160 |
| 7000 | 14605 | 14376 | 14808484 | 29779691 | 14618091 |
| 8000 | 15876 | 16070 | 19927348 | 39932636 | 19946118 |
| 9000 | 20043 | 19079 | 25347571 | 49928153 | 25384886 |
| 10000 | 22117 | 21860 | 32049086 | 61766884 | 32072537 |
Таблица 12. Удаление элемента по ключу (случайные ключи)
Хорошо видно, что при увеличенном размере элемента деревья догоняют, а то и значительно обгоняют массивы. Таким образом, очевидно, что выбор структуры данных сильно зависит от предполагаемого количества элементов и их размера. Напоследок хотелось бы сказать, что правильный выбор структуры данных является одним из основных моментов, определяющих производительность программы. Поэтому подходить к выбору надо осторожно, продумав все возможные - как наиболее вероятные, так и наихудшие случаи.