Реферат: Ядерный магнитный резонанс (ЯМР)

1. Введение.

1.1. Из истории спектроскопии магнитного резонанса.

     До недавнего времени основой наших представлений о структуре атомов и молекул служили исследования методами оптической спектроскопии. В связи с усовершенствованием спектральных методов, продвинувших область спектроскопических измерений в диапазон сверхвысоких (примерно 103 - 106 МГц; микрорадиоволны) и высоких частот (примерно 10-2 - 102 МГц; радиоволны), появились новые источники информации о структуре вещества. При поглощении и испускании излучения в этой области частот происходит тот же основной процесс, что и в других диапазонах электромагнитного спектра, а именно при переходе с одного энергетического уровня на другой система поглощает           или испускает квант          энергии.
    Разность энергий уровней и энергия квантов, участвующих в этих процессах, составляют около 10-7 эВ для области радиочастот и около 10-4 эВ для     сверхвысоких         частот.
    Существование ядерных моментов впервые было обнаружено при изучении сверхтонкой структуры электронных спектров некоторых атомов с помощью оптических спектрометров с высокой разрешающей способностью.

Сверхтонкая структура атомных спектров навела Паули в 1924 г. на мысль о том, что некоторые ядра обладают моментом количества движения (угловым моментом), а, следовательно, и магнитным моментом, взаимодействующим с атомными орбитальными электронами. Впоследствии эта гипотеза была подтверждена спектроскопическими измерениями, которые позволили определить значения угловых и магнитных моментов для многих ядер.
Под влиянием внешнего магнитного поля магнитные моменты ядер ориентируются определенным образом, и появляется возможность наблюдать переходы между ядерными энергетическими уровнями, связанными с этими разными ориентациями: переходы, происходящие под действием излучения определенной частоты. Квантование энергетических уровней ядра является прямым следствием квантовой природы углового момента ядра, принимающего 2I + 1 значений. Спиновое квантовое число (спин) I может принимать любое значение, кратное 1/2; наиболее высоким из известных значений I (≥7) обладает 17671Lu. Измеримое наибольшее значение углового момента (наибольшее значение проекции момента на выделенное направление) равно Iħ, где ħ=h/2π, а h - постоянная Планка.
Значения I для конкретных ядер предсказать нельзя, однако было замечено, что изотопы, у которых и массовое число, и атомный номер четные, имеют I = 0, а изотопы с нечетными массовыми числами имеют полуцелые значения спина. Такое положение, когда числа протонов и нейтронов в ядре четные и равны (I = 0), можно рассматривать как состояние с "полным спариванием", аналогичным полному спариванию электронов в диамагнитной молекуле.

В 1921г. Штерн и Герлах методом атомного пучка показали, что измеримые значения магнитного момента атома дискретны соответственно пространственному квантованию атома в неоднородном магнитном поле. В последующих экспериментах, пропуская через постоянное магнитное поле пучок молекул водорода, удалось измерить небольшой по величине магнитный момент ядра водорода. Дальнейшее развитие метода состояло в том, что на пучок воздействовали дополнительным магнитным полем, осциллирующим с частотой, при которой индуцируются переходы между ядерными энергетическими уровнями, соответствующими квантовым значениям ядерного магнитного момента.

Если ядерное спиновое число равно I, то ядро имеет (2I+1) равноотстоящих энергетических уровней; в постоянном магнитном поле с напряженностью H расстояние между наивысшим и наинизшим из этих уровней равно 2mH, где m- максимальное измеримое значение магнитного момента ядра. Отсюда расстояние между соседними уровнями равно mH/I, а частота осциллирующего магнитного поля, которое может вызвать переходы между этими уровнями, равна mH/Ih.

В эксперименте с молекулярным пучком до детектора доходят те молекулы, энергия которых не меняется. Частота, при которой происходят резонансные переходы между уровнями, определяется путем последовательного изменения (развертки) частоты в некотором диапазоне. На определенной частоте происходит внезапное уменьшение числа молекул, достигающих детектора.

Первые успешные наблюдения ЯМР такого рода были выполнены с основными магнитными полями порядка нескольких кило эрстед, что соответствует частотам осциллирующего магнитного поля в диапазоне 105-108 Гц. Резонансный обмен энергией может происходить не только в молекулярных пучках; его можно наблюдать во всех агрегатных состояниях вещества.

В 1936г. Горнер пытался обнаружить резонанс ядер Li7 во фтористом литии и ядер H1 в алюмокалиевых квасцах. Другая безуспешная попытка была предпринята гортнером и Бруром в 1942г. Регистрацию поглощения высокочастотной энергии при резонансе в этих экспериментах предполагалось производить соответственно калориметрическим методом и по аномальной дисперсии. Основной причиной неудач этих опытов был выбор неподходящих объектов. Лишь в конце 1945 года двумя группами американских физиков под руководством Ф. Блоха и Э.М. Пурселла впервые были получены сигналы ядерного магнитного резонанса. Блох наблюдал резонансное поглощение на протонах в воде, а Парселл добился успеха в обнаружении ядерного резонанса на протонах в парафине. За это открытие они в 1952 году были удостоены Нобелевской премии.

1.2.Технологичекие приложения ЯМР (основные достоинства метода ЯМР).

Метод ЯМР, хотя он и называется методом ядерного магнитного резонанса, не имеет никакого отношения к ядерной физике, которая, как известно, изучает процессы превращения ядер, т.е. радиоактивные процессы. При этом магнитная энергия (а явление ЯМР имеет место при помещении исследуемого образца в постоянное магнитное поле) не влияет на термодинамические свойства вещества, т.к. она во много раз (а точнее - на несколько порядков) меньше тепловой энергии, характерной для происходящих в обычных условиях процессов, в том числе и биологических.

Основные достоинства метода ЯМР.

- Высокая разрешающая способность – на десять порядков больше, чем у оптической спектроскопии.

- Возможность вести количественный учет (подсчет) резонирующих ядер. Это открывает возможности для количественного анализа вещества.

- Спектры ЯМР зависят от характера процессов, протекающих в исследуемом веществе. Поэтому эти процессы можно изучать указанным методом. Причем доступной оказывается временная шкала в очень широких пределах – от многих часов до малых долей секунды.

- Современная радиоэлектронная аппаратура и ЭВМ позволяют получать параметры, характеризующие явление, в удобной для исследователей и потребителей метода ЯМР форме. Данное обстоятельство особенно важно, когда речь идет о практическом использовании экспериментальных данных.

Главным преимуществом ЯМР по сравнении с другими видами спектроскопии является возможность преобразования и видоизменения ядерного спинового гамильтониана по воле экспериментатора практически без каких-либо ограничений и подгонки его под специальные требования решаемой задачи. Из-за большой сложности картины не полностью разрешенных линий многие инфракрасные и ультрафиолетовые спектры невозможно расшифровать. Однако в ЯМР преобразование гамильтониана таким образом, чтобы можно было подробно проанализировать спектр, во многих случаях позволяет упростить сложные спектры.

То, с какой легкостью удается преобразовать ядерный спиновый гамильтониан, обусловлено определенными причинами. Благодаря тому, что ядерные взаимодействия являются слабыми, можно ввести сильные возмущения, достаточные для того, чтобы подавить нежелательные взаимодействия. В оптической спектроскопии соответствующие взаимодействия обладают значительно большей энергией и подобные преобразования фактически невозможны.

Модификация спинового гамильтониана играет существенную роль во многих приложениях одномерной ЯМР - спектроскопии. В настоящее время широкое распространение получило упрощение спектров или повышение их информативности с помощью спиновой развязки, когерентного усреднения многоимпульсными последовательностями, вращения образцов или частичной ориентации в жидкокристаллических растворителях.

Говоря о достоинствах приборов ЯМР, необходимо исходить из реальных возможностей в приобретении и эксплуатации ЯМР-спектрометров. В этой связи необходимо отметить следующее.

Операторские обязанности при работе на этих спектрометрах может выполнять любой человек. Но само обслуживание и ремонт требуют высокой квалификации.

Проведение экспериментов по ЯМР сводится к следующему. Исследуемый образец помещают в постоянное магнитное поле, которое создается постоянным магнитом или, чаще всего, электромагнитом.

При этом на образец подается радиочастотное излучение, обычно метрового диапазона. Резонанс детектируется соответствующими радиоэлектронными устройствами, обрабатывается ими и выдается в виде спектрограммы, которая может быть выедена на осциллограф или самописец, в виде ряда цифр и таблиц, получаемых с помощью печатающего устройства. Выходной резонансный сигнал может быть также введен в тот или иной технологический процесс для управления этим процессом или циклом.

Обычно, если речь идет об исследовании в стационарных условиях моно мерных соединений на ядрах водорода с молекулярной массой несколько сотен единиц (а таких веществ при исследовании большинство), масса исследуемого образца должна быть от нескольких миллиграммов до ста миллиграммов. Образец обычно растворяют в том или ином растворителе, причем объем раствора 0.7¸1 мм3 . При детектировании сигналов ЯМР от других (помимо Н1) ядер масса образца может достигать двух граммов. Если исследуемое вещество – жидкость, то, естественно, готовить раствор в этом случае не обязательно – все зависит от целей эксперимента.

С помощью спектрометров работающих в импульсном режиме можно детектировать сигналы ЯМР от любого сколь угодно малого количества вещества. Конечно, в этом случае требуется просто больше времени, чтобы получить достаточно надежные экспериментальные результаты.

Многие вещества, как известно, не растворяются или растворяются ограниченно. В этом случае сигнал ЯМР можно зарегистрировать от твердой фазы. Требуемая навеска исследуемого образца- до трех граммов. Уместно здесь отметить, что в процессе эксперимента образец не разрушается и может быть использован впоследствии для других целей.

Высокая специфичность и оперативность метода ЯМР, отсутствие химического воздействия на образец, возможность непрерывного измерения параметров открывают многообразные пути его применения в промышленности.

Внедрению метода ЯМР препятствовали :сложность аппаратуры и ее эксплуатации, высокая стоимость спектрометров, исследовательский характер самого метода.

2.Общая теория ядерного магнитного резонанса.

2.1.Классическое описание условий магнитного резонанса.

Вращающийся заряд q можно рассматривать как кольцевой ток, поэтому он ведет себя как магнитный диполь, величина момента равна:

m=iS, (2.1)

где i-сила эквивалентного тока;

S - площадь, охватываемая кольцевым током.

В соответствии с понятием силы тока имеем:

i=qn,

где n=v/2pr-число оборотов заряда q в секунду;

v-линейная скорость;

r-радиус окружности, по которой движется заряд.

Если перейти к электромагнитным единицам (т.е. разделить заряд на с) и учесть, что S=pr2, то выражение (2.1) можно переписать в следующем виде:

m=qvr/2c. (2.2)

Вращающаяся частица с массой М обладает угловым моментом (или моментом импульса)L, представляющим собой вектор, направленный вдоль оси вращения и имеющий величину Mvr. Здесь L=[rp]=[rv], в данном случае r^v. И заряд, и масса участвуют в одном и том же вращении (вращательном движении), поэтому вектор магнитного момента коллинеарен вектору углового момента, с которым он связан соотношением

=(q/2Mc)L=gL, (2.3)

где g=q/2Mc-гиромагнитное отношение, являющееся индивидуальной характеристикой частицы (ядра).

Рассматриваемая здесь модель, естественно, не может объяснить ни наличие магнитного момента у нейтральной частицы (например, у нейтрона), ни отрицательных магнитных моментов некоторых ядер. Тем не менее, изучение классического движения магнитного диполя в магнитном поле позволяет получить дополнительные (по сравнению с квантово-механическим рассмотрением) сведения о природе магнитного резонансного поглощения, особенно при рассмотрении нестационарных явлений. Недостатки классической модели указывают на сложность структуры ядра: полный угловой момент ядра получается в результате сложения в различных комбинациях орбитальных и спиновых движений частиц, входящих в состав ядра. Это сложение аналогично связи спиновых и орбитальных моментов электронов в атомах и молекулах.

Выражение 2.3 позволяет записать классическое уравнение движения магнитного момента в векторной форме следующим образом:

d/dt=g[], (2.4)

где –напряженность внешнего магнитного поля.

Если в отсутствии магнитного поля вращать вектор с угловой скоростью , то, в соответствии с законом Ньютона для вращательного движения, выражение для d/dt будет иметь вид:

d/dt=[]. (2.5)

Из сопоставления выражений 2.4 и 2.5 следует, что действие магнитного поля в точности эквивалентно вращению момента с угловой скоростью =-g (2.6), т.е. ω=gH, или n=gH/2p (2.7), здесь n [Гц] ,H [Э] (уместно вспомнить, что [ab]=-[ba]).

Таким образом, в постоянном магнитном поле вектор магнитного момента будет прецессировать вокруг направления вектора с постоянной угловой скоростью -g независимо от направления вектора , т.е. от угла между осью вращения частицы и направлением поля (рис.1).Угловой скоростью такой прецессии называют ларморовой частотой, а выражение 2.6 – формулой Лармора.

Если перейти к системе координат, вращающейся равномерно с угловой скоростью -g, то при отсутствии других магнитных полей вектор магнитного момента в этой системе координат будет оставаться неизменным по величине и направлению. Другими словами, во вращающейся системе координат постоянное магнитное поле как будто отсутствует.

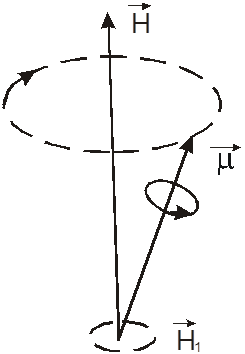
Рис.1. Прецессия магнитного момента в магнитном поле

Допустим теперь, что кроме поля введено другое, более слабое поле 1, постоянное по величине и равномерно вращающееся в плоскости, перпендикулярной направлению (рис.1). Если скорость вращения поля 1 не равна частоте ларморовой прецессии, то это поле будет вращаться и в упомянутой выше вращающейся системе координат. Наличие поля приводит к появлению момента сил [1], который стремится повернуть ядерный момент в плоскость, перпендикулярную . Если направление 1 во вращающейся системе координат меняется, то направление соответствующего момента сил будет быстро меняться, и единственным результатом будут слабые периодические возмущения прецессии магнитного момента.

Если, однако, само поле 1 вращается с ларморовой частотой, то во вращающейся системе координат оно будет вести себя подобно постоянному полю. Поэтому направление момента сил будет оставаться неизменным, что вызовет сильные колебания направления магнитного момента, т.е. большие изменения угла между и 0. При изменении угловой скорости вращения поля 1 колебания с наибольшей амплитудой возникают при совпадении этой скорости с ларморовой частотой. В этом случае говорят о явлении резонанса.

Аналогичное явление резонанса должно наблюдаться, когда направление поля 1 фиксировано, а величина его меняется по синусоидальному закону с частотой, близкой к частоте ларморовой прецессии. Это происходит потому, что такое поле можно представить в виде суперпозиции двух равных полей, вращающихся с равными угловыми скоростями в противоположных направлениях (рис.2). При этом поле, вращающееся в направлении, противоположном направлению ларморовой прецессии, не будет оказывать влияния на резонанс.

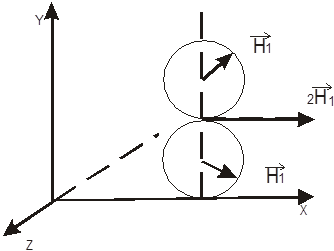
Рис.2. Разложение вектора магнитного поля на два вектора, вращающиеся в противоположные стороны.

На практике для создания магнитного поля, осциллирующего вдоль определенного направления, например, вдоль оси х, по катушке, ось которой перпендикулярна полю 0 и направлена вдоль оси х, пропускают переменный ток. Напряжение с частотой w, приложенное к катушке, создает поле, эквивалентное двум вращающимся в противоположных направлениях полям величиной (Н1cos wt+H1sin wt) и (H1cos wt – H1sin wt).

Если w соответствует частоте резонанса, магнитный диполь поглощает энергию поля, создаваемого катушкой, вследствие чего вектор магнитного момента отклоняется в направлении к плоскости ху и во второй (приемной) катушке, расположенной вдоль оси у, наводится э.д.с.

Т.о., рассмотренная здесь классическая модель резонанса, объясняя суть явления, указывает и на экспериментальное его проявление, состоящее в непрерывном поглощении электромагнитной энергии поля Н1.

2.2.Квантово-механическое рассмотрение условий резонанса.

При включении магнитного поля 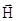каждое ядро приобретает дополнительную энергию -m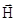, которую называют зеемановской. Гамильтониан в этом случае имеет очень простой вид

H=-m (2.8)

Направляя ось z вдоль приложенного постоянного магнитного поля 0, получаем

H=-gh0Iz (2.9)

Собственные значения этого гамильтониана являются произведениями величины gh0 на собственные значения оператора Iz . поэтому возможные значения энергии равны

Е=-gh0m , m= I , I-1 , … , -I . (2.10)

Чаще всего для наблюдения магнитного резонанса применяют переменное магнитное поле, направленное перпендикулярно постоянному полю. Если амплитуду переменного поля обозначить через H0x, то часть полного гамильтониана, приводящая к переходам, будет иметь вид

Hвозм=-gh0xIxcoswt (2.11)

Оператор Ixимеет отличные от нуля матричные элементы (m’êIx êm), связывающие состояния m и m’, только в случае выполнения равенства m’=m+\-1. В соответствии с этим разрешены переходы только между соседними уровнями, что дает

hw=DE=gh0 (2.12)

или

w=g0 (2.13)

Это соотношение позволяет вычислить частоту, при которой можно наблюдать резонанс, если известно, каким образом можно определить g.

Вычислим магнитный и механический моменты частицы массой mи заряда e, движущейся по окружности радиуса r с периодом Т. В этом случае механический момент

J=mvr=m(2pr2/T), (2.14)

а магнитный момент

m=iA (2.15)

(рассматриваем систему как контур тока i, охватывающий площадь А). Поскольку i= (e/c)(1/T), получаем

m=(е/c)(pr2/T). (2.16)

Сравнение вычисленных значений m и J дает g=m/J=e/2mc. Помимо оценки порядка величины g эта формула позволяет сделать вывод о том, что g для ядер должна быть на три порядка меньше величины g для электронов. Следует пользоваться самыми сильными магнитными полями, какие могут быть получены в лабораторных условиях, т.к. при этом возрастает величина поглощаемых квантов, и сигнал резонанса увеличивается.

Эксперимент Штерна – Герлаха.

Существенным для понимания свойств магнитного момента микрочастиц является его квантование, т.е. наличие у микрочастицы дискретных состояний с различными магнитными свойствами.

Классический эксперимент по доказательству дискретных свойств магнитного момента был впервые осуществлен Штерном и Герлахом. Простейшая схема этого опыта, проведенного сначала для электрона, состоит в следующем (рис.3.). Катод, на который нанесен слой натрия, разогревается в вакууме. Пучок атомов натрия с помощью системы фокусирующих щелей направляется в пространство между полюсами магнита, магнитное поле которого неоднородно; в частности, компонента поля Нz (вдоль оси магнита) зависит от z-координаты, т.е. дНz/дz ≠ 0. за магнитом располагают пластину, на которой регистрируют пучок атомов натрия. Если магнитное поле отсутствует, то пучок фокусируется в центре пластины (Δl=0). Если предположить, что 2s-электрон атома натрия обладает собственным магнитным моментом μе, то при наложении неоднородного магнитного поля на электрон будет действовать сила F, проекция которой на ось z равна

Fz=(μe)z*(дН/дz), (2.17)

где (μе )z – проекция магнитного момента электрона на ось z . эта сила будет вызывать отклонение пучка от центра. Т.о., измерение величины отклонения пучка Δl можно использовать для определения величины проекции магнитного момента электрона (μе)z.

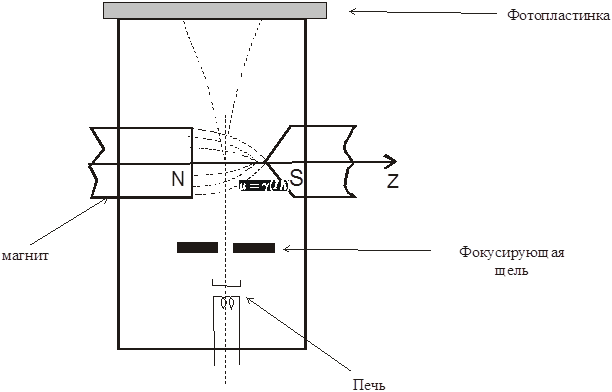
Рис.3. Схема эксперимента Штерна – Герлаха.

Наиболее интересный результат этих экспериментов состоит в том, что на пластине обнаруживается две компоненты (дуплет), расположенные слева и справа от центра на расстояниях ±Δl. Этот результат свидетельствует о наличии у ансамбля частиц двух подсистем, характеризующихся разными значениями проекции магнитного момента ±(μе)z.

При определенных модификациях, вызванных главным образом исключительной малостью ядерных магнитных моментов, эксперименты Штерна – Герлаха могут быть проведены и для случая ядер. При этом, однако, оказывается, что для некоторых ядер наблюдается не две, а большее число компонент.

2.3. Спин- решеточная релаксация.

Ядерные спины всегда взаимодействуют со своим окружением (решеткой), но вследствие того, что это взаимодействие мало, допустимо различать спиновую температуру и температуру решетки. Однако, благодаря имеющемуся слабому взаимодействию между двумя системами, устанавливается тепловое равновесие. Поэтому необходимо рассмотреть скорость установления равновесия. Этот процесс играет существенную роль для установления природы ЯМР.

Рассмотрим систему ядер, помещенную в постоянное магнитное поле 0 (поле 1 отсутствует). Для термического перехода, помимо взаимодействия системы спинов ядер с решеткой, требуется существование определенного энергетического состояния этой системы (решетки), при котором возможен переход. Это можно проиллюстрировать, предположив, что резервуар (решетка) имеет только два уровня энергии, расстояние между которыми точно такое же, как и у ядерной системы.

Если ядро и резервуар вначале находятся в противоположных состояниях (рис. 4а), то одновременный переход, указанный стрелками, удовлетворяет закону сохранения энергии. Следовательно, ядро может отдавать энергию решетке. С другой стороны, если обе системы находятся в верхнем состоянии (рис. 4б), то одновременный переход невозможен, т.к. при этом не сохраняется энергия. Вероятности переходов с поглощением и испусканием одинаковы. При наличии спин- решеточного взаимодействия это равенство нарушается, т.к. в этом случае скорость ядерного перехода зависит от вероятности того, что резервуар находится в состоянии, при котором возможен переход.

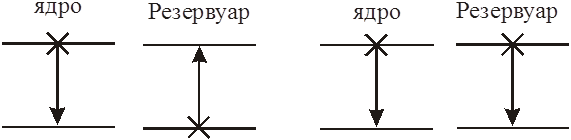
Рис.4. Переходы: а - разрешенный; б - запрещенный.

Возвращаясь к нашей системе, получим:

(n – nравн.)=(n – nравн.)0exp(- t/T1), (2.18)

n – разность заселенности двух уровней или избыток заселенности.

Т.о., разность между избыточным числом ядер в произвольный момент времени и его значение в состоянии теплового равновесия (т.е. к моменту, когда t=Т1) уменьшится в е раз. Это время характеризует скорость, с которой система ядерных спинов приходит в тепловое равновесие с другими степенями свободы данного образца (решетки). Величину Т1 обычно называют временем спин- решеточной релаксации. В течение этого времени устанавливается разность заселенности уровней, отвечающая данному значению Н0 и температуры. Результатом этой разности является появление результирующего макроскопического магнитного момента образца. Поэтому можно сказать, что Т1 представляет собой время, необходимое для намагничивания образца.

Процесс спин- решеточной релаксации приводит к уширению резонансной линии, т.к. переходы, индуцируемые другими степенями свободы молекулы, делают конечным время жизни ядра в данном состоянии. Порядок величины уширения, вызванного этим процессом, равна:

Dn»p¤2Dt, (2.19)

где Dn [Гц].

В выражении (2.19) Dt – характеристическое время того процесса, который приводит неопределенности в значении резонансной частоты, т.е. обуславливает уширение сигнала. Т.о., ширина линии в единицах частоты, обусловленная спин- решеточной релаксацией, приблизительно равна 1/Т1.

Время спин- решеточной релаксации существенно зависит от окружающей среды и типа ядра. Передача магнитной энергии от протонов и других ядер со спином 1/2 к другим степеням свободы может происходить только одним путем – посредством флуктуаций локальных магнитных полей. Ядра с более высокими значениями спина имеют электрические квадрупольные моменты, которые могут взаимодействовать с флуктуирующими электрическими полями. Поэтому значения Т1 для таких ядер меньше. Для жидкостей значения времен спин- решеточной релаксации лежат в пределах 10-2 – 102 с. в твердых телах Т1 меняется от 10-4 – 104 с.

2.4. Спин- спиновая релаксация.

Кроме взаимодействия с решеткой, ядра могут также взаимодействовать между собой. Этот процесс характеризуется временем спин- спинового взаимодействия, которое обозначается обычно как Т2. На каждый магнитный момент ядра действуют не только постоянное магнитное поле Н0, но и слабое локальное магнитное поле лок, создаваемое магнитными ядрами. Магнитный диполь на расстоянии r создает поле m/r3.

С ростом r напряженность поля лок быстро падает, так что существенное влияние могут оказывать только ближайшие соседние ядра. По этой причине разные ядра оказываются в разных постоянных магнитных полях. Результатом чего должен быть разброс (неопределенность) значений энергетических уровней совокупности резонирующих ядер, т.е. неопределенность частоты резонансных сигналов, и как следствие этого – уширение линий. Изменение ориентации и диффузия молекул в жидкостях, газах и некоторых твердых телах происходят обычно настолько быстро, что локальное магнитное поле усредняется до очень малой величины (104 – 105 раз) по сравнению с лок для жесткой решетки, т.е. при фиксированном относительно друг друга расположении ядер. В соответствии с таким усреднением наблюдаются узкие резонансные линии. По величине разброса локального поля лок с помощью уравнения резонанса можно найти разброс частоты ларморовой прецессии:

Dn=mлок/Iħ. (2.20)

Если в какой- либо момент времени ядерные диполи прецессируют в фазе, то время, необходимое, чтобы фазы прецессии разошлись, равно (Δν)-1. это время можно рассматривать как часть времени Т2.

Существует еще один аспект взаимодействия соседних ядер (магнитных диполей), который также следует учитывать при изучении причин уширения линий. Ядерные спины даже в твердых телах прецессируют вокруг направления внешнего магнитного поля 0. Поэтому создаваемые ими локальные поля можно разложить на статическую компоненту ст (направленную вдоль 0) и осциллирующую осц. Эта компонента создает магнитное поле, которое может индуцировать переходы соседнего ядра, если это ядро прецессирует с той же частотой. В результате ядро j, создающее магнитное поле, осциллирующее с ларморовой частотой, может вызвать переход у ядра i. Энергия для такого процесса берется от ядра j, и происходит одновременная переориентация (переброс) обоих ядер, т.е. обмен энергией при сохранении общей энергии ядер (рис.5.).

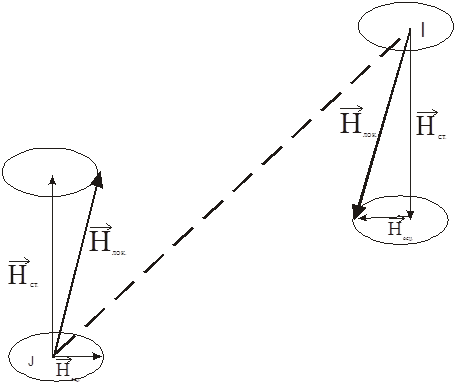
Рис.5. Локальные поля, создаваемые ядерным магнитным диполем.

Однако время жизни каждого из них на данном энергетическом уровне уменьшается. Поскольку относительные фазы ядер изменяются за время (Δν)-1, то для спинового обмена требуется интервал времени такого же порядка. Этот процесс вызывает дальнейшее уменьшение времени Т2, т.е. уширение резонансной линии (наблюдаемое при фиксированной частоте) на величину порядка лок. Оба эти фактора учитываются в величине Т2, которая определяется как время жизни спинов в определенном состоянии и которая представляет собой величину, обратную ширине спектральной линии:

Т2=1/(πΔν). (2.21)

Дипольное уширение и спин- спиновый обмен – это не только лишь два подхода к интерпретации одного итого же явления. В образце, содержащем ядра А и В, не может быть взаимного спин- спинового обмена между данными ядрами, т.к. частоты прецессии сильно различаются. Однако дипольное взаимодействие между ядрами А и В будет наблюдаться, а следовательно, и уширение сигнала.

Следует отметить, что кроме спин- решеточной и спин- спиновой релаксации имеются иные причины уширения линий ЯМР. К этому приводит неоднородность постоянного магнитного поля , т.к. в действительности получается наложение линий поглощения от молекул, находящихся в различных частях образца. На форму линии, а значит и на ее ширину, могут влиять насыщение, нестационарные (переходные) процессы, а также технические характеристики аппаратуры.

2.5. Природа магнитной релаксации.

Для того чтобы механизм релаксации действовал эффективно, необходимо выполнение двух условий. Должно существовать некоторое взаимодействие, которое:

– оказывает непосредственное влияние на спины;

– зависит от времени.

Любое статическое взаимодействие просто влияет на положение и интенсивности спектральных линий, не уширяя их. Существует широкий ряд механизмов релаксации, порождаемых известными типами ядерных взаимодействий в сочетании с каждым из возможных типов движений (степеней свободы). Большинство из механизмов обусловлено следующими причинами:

– диполь- дипольным взаимодействием магнитных ядер между собой;

– флуктуацией локальных полей, обусловленных сильно анизотропным химическим сдвигом в молекуле, совершающей хаотическое движение;

– взаимодействием квадрупольных моментов ядер, имеющих спин больше 1/2, с градиентами электрических полей, изменяющихся во время молекулярного движения;

– мощными магнитными полями, создаваемыми спинами неспаренных электронов парамагнитных примесей в исследуемых образцах.

Релаксационные процессы – обширная и довольно сложная область магнитного резонанса. Теоретическое объяснение каждого из механизмов требует отдельного рассмотрения. Рассмотрим влияние квадрупольного взаимодействия, т.к. данный вид релаксации очень часто оказывает существенное влияние на спектры ЯМР многих веществ.

Ядра со спином, превышающим 1/2 , обычно имеют распределение ядерного заряда, не имеющее сферической симметрии. В результате такие ядра имеют квадрупольный момент Q. Положительный или отрицательный знак Q означает, что заряд распределен относительно оси, совпадающей с направлением спина, в форме вытянутого или сплюснутого эллипсоида вращения. Ядра не обладают электрическим дипольным моментом, и поэтому энергия ядра не зависит от его ориентации в однородном электрическом поле. Однако, при наличии градиента электрического поля квадрупольные моменты прецессируют, что вызывает сдвиг магнитных уровней ядер. Энергия квадрупольного взаимодействия может иметь значения от пренебрежимо малых до значительно превышающих ядерные дипольные магнитные взаимодействия.

Градиент электрического поля может создаваться как самой молекулой (вдоль связи), так и ее окружением в кристалле. Градиенты межмолекулярного электрического поля в жидкостях и газах под действием броуновского движения приближается к нулю. Однако это не относится к внутримолекулярным градиентам в ковалентных связях. Усредненное по времени такое взаимодействие превышает магнитные взаимодействия. Т.о., флуктуации градиентов электрического поля создают эффективный механизм магнитной релаксации. За счет этого время спин- решеточной релаксации может уменьшаться до 10-4 с. Экспериментальное проявление квадрупольного взаимодействия сводится к тому, что оно уширяет резонансные сигналы, а спин- спиновое взаимодействие не проявляется в спектрах ЯМР.

Если ядро, обладающее квадрупольным моментом, находится в достаточно симметричном окружении, то градиент электрического поля в месте нахождения ядра должен быть равен нулю, и, т.о., эффекты квадрупольного взаимодействия исключаются. Это дает возможность наблюдать спектры магнитного резонанса ядер, имеющих значительные квадрупольные моменты, в кристаллах кубической симметрии и в ионных растворах.

Сольватация может искажать сферическую симметрию ионов и вести к уширению линий вследствие появления квадрупольного вклада в Т1.

3.Типы методов ЯМР.

3.1.Спектроскопия ЯМР высокого разрешения.

   Сущность явления ЯМР можно проиллюстрировать следующим образом. Если ядро, обладающее магнитным моментом, помещено в однородное поле 0 , направленное по оси z, то его энергия (по отношению к энергии при отсутствии поля) равна -mzH0, где mz- проекция ядерного магнитного момента на    направление       поля.
   Как уже отмечалось, ядро может находиться в 2I + 1 состояниях. При отсутствии внешнего поля 0 все эти состояния имеют одинаковую энергию. Если обозначить наибольшее измеримое значение компоненты магнитного момента через m, то все измеримые значения компоненты магнитного момента (в данном случае mz) выражаются в виде mm, где m - квантовое число, которое может принимать, как известно, значения
   m=I,I–1,I–2,…,-(I+1),-I.
   Так как расстояние между уровнями энергии, соответствующими каждому из 2I + 1 состояний, равно mH0 / I, то ядро со спином I имеет дискретные уровни    энергии:
-mH0,-(I–1)/ImH0,…(I–1)/ImH0,mH0.
   Расщепление уровней энергии в магнитном поле можно назвать ядерным зеемановским расщеплением, так как оно аналогично расщеплению электронных уровней в магнитном поле (эффект Зеемана). Зеемановское расщепление проиллюстрировано на рис. 6 для системы с I = 1 (с тремя уровнями энергии).

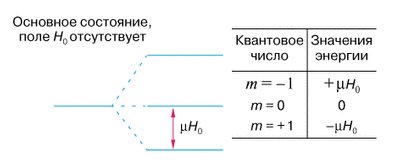
Зеемановское расщепление уровней энергии ядра в магнитном поле

Рис.6. Зеемановское расщепление уровней энергии ядра в магнитном поле.

Явление ЯМР состоит в резонансном поглощении электромагнитной энергии, обусловленном магнетизмом ядер. Отсюда вытекает очевидное название явления: ядерный - речь идет о системе ядер, магнитный - имеются в виду только их магнитные свойства, резонанс - само явление носит резонансный характер. Действительно, из правил частот Бора следует, что частота n электромагнитного поля, вызывающего переходы между соседними уровнями, определяется формулой:

hν=μH0/I, или ν=μH0/hI.
Так как векторы момента количества движения (углового момента) и магнитного момента параллельны, то часто удобно характеризовать магнитные свойства ядер величиной g, определяемой соотношением

m=g(Iħ),
где γ - гиромагнитное отношение, имеющее размерность радиан*эрстед-1*секунда-1 (рад*Э-1*с-1). С учетом этого найдем

ν=γ0/2π.                                                                                                           (3.2)
   Таким образом, частота пропорциональна приложенному полю.
Если в качестве типичного примера взять значение $\gamma$ для протона, равное 2,6753*104 рад/(Э*с), и H0 = 10000 Э, то резонансная частота
ν=42.577    (МГц)
   Такая частота может быть генерирована обычными радиотехническими методами.
   Спектроскопия ЯМР характеризуется рядом особенностей, выделяющих ее среди других аналитических методов. Около половины ( $\sim$ 150) ядер известных изотопов имеют магнитные моменты, однако только меньшая часть          их     систематически          используется.
   До появления спектрометров, работающих в импульсном режиме, большинство исследований выполнялось с использованием явления ЯМР на ядрах водорода (протонах) 1H (протонный магнитный резонанс - ПМР) и фтора 19F. Эти ядра обладают идеальными для спектроскопии ЯМР свойствами:

высокое естественное содержание "магнитного" изотопа (1H 99,98%, 19F 100%); для сравнения можно упомянуть, что естественное содержание "магнитного" изотопа углерода 13C составляет 1,1%;
большой магнитный момент;
спин I = 1/2.

   Это обусловливает прежде всего высокую чувствительность метода при детектировании сигналов от указанных выше ядер. Кроме того, существует теоретически строго обоснованное правило, согласно которому только ядра со спином, равным или большим единицы, обладают электрическим квадрупольным моментом. Следовательно, эксперименты по ЯМР 1H и 19F не осложняются взаимодействием ядерного квадрупольного момента ядра с электрическим      окружением.
   Внедрение импульсных спектрометров ЯМР в повседневную практику существенно расширило экспериментальные возможности этого вида спектроскопии. В частности, запись спектров ЯМР 13C растворов - важнейшего для химии изотопа - теперь является фактически привычной процедурой. Обычным явлением стало также детектирование сигналов от ядер, интенсивность сигналов ЯМР которых во много раз меньше интенсивности для сигналов от 1H, в том числе и в твердой фазе.
   Спектры ЯМР высокого разрешения обычно состоят из узких, хорошо разрешенных линий (сигналов), соответствующих магнитным ядрам в различном химическом окружении. Интенсивности (площади) сигналов при записи спектров пропорциональны числу магнитных ядер в каждой группировке, что дает возможность проводить количественный анализ по спектрам      ЯМР           без    предварительной          калибровки.
   Еще одна особенность ЯМР - влияние обменных процессов, в которых участвуют резонирующие ядра, на положение и ширину резонансных сигналов. Таким образом, по спектрам ЯМР можно изучать природу таких процессов. Линии ЯМР в спектрах жидкостей обычно имеют ширину 0,1 - 1 Гц (ЯМР высокого разрешения), в то время как те же самые ядра, исследуемые в твердой фазе, будут обусловливать появление линий шириной порядка 1*104 Гц (отсюда понятие ЯМР широких линий).
   В спектроскопии ЯМР высокого разрешения имеются два главных источника информации о строении и динамике молекул:

химический сдвиг;
константы спин-спинового взаимодействия.

Химический сдвиг

В реальных условиях резонирующие ядра, сигналы ЯМР которых детектируются, являются составной частью атомов или молекул. При помещении исследуемых веществ в магнитное поле (0) возникает диамагнитный момент атомов (молекул), обусловленный орбитальным движением электронов. Это движение электронов образует эффективные токи и, следовательно, создает вторичное магнитное поле, пропорциональное в соответствии с законом Ленца полю 0 и противоположно направленное. Данное вторичное поле действует на ядро. Таким образом, локальное поле в том месте, где находится резонирующее ядро,

лок=0 (3.3)
где σ- безразмерная постоянная, называемая постоянной экранирования и не зависящая от 0, но сильно зависящая от химического (электронного) окружения; она характеризует уменьшение лок по сравнению с 0 .
Величина $\sigma$ меняется от значения порядка 10-5 для протона до значений порядка 10-2 для тяжелых ядер. С учетом выражения для лок имеем:

ν=γΗ0(1−σ)/2π (3.4)
Эффект экранирования заключается в уменьшении расстояния между уровнями ядерной магнитной энергии или, другими словами, приводит к сближению зеемановских уровней (рис.7). При этом кванты энергии, вызывающие переходы между уровнями, становятся меньше и, следовательно, резонанс наступает при меньших частотах (см. выражение (3.4)). Если проводить эксперимент, изменяя поле 0 до тех пор, пока не наступит резонанс, то напряженность приложенного поля должна иметь большую величину по сравнению со случаем, когда ядро не экранировано.

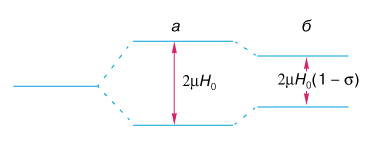
Влияние электронного экранирования на зеемановские уровни ядра: а - неэкранированного, б - экранированного

Рис.7. Влияние электронного экранирования на зеемановские уровни ядра: а - неэкранированного, б - экранированного.

   В подавляющем большинстве спектрометров ЯМР запись спектров осуществляется при изменении поля слева направо, поэтому сигналы (пики) наиболее экранированных ядер должны находиться в правой части спектра.
   Смещение сигнала в зависимости от химического окружения, обусловленное различием в константах экранирования, называется химическим      сдвигом.
   Впервые сообщения об открытии химического сдвига появились в нескольких публикациях 1950 - 1951 годов. Среди них необходимо выделить работу Арнольда, получившего первый спектр с отдельными линиями, соответствующими химически различным положениям одинаковых ядер 1H в одной молекуле. Речь идет об этиловом спирте CH3CH2OH, типичный спектр ЯМР 1H которого при низком разрешении показан на рис. 8.

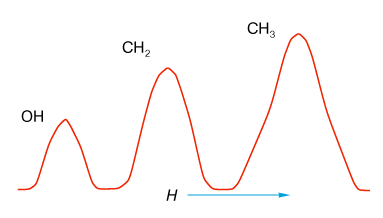
Спектр протонного резонанса жидкого этилового спирта, снятый при низком разрешении

Рис.8. Спектр протонного резонанса жидкого этилового спирта, снятый при низком разрешении.

В этой молекуле три типа протонов: три протона метильной группы CH3-, два протона метиленовой группы -CH2- и один протон гидроксильной группы -OH. Видно, что три отдельных сигнала соответствуют трем типам протонов. Так как интенсивность сигналов находится в соотношении 3 : 2 : 1, то расшифровка спектра (отнесение сигналов) не представляет труда.
Поскольку химические сдвиги нельзя измерять в абсолютной шкале, то есть относительно ядра, лишенного всех его электронов, то в качестве условного нуля используется сигнал эталонного соединения. Обычно значения химического сдвига для любых ядер приводятся в виде безразмерного параметра δ, определяемого следующим образом:

δ=(H−Hэт)/Hэт*106,                                                                                                (3.6)
где (Н - Нэт) - есть разность химических сдвигов для исследуемого образца и эталона, Нэт - абсолютное положение сигнала эталона при приложенном поле (Н0)         .
   В реальных условиях эксперимента более точно можно измерить частоту, а не поле, поэтому $\delta$ обычно находят из выражения:

δ=(ν−νэт)/ν0*106,                                                                                              (3.7)
где (ν – νэт) - есть разность химических сдвигов для образца и эталона, выраженная в единицах частоты (Гц); в этих единицах обычно производится калибровка         спектров          ЯМР.
    Следует пользоваться не ν0 - рабочей частотой спектрометра (она обычно фиксирована), а частотой νэт, то есть абсолютной частотой, на которой наблюдается резонансный сигнал эталона. Однако вносимая при такой замене ошибка очень мала, так как ν0 и νэт почти равны (отличие составляет 10-5, то есть на величину σ для протона). Поскольку разные спектрометры ЯМР работают на разных частотах ν0 (и, следовательно, при различных полях Н0), очевидна необходимость выражения δ в безразмерных единицах.
   За единицу химического сдвига принимается одна миллионная доля напряженности поля или резонансной частоты.

Спин-спиновое взаимодействие

В 1951 - 1953 годах при записи спектров ЯМР ряда жидкостей обнаружилось, что в спектрах некоторых веществ больше линий, чем это следует из простой оценки числа неэквивалентных ядер. Один из первых примеров - это резонанс на фторе в молекуле POCl2F. Спектр 19F состоит из двух линий равной интенсивности, хотя в молекуле есть только один атом фтора (рис. 9). Молекулы других соединений давали симметричные мультиплетные сигналы (триплеты, квартеты и т.д.).

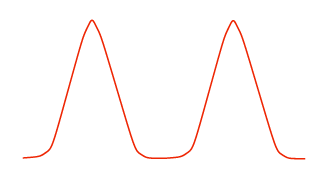
Дублет в спектре резонанса на ядрах фтора

Рис.9. Дублет в спектре резонанса на ядрах фтора в молекуле POCl2F.

Другим важным фактором, обнаруженным в таких спектрах, было то, что расстояние между линиями, измеренное в частотной шкале, не зависит от приложенного поля Н0 , вместо того чтобы быть ему пропорциональным, как должно быть в случае, если бы мультиплетность возникала из-за различия в константах          экранирования.
   Это взаимодействие обусловлено механизмом косвенной связи через электронное окружение. Ядерный спин стремится ориентировать спины электронов, окружающих данное ядро. Те, в свою очередь, ориентируют спины других электронов и через них - спины других ядер. Энергия спин-спинового взаимодействия обычно выражается в герцах (то есть постоянную Планка принимают за единицу энергии, исходя из того, что Е=hν). Ясно, что нет необходимости (в отличие от химического сдвига) выражать ее в относительных единицах, так как обсуждаемое взаимодействие, как отмечалось выше, не зависит от напряженности внешнего поля. Величину взаимодействия можно определить измеряя расстояние между компонентами соответствующего мультиплета.
   Простейшим примером расщепления из-за спин-спиновой связи, с которым можно встретиться, является резонансный спектр молекулы, содержащей два сорта магнитных ядер А и Х. Ядра А и Х могут представлять собой как различные ядра, так и ядра одного изотопа (например, 1H) в том случае, когда химические сдвиги между их резонансными сигналами велики.
На рис. 10 показано, как выглядит спектр ЯМР, если оба ядра, то есть А и Х, имеют спин, равный 1/2. Расстояние между компонентами в каждом дублете называют константой спин-спинового взаимодействия и обычно обозначают как J (Гц); в данном случае это константа JАХ .

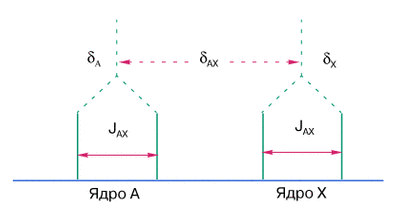
Вид спектра ЯМР системы, состоящей из магнитных ядер А и Х со спином I = 1/2

Рис.10. Вид спектра ЯМР системы, состоящей из магнитных ядер А и Х со спином I = 1/2 при выполнении условия $\delta_{AX} \gg J_{AX}$ .

Возникновение дублетов обусловлено тем, что каждое ядро расщепляет резонансные линии соседнего ядра на 2I + 1 компонент. Разности энергий между различными спиновыми состояниями так малы, что при тепловом равновесии вероятности этих состояний в соответствии с больцмановским распределением оказываются почти равными. Следовательно, интенсивности всех линий мультиплета, получающегося от взаимодействия с одним ядром, будут равны. В случае, когда имеется n эквивалентных ядер (то есть одинаково экранированных, поэтому их сигналы имеют одинаковый химический сдвиг), резонансный сигнал соседнего ядра расщепляется на 2nI + 1 линий.

3.2.Методы спинового эха.

В экспериментах, когда высокочастотное поле 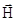1 непрерывно действует на образец, находящийся в однородном магнитном поле 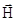0, достигается стационарное состояние, при котором взаимно скомпенсированы две противоположные тенденции. С одной стороны, под действием высокочастотного поля 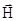1 числа заполнения зеемановских уровней стремятся выравняться, что приводит к размагничиванию системы, а с другой стороны, тепловое движение препятствует этому и восстанавливает больцмановское распределение.

Совершенно иные неустановившиеся процессы наблюдаются в тех случаях, когда высокочастотное поле 1 включается на короткое время. Практическое осуществление экспериментов подобного рода возможно, поскольку характерные временные параметры электронной аппаратуры малы по сравнению с временем затухания ларморовой прецессии Т2.

Впервые реакцию системы на импульсы высокочастотного поля наблюдал Хан в 1950г., открыв явление- спиновое эхо. Это открытие положило начало развитию импульсных методов ЯМР.

Действие поля 1, вращающегося с резонансной частотой, сводится к отклонению намагниченности от первоначального равновесного направления, параллельного полю 0. если поле включают лишь на короткий промежуток времени, а затем опять отключают, то угол отклонения вектора намагниченности зависит от длительности импульса. После включения поля 1 вектор намагниченности будет прецессировать вокруг поля 0 до тех пор, пока его компоненты, перпендикулярные полю 0 , не исчезнут либо за счет релаксации, либо за счет других причин. Индукционный сигнал, который наблюдают после выключения высокочастотного поля 1, представляет собой затухание свободной прецессии, рассмотренное впервые Блохом.

Если напряженность поля 1 велика, а продолжительность импульса tw настолько мала, что в течение действия импульса релаксационными процессами можно пренебречь, то действие поля 1 сведется к повороту вектора намагниченности на угол g1tw (g1-угловая скорость, с которой поле 1 отклоняет вектор от оси z). Если величины 1 и tw выбраны таким образом, что

g1tw=1/2p, (3.8)

то вектор после поворота окажется в плоскости ху. Такие импульсы называют импульсами поворота на 900 (или 900-ные импульсы). Те импульсы, для которых g1tw=p, называются импульсами поворота на 1800 (1800-ные импульсы).

Действие последних импульсов на вектор намагниченности приводит к изменению его первоначального направления на противоположное. Действие 900-ных импульсов можно лучше понять, рассматривая их в системе координат, вращающейся с угловой скоростью, равной частоте поля 1. Если длительность импульса мала, так что окончательный результат мало зависит от величины отклонения частоты поля 1 от резонансного значения, то в такой системе координат вектор намагниченности М сразу после окончания действия импульса будет направлен по оси v.

Если постоянное поле 0 совершенно однородно, то поведение вектора намагниченности после окончания действия импульса определяется только процессами релаксации. Поэтому компонента вектора намагниченности , расположенная в плоскости, перпендикулярной полю 0, будет вращаться вокруг этого направления с ларморовой частотой, в то время как ее амплитуда будет стремиться к нулю по закону exp(-t/T2).

В том случае, когда неоднородность магнитного поля Н0 нельзя пренебречь, затухание происходит быстрее. Это явление можно представить наглядно при помощи ряда диаграмм, показывающих положение вектора на-

магниченности в различных частях образца в определенные моменты процесса затухания. Предположим, что образец разделен на несколько областей, а в пределах каждой области магнитное поле однородно, и намагниченность характеризуется своим вектором i. Наличие неоднородности магнитного поля 0 приведет к тому, что вместо прецессии результирующего вектора намагниченности с определенной ларморовой частотой w0 будет происходить прецессия набора векторов намагниченности с частотами, распределенными по некоторому закону.

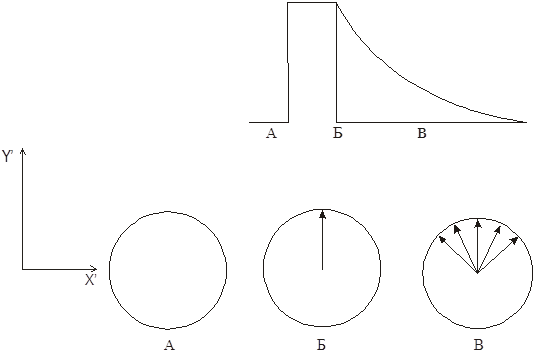
Рис.11. Поведение спиновых изохроматов во время затухания свободной прецессии:

а- в начале импульса; б- в конце импульса; в- во время затухания.

Рассмотрим движение этих векторов в системе координат, вращающейся с угловой скоростью, которая равна средней скорости ларморовой прецессии, соответствующей некоторому среднему значению поля Н0. векторы i называют спиновыми изохроматами.

Действие 900-ного импульса состоит в том, что после его окончания все векторы i оказываются в плоскости xy, перпендикулярной направлению постоянного магнитного поля 0. если выбрать оси х’ и у’ во вращающейся системе координат так, что высокочастотное поле 1 будет направлено по оси х’, то в конце импульса все спиновые изохроматы будут параллельны оси у’ (рис.11б).

Однако ввиду того, что они имеют разные скорости прецессии, т.к. находятся в областях образца с различными значениями поля 0, то некоторые из них будут вращаться быстрее, а некоторые - медленнее системы координат. Поэтому в системе координат, вращающейся с некоторой средней угловой скоростью, спиновые изохроматы будут рассыпаться в “веер”, как это показано на рис.11в. Т.к. приемная катушка индукционной системы реагирует только на векторную сумму этих моментов, то наблюдается затухание сигнала.

Хан нашел, что воздействие на систему второго импульса через промежуток времени τ после первого приводит к появлению через равный промежуток времени 2τ эхо-сигнала. Эхо-сигнал наблюдается даже в том случае, когда за время 2τ произойдет полное затухание сигнала свободной прецессии.

На рис.12. представлен ряд диаграмм, показывающий, как система спиновых изохроматов реагирует на последовательное приложение к ней 900- и 1800-ных импульсов. Последовательные этапы явления, представленные на этих диаграммах (рис.12.), таковы:

1. Первоначально система находится в тепловом равновесии, и все векторы намагниченности параллельны постоянному полю 0.

2. Под влиянием высокочастотного поля, направленного по оси х΄ вращающейся системы координат, векторы намагниченности за время первого импульса отклоняются от направления оси z к направлению оси у΄.

3. После окончания 900-го импульса все векторы намагниченности расположены в экваториальной плоскости в направлении оси у΄ (векторное произведение [1] есть вектор, перпендикулярный в данном случае плоскости z΄x΄). Если продолжительность импульса tω достаточно мала, то никакой релаксации или рассыпания векторов намагниченности в "веер", связанного с неоднородностью поля 0, наблюдаться не будет.

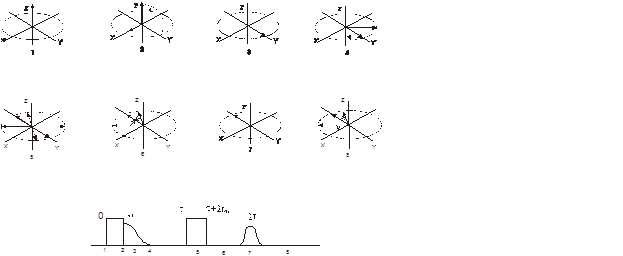
Рис.12. Образование сигнала спинового эха при воздействии 900- и 1800-ных импульсов

4. Сразу же после включения высокочастотного поля Н1 происходит затухание свободной прецессии, что приводит к рассыпанию спиновых изохроматов в "веер", расположенный в плоскости х΄у΄.

5. через промежуток времени τ на систему действует 1800-ный импульс продолжительностью 2tω. В результате действия этого импульса вся система векторов i поворачивается на 1800 вокруг оси х΄.

6. По окончании второго импульса каждый из векторов намагниченности во вращающейся системе координат продолжает двигаться в прежнем направлении. Однако теперь, после поворота на 1800, это движение приводит не к рассыпанию, а к складыванию ″веера″ векторов.

7. Через промежуток времени 2τ после начала первого импульса все векторы намагниченности, находящиеся в плоскости х΄у΄, будут иметь одно и то же направление и создадут сильный результирующий магнитный момент в отрицательном направлении оси у΄. Это приводит к наведению в приемной катушке сигнала, называемого эхо-сигналом.

8. После появления эхо-сигнала векторы намагниченности опять рассыпаются в "веер", и наблюдается обычное затухание свободной прецессии. Затухание сигнала эхо (начиная с момента времени 2τ) совпадает по форме с затуханием сигнала свободной индукции после первого 900-го импульса. Сразу за 1800-ным импульсом никакого сигнала свободной индукции не возникает.

Форма эхо-сигнала, как и форма сигнала затухания свободной прецессии, зависит от временного закона, которому подчиняется рассыпание в "веер" вектора намагниченности. Если магнитное поле неоднородно, то когерентность теряется быстро и эхо-сигнал будет узким ;ширина его порядка (γΔΗ0)-1. Т.о., механизм спинового эха исключает обычное нежелательное влияние неоднородности стационарного магнитного поля.

Если молекулы остаются продолжительное время в одних и тех же частях образца, то амплитуда эхо-сигнала определяется только процессами релаксации и, следовательно, пропорциональна ехр(-2τ/Т2). Однако в жидкостях и газах процессами диффузии можно пренебрегать не всегда. Поэтому, вследствие передвижения молекул в неоднородном магнитном поле, скорость рассыпания в "веер" некоторых векторов намагниченности изменяется.

В результате происходит некоторая дополнительная потеря когерентности. В этом случае амплитуда эхо-сигнала оказывается зависящей от τ следующим образом:

ехр[–2τ/T2 –k(2τ)3/3]. (3.9)

Для эхо-сигналов, полученных для последовательности 900- и 1800-ных импульсов

k=1/4γ2GD , (3.10)

где D – константа диффузии;

G – среднее значение градиента магнитного поля (dH0/dt)ср.

Если выполняется условие

12/γ2G2D<< T32, (3.11)

то главную роль в затухании сигналов спинового эха будут играть процессы диффузии, а не релаксационные процессы. Аналогичные явления наблюдаются и для любых других импульсов, а не только для последовательности 900- и 1800-ных импульсов. Если применяется последовательность 900-ных импульсов, то после второго импульса появляется сигнал затухания свободной прецессии, который отсутствует при применении последовательности 900- и 1800-ных импульсов. Это происходит потому, что по прошествии времени τ, вследствие действия механизма спин-решеточной релаксации, магнитный момент, направленный по оси z, частично восстанавливается. Этот процесс можно охарактеризовать функцией:

f=1 – exp (–τ/T1). (3.12)

Вследствие этого воздействие второго 900-го импульса приводит к сигналу затухания свободной прецессии, амплитуда которого меньше амплитуды первого сигнала в f раз. В том случае, когда вторым импульсом является 1800-ный импульс, этот восстанавливающий магнитный момент будет направлен в отрицательном направлении оси z и, следовательно, проекция его на плоскость ху равна нулю.

Эксперименты по спиновому эху можно проводить с большим числом импульсов. Существуют общие методы расчетов. Пригодные для любой последовательности импульсов.

Если в образце присутствуют ядра с различными резонансными частотами и между ними осуществляется спин-спиновое взаимодействие, то возникают усложнения картины спинового эха. В этом случае зависимость затухания амплитуды сигнала спинового эха от интервала между импульсами τ не подчиняется закону (3.9), а содержит также и некоторые осциллирующие во времени члены. Теперь остановимся на том, как можно управлять фазой переменного напряжения второго импульса так, чтобы во вращающейся системе координат поле 1 было вновь направлено вдоль оси +х΄, как и при первом импульсе. Дело в том, что в, так называемой, когерентной аппаратуре высокостабильный по частоте генератор выдает стационарное переменное напряжение, которое поступает в усилитель мощности через ключевую схему.

Ключевая схема пропускает радиочастотный сигнал (поле 1), и он усиливается лишь в течение промежутка времени, когда эти схемы открываются стробирующим импульсом. Т.о., мощные радиочастотные импульсы на выходе усилителя во времени совпадают со стробирующими импульсами. Выходное напряжение усилителя прикладывается к катушке с образцом, в которой создается радиочастотное поле 1. Если частота генератора ω точно настроена в резонанс, т.е. ω=ω0, то фаза этого поля всегда одна и та же в системе координат, вращающейся с частотой ω0.

4.Спектрометры ЯМР.

Спектрометр ЯМР должен содержать следующие основные элементы: 1) магнит, создающий поляризующее ядерную спин – систему магнитное поле 0; 2) передатчик, создающий зондирующее поле 1; 3) датчик, в котором под воздействием 0 и 1 в образце возникает сигнал ЯМР; 4) приемник, усиливающий этот сигнал; 5) систему регистрации (самописец, магнитная запись, осциллоскоп и т.д.); 6) устройства обработки информации (интегратор, многоканальный накопитель спектров); 7) систему стабилизации резонансных условий; 8) систему термостатирования образца; 9) передатчик, создающий поле 2 для двойных резонансов; 10) систему программирования регистрации ЯМР: для спин - спектрометра – развертку поля 0 или частоты n0 в заданном интервале с необходимой скоростью, требуемой числом реализаций спектра; для импульсных спектрометров – выбор числа, амплитуды и длительностей зондирующих импульсов, времени отслеживания каждой точки и числа точек интерферрограммы, времени повторения интерферрограммы, числа циклов накопления интерферрограммы; 11) системы коррекции магнитного поля. Это схематическое перечисление показывает, что современный ЯМР–спектрометр – сложная измерительная система.

По назначению ЯМР - спектрометры делят на приборы высокого и низкого разрешения. Граница здесь условная, и все чаще характеристики ЯМР - спектрометров высокого и низкого разрешения объединяют в одном универсальном приборе. Типичный прибор низкого разрешения должен иметь магнит, обеспечивающий относительное разрешение порядка 10-6 ч-1, возможность регистрации ЯМР многих магнитных ядер в широком интервале температур, сопряжение с системой обработки данных, гониометр для кристаллофизических измерений.

Для обеспечения высокой чувствительности применяется модуляционный метод наблюдения сигнала: поле 0 (частота n0) модулируется по синусоидальному закону; частота nm и амплитуда Аm выбираются из соображений оптимизации чувствительности и вносимых такой модуляцией искажений сигнала. Поскольку в кристаллах время спин- решеточной релаксации Т1 может достигать нескольких часов, спектрометр низкого разрешения должен обеспечивать регистрацию ЯМР при исключительно малых уровнях радиочастотного поля 1, чтобы избежать насыщения сигнала. Чувствительность модуляционного метода зависит от отношения Аm/d, причем это отношение для слабых сигналов приходится выбирать сравнимым с единицей. Но тогда возникает сильное модуляционное уширение, которое необходимо учитывать при обработке сигналов. Трудности еще более возрастают, если линия ЯМР имеет широкую и узкую компоненты – при однократной записи невозможно правильно передать отношение интенсивностей этих компонент.

В последнее время приобретают все большую популярность импульсные методы регистрации широких линий ЯМР в твердых телах, однако здесь возникают свои трудности. Чтобы одинаковым образом возбудить все переходы в спиновой системе, необходимо применять очень короткие импульсы длительностью tи£1 мкс; это требует мощных источников радиочастотных колебаний. Кроме того, временный отклик спиновой системы для широких линий (Т2~10 мкс) затухает очень быстро; чтобы за несколько микросекунд произвести достаточное число отсчетов, необходим аналого-цифровой преобразователь с быстродействием порядка 0,1 мкс канал.

Большие трудности возникают из-за звона контура в датчике и перегрузки приемника после мощного импульса. Преимуществом импульсной техники является то, что в одном эксперименте могут быть определены все параметры ядерного магнетизма в образце – моменты, форма линии и времена релаксации. По теореме Фурье, большие частоты соответствуют малым временам. Поэтому создаются импульсные методы для анализа явлений, происходящих через ничтожно малое время после окончания импульса. Они повышают точность определения высших моментов линии ЯМР вплоть до n=14.

Для реализации импульсного сужения (высокого разрешения в твердом теле) число импульсных каналов передатчика должно быть не меньше четырех. Мощные импульсы формируются в режиме усиления колебаний, создаваемых точным задающим генератором. Длительность его работы должна быть достаточно велика для реализации требуемой точности настройки частоты и фазы радиочастотного заполнения импульсов. Кроме того, когерентность спектрометра обеспечивает возможность синхронного детектирования по высокой частоте для повышения чувствительности.

Наряду с синхронным детектированием очень широко применяется накопление сигналов с помощью многоканальных накопителей. Стабильность ЯМР - спектрометров обеспечивает долговремен-
ное однозначное соответствие каждого спектрального интервала Dn номеру канала памяти накопителя.

Спектрометры высокого разрешения по способу нахождения условий резонанса разделяются на стационарные и импульсные спектрометры. В стационарных спектрометрах резонанс находится изменением (разверткой) одного из параметров (n или 0) при фиксировании другого. В импульсных спектрометрах при постоянном внешнем поле 0 образец облучают коротким высокочастотным импульсом длительностью t с частотой n, т.е. спектром частот, основная мощность которого находится в полосе n±1/t. В этой полосе возбуждаются все соответствующие переходы ЯМР, дающие отклик- сигнал спада свободной индукции. Фурье- преобразование этого сигнала дает обычный спектр ЯМР.

Спектрометры, работающие в стационарном режиме, состоят из следующих основных узлов:

- магнит, создающий весьма однородное поле;

- датчик сигналов, содержащий исследуемый образец и приемную катушку;

- блок развертки, позволяющий изменять в небольших пределах основное магнитное поле по определенному закону;

- радиочастотный генератор, работающий в метровом диапазоне;

- радиочастотный приемник и усилитель;

- осциллограф и самопишущий потенциометр для наблюдения и регистрации спектров.

Достаточно быстрое вращение образца позволяет эффективно избавиться от влияния градиентов магнитного поля 0. Данное обстоятельство в связи с непрерывным ростом используемых значений 0 ведет к тому, что достигаемое относительное разрешение, измеряемое как отношение DН/0, где DН – наблюдаемая неоднородность магнитного поля, находится в интервале 10-9 – 10-10. Линии, измеряющиеся десятыми и сотыми долями герца, ширина которых определяется длительностью времени релаксации в жидкости (10 – 20 с), приводят к существенной трудности. Следовательно, на однократную реализацию спектра может потребоваться несколько часов. Это предъявляет очень высокие требования к системе стабилизации резонансных условий, которая обычно осуществляется с помощью ЯМР (по дополнительному образцу – внешняя стабилизация либо по одной из линий исследуемого образца – внутренняя стабилизация). Наиболее удачные результаты получаются при сочетании внутренней и внешней стабилизации.