Реферат: Стрела времени и необратимость, возникновение хаоса из порядка и порядока из хаоса как следствие фундаментального детерминизма

Реферат: Стрела времени и необратимость, возникновение хаоса из порядка и порядока из хаоса как следствие фундаментального детерминизма

Косарев А.В., инженер-теплоэнергетик, к.т.н.

Введение

Пригожин И. в [Л-6] пишет: “Можно ли каким-то образом установить связь между столь различными пониманиями времени – временем как движением в динамике, временем, связанным с необратимостью, в термодинамике, временем как историей в биологии и социологии? Ясно, что установление такой связи – задача не из лёгких. И всё же мы живём в единой Вселенной, и, чтобы достичь согласованной картины мира, частью которого мы являемся, нам необходимо изыскать способ, позволяющий переходить от одного описания к другому”. Цель данной статьи попытаться дать единое представление о времени, применимое для всех означенных выше областей, а также показать способ, который позволит не просто переходить от одного описания к другому, а сделать единое описание всех областей классической динамики (динамики Ньютона, термодинамики, теплопередачи, гидродинамики, электродинамики токов, динамики в биологии) исходя из единых исходных постулатов. Выше перечисленные области классической динамики находятся в вопиющем противоречии. Динамика Ньютона и термодинамика уважительно отгородились друг от друга и придерживаются политики невмешательства в область описания другого. Динамика Ньютона описывает системы состоящие из малого числа частиц, элементов, а термодинамика описывает системы из несчётного числа частиц, элементов. Термодинамика же (во всяком случае классическая) и биология фактически исключают друг друга. Эволюция в термодинамике, вытекающая из её исходных постулатов, приводит к равновесному состоянию, что с точки зрения биологии означает конец развития и смерть. Эволюция по Дарвину, принятая биологией и также отвечающая реальному миру, противоречит постулатам термодинамики. Мало общего, если об этом вообще можно говорить, и между динамикой Ньютона и биологией. Необходимо обратить внимание на то, что и классическая статистическая механика применяет математический аппарат теории вероятностей, опираясь на гипотезу молекулярного хаоса (принцип элементарного беспорядка), предложенную Больцманом, и которая аккумулирует в себе нулевой и второй постулаты термодинамики. Конечно, эта гипотеза подтверждена и опытом и приложениями теории, но тем не менее теоретически не обоснована до сих пор. Сложное и запутанное становится понятным, когда во всём этом удаётся увидеть простое и главное. Таким простым, главным и объединяющим для означенной совокупности знаний является эффект вырождения результирующего импульса в многочастичной среде через нецентральное соударение. Наложение этого эффекта на законы динамики Ньютона позволяет построить классическую макро физику исходя из трёх постулатов, которые лежат в основе динамики Ньютона. Это: закон сохранения и превращения энергии; закон сохранения результирующего импульса (момента импульса); корпускулярный характер строения материи, приводящий к нецентральному соударению.

Последний постулат нигде отдельно не выделяется, но фактически также лежит в основе динамики.

Но сначала о времени.

Время в динамике процессов и в эволюции событий

Проблема времени вызывала интерес с глубокой древности. Во всяком случае с античных времён по сегодняшний день исследователи практически всех направлений уделяли понятию времени самое пристальное внимание.

“Время – фундаментальное измерение нашего бытия. … В том виде, как оно входит в фундаментальные законы физики от классической динамики до теории относительности и квантовой физики, время не содержит в себе различия между прошлым и будущим! Для многих физиков ныне это вопрос веры: до тех пор и поскольку речь идёт о фундаментальном уровне описания, “стрелы времени” не существует. Тем не менее во всех явлениях, с которыми нам приходится иметь дело, будь то явления из области макроскопической физики, химии, биологии, геологии, гуманитарных наук, будущее и прошлое играют различные роли. Существование стрелы времени здесь очевидно. Каким образом может возникнуть стрела времени из фундаментальной концептуальной схемы физики? Каким образом она может возникнуть из симметричного по времени мира? Или, быть может, воспринимаемое нами время не более чем иллюзия? Эти вопросы приводят к парадоксу времени – центральной теме нашей книги.” [Л-5].

Как представляется автору данной статьи ни какого парадокса тут нет, а есть путаница между понятием промежуток времени, используемым динамикой и понятием момент времени, используемый эволюционными теориями. Сразу хочу оговориться, несмотря на частое цитирование Пригожина и зачастую в противоречие того, о чём говорю сам, это не означает противоречия с концепцией Пригожина. Напротив, я пытаюсь дать ответы на сформулированные им вопросы, да и указываемые противоречия по большей части сформулированы именно им для обоснования его концепции.

Время в динамике процессов и в эволюции событий – совершенно разные понятия. Именно соединение вместе этих различных понятий и даёт нам стрелу времени или числовую ось времени.

Рассмотрим время в динамике процессов.

Основная задача динамики, диктуемая её основным законом, заключается в описании движения массы под действием силы. Обратим внимание, что всякий процесс связан с движением, с перемещением в пространстве. Движение характеризуется, в числе прочего, скоростью движения и именно для определения величины скорости и введено понятие времени (промежутка времени) в динамике. А вот само понятие времени (промежутка времени) в динамике возникает из сравнения скоростей различных, не зависимых друг от друга, процессов. Примеры:

Пример-1. Рассмотрим два независимых друг от друга процесса – движение автомобиля по дороге и качание маятника. В процессе движения измеряем расстояние пройденное автомобилем с помощью какой-то эталонной меры и число полных периодов качания маятника. Причём замеры обеих величин начинаем и заканчиваем одновременно. Из отношения замеренных величин, каждая из которых определяется скоростью её процесса и возникает время в динамике процессов (промежуток времени). Мы можем сказать, что на одно полное качание маятника приходится столько-то величин эталонных мер расстояния, которыми измеряется пройденный путь. То есть время выступает как кратная величина скоростей сравниваемых процессов. Здесь мы приняли в качестве эталона сравнения скоростей процессов скорость качания маятника. Можно и наоборот. Теперь принимая скорость эталонного процесса как меру промежутка времени (один период качания маятника – одна секунда, например) получаем кратную скорость любого другого сравниваемого с ним процесса. Из сравнения кратных скоростей (по отношению к маятнику) двух движущихся автомобилей мы и определяем соотношение их скоростей.

Конечно, если автомобили начинают и заканчивают движение одновременно, то для сравнения их скоростей вовсе и не нужно маятника, вовсе и не нужно эталонного процесса. Но если автомобили движутся не одновременно, то для сравнения их скоростей без маятника не обойтись.

Пример-2. Вращение Земли вокруг собственной оси (суточное вращение) и вращение Земли вокруг Солнца (годичное вращение). Здесь ситуация совершенно аналогична ситуации первого примера. Пользуясь астрономическими знаниями, определяем число суточных оборотов за один годовой оборот. Принимая скорость вращения вокруг Солнца за эталонную скорость, находим скорость вращения Земли вокруг своей оси как кратную величину по отношению к вращению Земли вокруг Солнца. Причём это стало возможным потому, что оба эти независимых процесса протекают одновременно. Как и в случае одновременного движения двух автомобилей для определения соотношения скоростей процессов здесь можно обойтись без третьего эталонного. А вот ели замеры производить раздельно, то без процесса качания маятника, например, тоже не обойтись.

Время в динамике процессов (промежуток времени) – это просто скорость какого-то процесса выбранного в качестве эталона сравнения. Параметр времени в динамике процессов введён для выявления соотношения скоростей независимых процессов. Самого времени как “нечто самостоятельное” не существует. В этом смысле время в динамике процессов действительно “иллюзия”. Причём чёткого определения времени (промежутка времени) невозможно дать без существования равномерного периодического процесса, с которого начинается сравнение кратных скоростей других процессов. Под равномерностью периодического процесса нужно понимать не равномерность его скорости, а строгую повторяемость его циклов на каждом этапе цикла. Например, маятник имеет скорость движения от нуля в верхних точках траектории до максимума в нижней, но мы имеем в виду под равномерностью скорости процесса то, что в каждом цикле движения всё строго повторяется, все характеристики процесса. Вот почему в качестве эталонных процессов выбирают качание маятника, вращение Земли вокруг своей оси или вокруг Солнца. Причём для более точного измерения вариаций скорости (кратной скорости) какого-либо процесса в качестве эталона необходимо выбирать равномерный периодический процесс с возможно большей собственной скоростью. По этой причине сегодня в качестве эталона времени выбраны атомные или квантовые часы с большой частотой и высокой степенью повторяемости периодов частот процесса излучения.

Рассмотрим время в эволюции событий.

Эволюция изучает события или иначе видоизменения, метаморфозы, бифуркации, т.е. какие-то резкие качественные изменения наблюдаемой системы, объекта и последовательность этих событий. Наблюдая за событиями, мы можем лишь сказать о том какое событие произошло раньше, а какое позже или они произошли одновременно. Причём вне зависимости то того связаны ли события между собой какой-либо причинно следственной зависимостью или нет. Из простого наблюдения за последовательностью событий возникают понятия прошлого, настоящего и будущего, возникает направление событий. Мы можем говорить о последовательности моментов возникновения этих событий. Но все эти понятия сами по себе не имеют никакого отношения к понятию промежутка времени. Причём в отличии от динамики процессов, где в качестве реальности выступают скорости процессов, а промежуток времени это “иллюзия” отражающая соотношение реальных скоростей, в эволюции событий их последовательность и момент наступления самая, что ни на есть реальность. Объединение столь различных понятий как промежуток времени в динамике процессов и моментов времени в эволюции событий в единую числовую ось времени возможно по той причине, что события наступают в результате протекания физических процессов. Пусть имеем наблюдаемую последовательность событий. Между событиями протекают процессы, порождающие эти события. Замеряя скорости этих процессов по скорости эталонного процесса, получаем промежутки времени между отдельными событиями в последовательности. Теперь осталось выбрать за начало отсчёта какое-либо событие (сотворение мира, рождение Христа или основание Рима) и числовая ось времени готова.

Далее происходит абстрагирование от конкретной последовательности событий и моменты времени на числовой оси получаются как числа, суммирующие последовательность промежутков времени эталонного хронометра. А моменты времени конкретных реальных событий привязывают к полученной абстрактной числовой оси времени и тогда мы получаем даты.

Таким образом равномерный периодический процесс лежит в основе понятия времени. Без него даже эволюционная последовательность событий (если только она сама не равномерна как верстовые столбы) не позволит определить время как аналитическое понятие. Именно по отношению к скорости эталонного равномерного периодического процесса и определяются скорости всех других процессов. Если нет такого эталонного процесса или скорости процессов равны, или при описании процессов не учитывают их скорости, то в такой ситуации параметр времени становится не востребованным. Наглядными примерами являются классическая равновесная термодинамика и преобразования Лоренца. В равновесной термодинамике скорости обратимых процессов принимаются бесконечно медленными, то есть с точки зрения численного анализа равными нулю. А если равны нулю скорости процессов, то и нет нужды во времени как таковом. Преобразования Лоренца специально сконструированы для того, чтобы не допустить скорости большие скорости света. Отсюда та же ситуация, при приближении скорости к скорости света и соответственно выравнивании скоростей время останавливается.

Время как и число – это интеллектуальная категория, служащая для количественного описания окружающего мира и не более того. Процессы и события для своего протекания и осуществления не нуждаются во времени как таковом. Им всё равно будет где-либо качаться маятник или нет. Всё определяется соотношением сил и энергий. Время необходимо человеку для анализа количественных соотношений между этими величинами, для анализа и оценки процессов и событий, реально протекающих в природе. Время – категория, введённая человеком для познания действительности. Без человека нет времени, а есть процессы и события. Объективность времени определяется не секундами и веками (т.е. промежутками времени) и не датами (т.е. моментами времени), а скоростями процессов и фактами событий, не зависящих от субъекта. Время – интеллектуальное тождество скоростям процессов и фактам событий.

Теперь нужно ответить на самый главный и интригующий вопрос, касающийся времени – это вопрос об не обратимости времени.

Эффект вырождения результирующего импульса как связующий элемент, обеспечивающий целостность и единство классической динамики

Мы уже отмечали, что события наступают в результате протекания тех или иных процессов. Даже само событие есть какой-то процесс со своей динамикой, со своими энерго превращениями. Поэтому что бы ответить на вопрос о возможности или не возможности обратной цепи событий, обратного хода времени, нужно ответить на вопрос о возможности или невозможности обратного течения процессов. Вопрос обратимости или не обратимости времени – это вопрос обратимости или не обратимости процессов в динамике. Последнее является доминантой исследований Пригожина и его коллег по данному вопросу. Обоснуем и докажем правильность этой доминанты.

Сначала о обратимости процессов в динамике Ньютона, динамике малого, счётного числа взаимодействующих частиц.

Рассмотрим один из наиболее ярких примеров обратимости процессов в динамике Ньютона – это обратимость движения математического маятника. При качании маятника в ту или иную сторону движения строго повторяются и при описании движения время можно принимать как со знаком плюс так и со знаком минус. Ни сточки зрения количества, ни с точки зрения качества оба описания не будут противоречить друг другу. Качание в одну сторону строго противоположно, обратимо качанию в другую сторону. Усложним ситуацию. Рассмотрим цепочку подвешенных на прямой линии достаточно близко друг к другу совершенно одинаковых математических маятников. Отклоним первый маятник, то есть за счёт совершения работы передадим ему потенциальную энергию, и отпустим. Взаимодействие будем описывать законами центрального абсолютно упругого удара. В системе начнётся процесс последовательного соударения и в цепочке возникнет процесс передачи импульса и энергии вдоль цепочки. При этом каждый акт взаимодействия между массами двух маятников сопровождается переходом кинетической энергии в потенциальную и наоборот и совершается работа против силы или силой. Этот процесс будет протекать до последнего маятника. После того как последний маятник отклонится и энергия системы сосредоточится в потенциальной энергии последнего маятника, весь процесс повторится, но в обратной последовательности, в обратном направлении. Мы растянули процесс во времени, но он остался обратимым. Однако если цепочку маятников предположить бесконечной длины, то процесс передачи импульса и энергии по цепочке станет необратимым. Таким образом теоретически необратимость процесса возможна и в классической динамике Ньютона, но это не локализованная в пространстве и времени, гипотетическая необратимость.

Теперь о необратимости процессов в термодинамике, динамике большого, несчётного числа частиц, которые как показывает практика локализованы и во времени и в пространстве.

Исторически сложилось так, что при рассмотрении процессов в неравновесных термодинамических системах в тени остаётся один из самых фундаментальных законов природы – закон сохранения результирующего импульса как системный закон. Похоже сознание исследователей, воспитанных на трёх законах Ньютона, с аккумулированных в законе сохранения результирующего импульса, было шокировано фактом существования равновесного состояния и неизбежности его наступления. Это привело к отгораживанию динамики Ньютона от термодинамики и в последующем независимому развитию обеих наук. В основу термодинамики был положен факт существования равновесного состояния в тепловых системах и неизбежности его наступления. Были сформулированы нулевой и второй постулаты, которые напрочь отметали закон сохранения результирующего импульса. Термодинамика как бы пренебрегала динамикой Ньютона, претендовавшей на место первой из наук. Видимо это и стало причиной жестокой травли Больцмана со стороны приверженцев классической динамики, когда Больцман делал попытки вывести гипотезу молекулярного хаоса, постулирующую равновесное состояние, из законов классической динамики. А ведь Больцман был так близок к решению этой задачи в своём первом механическом варианте H-теоремы.

На основе последовательного применения к термодинамическим системам (системам состоящим из несчётного числа частиц) закона сохранения результирующего импульса покажем единство динамики малого числа частиц (динамики Ньютона) и динамики несчётного числа частиц (термодинамики). Рассмотрим процессы возникновения кооперативных векторных потоков энергии в неравновесных многочастичных системах и условия, при которых происходит или их затухание, вплоть до равновесного состояния, или формирование диссипативных структур Пригожина.

В учении о тепле факт равновесного состояния и неизбежности его наступления для замкнутой многомолекулярной системы имеет особое, основополагающее значение. Все фундаментальные выводы термодинамики и статистической физики построены на этом факте.

Рассмотрим это наиболее общее свойство всех многомолекулярных систем, т.е. их стремление к равновесию, постараемся раскрыть механизм релаксации подобных систем. Известно, что это свойство обусловлено столкновением частиц между собой и со стенками сосуда. Так вот, возникает вопрос, а как в процессе столкновения частиц между собой и со стенками сосуда направленное движение приходит в равновесное состояние, т.е. каким образом кинетическая энергия направленного движения (кооперативная энергия общего движения частиц) переходит в кинетическую энергию хаотически движущихся частиц?

На первый взгляд покажется вполне понятным и естественным, что если одна или несколько направленно движущихся частиц высокой энергии сталкиваются с большой массой хаотически движущихся частиц, то в результате сталкивания направленные частицы перемешиваются и их направленная энергия будет рассеяна. Однако при таком подходе происходит подмена сложного на хаотическое. При ближайшем рассмотрении выясняется четкий, имеющий свои границы, механизм релаксации, механизм установления равновесия, вытекающий из законов механики.

Во первых покажем что результирующий импульс всех частиц системы, находящейся в равновесии, равен нулю как вектор.

где n-количество частиц в системе.

Обоснование данного утверждения легко провести с помощью выводов статистической физики. Известно, что в случае равновесного состояния в газе всегда реализуется Максвеловское распределение по скоростям. В статистической физике показывается, что для случая Максвеловского распределения по скоростям средняя проекция скорости хаотического движения на любое направление оказывается равной нулю. А если равна нулю проекция средней скорости, то равна нулю и проекция среднего импульса на любое направление. И результирующий импульс равен нулю как вектор.

Теперь рассмотрим замкнутую систему из 10-и частиц, находящихся в покое (для простоты будем рассматривать механическую модель газа - абсолютно упругие шары). Этой замкнутой системе извне передадим импульс . Наиболее характерным свойством этой замкнутой системы, с точки зрения динамики, будет, наряду с сохранением полной энергии то, что этот импульс будет сохраняться постоянным по величине и направлению, сколько бы частицы не сталкивались между собой. При рассмотрении замкнутой системы из 20, 100 частиц свойство сохраняется. Теперь же рассмотрим замкнутую систему из многих и многих миллиардов частиц. Здесь положение коренным образом меняется. Наиболее характерным свойством этой системы является стремление к равновесию, при котором как было показано выше результирующий импульс всех молекул равен нулю как вектор, т.е. направленное движение перейдет в хаотическое. Таким образом с одной стороны для замкнутой механической системы имеем с другой, при увеличении числа частиц системы, имеем прямо противоположное свойство , направленное движение исчезает. Попытаемся выяснить, каким образом разрешается этот парадокс, т.е. рассмотрим механизм релаксации. Каким образом кооперативная кинетическая энергия направленного движения с переходит в кинетическую энергию хаотически движущихся частиц с как вектор? Взаимодействие молекул (шаров) будем описывать законами абсолютно-упругого удара. Так как молекулы имеют конечные размеры, то удар будет нецентральный. Обратим на это особое внимание. Это ключ к решению поставленной задачи. Вероятность центрального удара, согласно положениям статистической физики в системе свободных частиц стремится к нулю. Если не нравятся абсолютно-упругие шары будем понимать под ними силовые поля, имеющие форму шара или круговые эффективные сечения взаимодействия. Причём шаровые силовые поля рассматриваем для упрощения модели, что бы заострить внимание на главном виновнике рассеяния кооперативной энергии – нецентральном соударении.

Пусть имеем замкнутую систему, состоящую из одинаковых шаров. Причем n шаров покоятся, а один шар движется и сталкивается с покоящимися шарами. До столкновения результирующий импульс системы: , т.е. равен импульсу движущегося шара, а кинетическая энергия равна кинетической энергии движущегося шара. Причем кинетическая энергия строго направлена по результирующему импульсу системы, вся переносима этим результирующим импульсом.

Шар 1 (см. рис.1) сталкивается с покоящимися шарами, причем должны при этом выполняться закон сохранения результирующего импульса и закон сохранения кинетической энергии. Пишу закон сохранения кинетической, а не полной энергии, т.к. принято считать что при абсолютно-упругом соударении шаров потенциальная энергия проявляется только в момент непосредственного соприкосновения. Эта схема принимается мною с тем что бы в наибольшей простоте раскрыть механизм рассеяния кооперативной кинетической энергии. При рассмотрении последовательности столкновений будем следить не за траекториями отдельных частиц, которые экспоненциально разбегаются, а за поведением результирующего импульса.

Шар 1 с импульсом после столкновения с первым шаром 2 будет иметь импульс , а шар 2 приобретет импульс которые в сумме (геометрической) дадут первоначальный импульс . Закон сохранения импульса соблюден. Разложим импульсы шаров 1 и 2 после столкновения на оси и . Проекции и дадут в сумме первоначальный импульс , а проекции , перпендикулярные первоначальному результирующему импульсу на его величину после столкновения не влияют и в сумме дают нуль-вектор. Равенство по абсолютной величине импульсов и легко видно из векторной диаграммы и вытекает из закона сохранения результирующего импульса. Однако эти два последних уравновешенных импульса (нуль-вектор) несут каждый на себе определенное количество кинетической энергии, полученной от кинетической энергии первоначального импульса .

Так как и

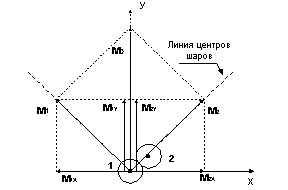
Массы шаров для простоты все равны. Если, как было показано выше, результирующий импульс после столкновения сложится из двух проекций на ось и остался постоянным, то кинетическая энергия, переносимая этим импульсом после столкновения, т.е. проекциями и будет составлять только часть кинетической энергии, переносимой результирующим импульсом до столкновения. Другая часть кинетической энергии, переносимая взаимно уравновешенными импульсами и (нуль-вектором) переходит в хаотическую форму. После следующего соударения теперь уже двух движущихся шаров результирующий импульс сложится из 4-х шаров и произойдет дополнительное рассеяние направленной кинетической энергии и т.д. Таким образом благодаря нецентральному соударению шаров в первоначальный направленный импульс лавинообразно вовлекается все большее и большее число шаров и происходит лавинообразный рост массы результирующего импульса. А по мере вовлечения шаров происходит все большее рассеяние первоначально направленной кинетической энергии. Это видно и из таких простых математических преобразований:

; ;

; m-масса шара ; ; (1)

Так как в результате столкновений в перенос результирующего импульса вовлекается все большее число молекул, то масса результирующего импульса постоянно растет, а скорость результирующего импульса, т.е. общего переноса падает. После рассмотренного соударения масса результирующего импульса возросла вдвое, а скорость уменьшилась вдвое.

Но в кинетическую энергию скорость входит в квадрате, поэтому при увеличении массы в два раза и уменьшении в два раза скорости общего переноса кинетическая энергия общего переноса, т.е. та, которую несет результирующий импульс, уменьшилась вдвое.

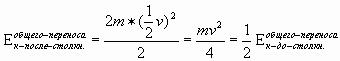
Речь идет о кинетической энергии общего переноса (кооперативной энергии), связанной с результирующим импульсом, т.е. той энергии, которая совершает макроскопическую работу. Закон сохранения общей кинетической энергии системы не нарушается, т.к. адекватно увеличивается хаотическая составляющая кинетической энергии. При увеличении массы, переносящей результирующий импульс, в 10 раз кинетическая энергия, переносимая этим импульсом, и остающаяся в направленной форме, уменьшается в 10 раз. И при стремлении массы результирующего импульса к бесконечности кинетическая энергия общего переноса стремится к нулю. Таким образом при стремлении массы результирующего импульса к бесконечности, т.е. вовлечении в процесс переноса импульса огромного числа частиц, скорость результирующего импульса стремится к нулю и направленное движение затухает. Результирующий импульс, оставаясь постоянным по величине и направлению, вырождается как носитель кооперативной энергии, равносильно тому, что и система приходит в равновесное состояние. Вся кооперативная энергия переходит к нуль-вектору хаоса.

Этим разрешается парадокс который мы выявили в начале. В случае центрального удара рассеяние вообще не происходит. В этом примере мы рассматривали столкновение шара с покоящимися шарами. Картина рассеяния и затухания не изменится, если шары будут не покоиться, а хаотически двигаться с , т.к. причиной рассеяния является не состояние системы, а нецентральное соударение.

Теперь о самом главном – о применении закона сохранения результирующего импульса к многочастичным (термодинамическим) системам. Когда я рассматриваю механизм релаксации термодинамических систем через рассеяние направленной кинетической энергии, переносимой результирующим импульсом, то для замкнутой системы неукоснительно соблюдаю закон сохранения результирующего импульса. Если выше я пишу: “Каким образом кинетическая энергия направленного движения с переходит в кинетическую энергию хаотически движущихся частиц с как вектор”, то это относится не к утверждению, а к постановке задачи. Это утверждение давным давно сделал Клаузиус, когда сформулировал второй закон в форме, что направленный процесс в замкнутой термодинамической системе неизбежно приходит в равновесное состояние. Ведь если процесс направленный, то это кооперативное (совместное) движение многих частиц, а значит имеется результирующий импульс, который должен в замкнутой системе оставаться постоянным как вектор что бы не происходило. Но если система придет в равновесное состояние, т.е. реализуется Максвеловское распределение по скоростям, то легко показывается что в системе Вот это и породило сомнение, появилась необходимость согласовать эти противоречащие друг другу фундаментальные опытные факты. Причём предпочтение отдано закону сохранения результирующего импульса как более фундаментальному закону на том основании что закон сохранения результирующего импульса сформулирован для любых замкнутых систем, а 2-й закон сформулирован только для многочастичных термодинамических замкнутых систем. Однако применяя закон сохранения импульса к диссипативным системам необходимо учитывать одну тонкость, которая и позволяет снять ранее отмеченное противоречие и примирить 2-й закон и закон сохранения результирующего импульса. Эта тонкость является важным свойством диссипативных (термодинамических) систем. Под скоростью центра масс результирующего импульса (см. формулу (1)) нужно понимать не скорость центра масс всей замкнутой системы, которой передан импульс, а скорость центра масс частиц вовлечённых в результате не центрального соударения в перенос первоначального импульса (который относился к первоначальному шару). Это открытая система, активно взаимодействующая с остальной несоизмеримо большей частью всей замкнутой системы и вовлекающая в первоначальный импульс всё большее число молекул через не центральное соударение. Учитывая число частиц реальных термодинамических систем (достаточно вспомнить порядок числа Лошмидта), понятно что в доли времени и на минимальных расстояниях первоначальная масса частиц из которых складывался импульс возрастает в миллиарды и миллиарды раз. Хотя будет составлять малую часть всей замкнутой системы. И далее я показываю, рассматривая механизм релаксации, что кооперативная кинетическая энергия связанная с этим импульсом убывает обратно пропорционально росту массы. Кооперативная энергия разносится взаимно уравновешенными импульсами (см. рис.-1) и направленная кооперативная кинетическая энергия переходит в тепловую форму с . Хотя первоначальный импульс остался постоянным по величине и направлению как вектор ( сложившись из огромного числа микро импульсов вовлеченных частиц), он вырождается как носитель кооперативной энергии, которая перешла к нуль вектору, складывающемуся из пар взаимно уравновешенных импульсов. Даже если будут сталкиваться одновременно три и более частиц (вероятность чего пренебрежимо мала), то и тогда импульсы, разносящие кооперативную энергию перпендикулярно первоначальному импульсу, в сумме должны дать нуль вектор. Иначе будет нарушен закон сохранения результирующего импульса. Так как скорость центра масс открытой системы стремится к нулю (), то я и утверждаю, что с продолжающимся лавинообразным нарастанием массы открытой системы с некоторого момента следующий миллиметр пути импульс не преодолеет никогда, а это значит что перенос кооперативной энергии прекратится. Оставаясь постоянным по величине и направлению как вектор, импульса не стало как энергетического носителя кооперативной энергии. Вот что я понимаю под вырождением результирующего импульса. Он остался постоянным по величине и направлению, но без энергии. Вся его первоначальная энергия перешла к нуль вектору хаоса. Именно это я имею в виду когда пишу . И если ещё учесть что кооперативная энергия не только уменьшается обратно пропорционально суммарной массе вовлеченных в первоначальный импульс частиц, но в процессе развития экспоненциально расширяется и площадь проходного сечения потока кооперативной энергии, то плотность потока энергии (вектор Умова-Пойтинга) убывает ещё быстрее и польза от этой кооперативной энергии с точки зрения совершения полезной работы против сил убывает быстрее убыли её величины. Это и есть механизм релаксации через диссипацию кооперативной энергии, через вырождение результирующего импульса при не центральном соударении.

Теперь рассмотрим другой пример рассеяния направленной кинетической энергии, исключающий соударение шаров (молекул) между собой. Пусть имеем адиабатную полость с отверстием. В отверстие полости влетает n шаров, причем скорости шаров строго параллельны (молекулярный пучок). После того как шары влетают в полость, отверстие за ними закрывается. Рассмотрим как будут развиваться события в этой замкнутой системе. Эта задача решается в теории бильярдов Синая. В начале результирующий импульс равен скалярной сумме всех импульсов шаров, т.к. импульсы шаров параллельны и вся кинетическая энергия переносима результирующим импульсом, находится в кооперативной форме. В следствие того что шары не зависимы друг от друга, то после соударения со стенкой они разлетаются в различных направлениях в зависимости от углов соударения каждого шара со стенкой, а так как стенка имеет кривизну, то углы различны. Строго говоря и здесь нужно вести речь не о кривизне, а о нецентральном соударении по причине корпускулярного строения стенки. Налетающая частица сталкивается со стенкой представляющей для этой частицы потенциальный барьер из суперпозиции силовых полей частиц стенки. Соударение происходит с какой-то отдельной частицей стенки по законам не центрального соударения как и в случае газа. Только частицу в стенке нужно принимать практически бесконечно большой массы, из-за её жестких связей с огромной совокупностью частиц стенки, с которыми она выступает как единое целое. После отражения от стенки результирующий импульс шаров уменьшается, т.к. скорости шаров уже не параллельны. И кинетическая энергия, переносимая результирующим импульсом, соответственно уменьшается. То есть и здесь вырождение импульса, диссипация кооперативной энергии вызывается не центральным соударением и большой массой. И если шаров в пучке много, то после серии столкновений со стенками результирующий импульс будет стремиться к нулю. Здесь стенка изменяет геометрию каждого отдельного импульса, в результате уменьшается результирующий и уменьшается кинетическая энергия общего переноса. Этим и определяется рассеяние кооперативной энергии в ситуации рассматриваемой в теории бильярдов Синая.

Всесилие механизма релаксации, приводящего систему к равновесию, заключается в том, что материя имеет корпускулярное строение, т.е. частицы имеют конечные размеры, а значит соударение нецентральное. Частиц же великое множество и затухание происходит очень быстро. Механизм диссипации направленной энергии через вырождение результирующего импульса имеет универсальный характер не зависимо от среды (газ, жидкость, твердое тело или их совокупность). Именно благодаря этому простому, но всесильному механизму обратимые законы механики в приложении к многомолекулярным системам, вырождаются в необратимые законы статистики. Ведь для обращения процесса релаксации назад необходимо, чтобы в один и тот же момент все частицы системы, вовлеченные так или иначе в процесс релаксации, да и не только они, столкнулись по закону центрального абсолютно-упругого удара с каким-то препятствием, чтобы отлететь с той же скоростью в строго обратном направлении. Это невозможно в принципе. Во - первых в реальности не возможен абсолютно-упругий удар. Во - вторых как в многомолекулярной системе вообще организовать внедрение этих очень массивных, теоретически с бесконечной массой, препятствий? Причём бесконечные массы перед каждой из частиц нужно внедрить мгновенно, в один момент времени, и при этом обеспечить строго центральное соударение, чтобы все частицы одновременно повернуть назад. Кто знает, как это сделать, учитывая порядок числа Лошмидта и то, что реальные частицы не шары? Сказанное и является основой необратимости процесса вырождения импульса в термодинамических макро системах. Релаксация и необратимость вытекают из обратимых законов механики при их действии в среде многомолекулярных систем. Обратим особое внимание на это свойство диссипативных сред, их способность качественно вырождать закон сохранения результирующего импульса и как следствие качественно изменять динамику, когда детерминизм динамики уступает место вероятности статистической механики. Это происходит в результате действия эффекта вырождения результирующего импульса, который является стержневым свойством много частичных (диссипативных) сред. Механизм вырождения результирующего импульса как носителя связанной с ним кооперативной кинетической энергии – самое главное в моей работе. Без этого механизма всё остальное не имеет логического базиса. Остается только удивляться что в так долго длившейся борьбе между двумя подходами к проблеме неравновесности, представителями которых были скажем А. Пуанкаре и Л. Больцман, ускользнул этот объединяющий обе точки зрения момент. Связано это видимо было с тем, что в термодинамике закон сохранения импульса как системный закон всегда был в тени. Его прослеживают только в молекулярно-кинетической теории при каждом акте соударения, не прослеживая его системный характер. Хотя как уже отмечалось выше Больцман в своём первом, механическом варианте H-теоремы был очень близок к решению задачи аналитического доказательства второго закона термодинамики и вывода равновесного состояния из законов динамики. Его ошибкой было принятие модели частиц как материальных точек, что приводило к центральному соударению при рассмотрении столкновений частиц. При центральном соударении рассеяния не происходит в принципе. Причина рассеяния в нецентральном соударении. Вызывают удивление многочисленные возражения механицистов против механического варианта H-теоремы Больцмана. Например возражение высказанное Лошмидтом и известное как “парадокс Лошмидта”. Лошмидт предложил при достижении системой равновесного состояния изменить направления всех молекул на прямо противоположные и тогда система вернётся в исходное неравновесное состояние. Странно, но вместо того, чтобы спросить, а как это сделать хотя бы теоретически, Больцман соглашается с возражением и отказывается от динамического обоснования второго закона.

Особенность нецентрального соударения такова что оно не только способно диссипировать направленную энергию (вырождать ,но благодаря нецентральному соударению возникают хвосты из быстрых частиц в распределении Максвелла по скоростям в равновесном состоянии. Именно благодаря нецентральному соударению появляется вероятность того что много медленных частиц могут разогнать одну до очень больших скоростей. Это хорошо видно на такой простой модели. Если быструю частицу перпендикулярно её скорости ударит в нужный момент медленная частица и передаст ей свой малый импульс, то импульс быстрой частицы, векторно сложившись с полученным малым, дополнительно увеличится. Уменьшающаяся вероятность подобного последовательного воздействия медленных частиц на быструю может разогнать её до очень больших скоростей. К самоорганизации (синергетике) этот процесс не имеет ни какого отношения, он имеет отношение к механическому обоснованию теории флуктуаций. Этим примером я хотел подчеркнуть особое значение для диссипативной среды не центрального соударения, которое не только рассеивает кооперативное движение частиц в хаотическую форму, но и хаотическая форма кинетической энергии в диссипативной среде подвергается рамочному воздействию (в виде Максвеловского распределения по скоростям) не центрального удара.

Таким образом при диссипации направленная кооперативная энергия с вырождается и приходит в состояние когда фактически . Я подчеркиваю фактически, имея ввиду что результирующий импульс уже не несет направленной кинетической энергии. Хотя теоретически он остался постоянным по величине и по направлению. Система приходит в равновесие, энтропия достигает максимума:

и ;

В условиях полного порядка, когда все частицы летят в одном направлении с одинаковыми скоростями (молекулярный пучок):

и ;

В общем случае полная энергия диссипативной системы состоит из двух подсистем: подсистемы порядка с и подсистемы хаоса с .

В системе предоставленной самой себе, в следствие эффекта вырождения импульса, подвергается диссипации и уменьшается направленная доля полной энергии с и , (подсистема направленной энергии в общей системе), а диссипированная часть полной энергии с и увеличивается (подсистема хаоса).

Из изложенного следует что результирующий импульс системы и энтропия системы величины взаимозависимые и находятся в обратной зависимости: если в результате действия причин и механизма релаксации диссипирует и снижается доля направленной энергии (подсистемы порядка с ), то по закону сохранения энергии увеличивается доля хаотической тепловой энергии (подсистемы хаоса с ) и энтропия системы растет, достигая максимума при полном вырождении результирующего импульса, при полной диссипации направленной энергии. Законы сохранения результирующего импульса и роста энтропии замкнутых диссипативных систем нужно рассматривать в единстве, их поведение результат единого развития событий. Закон роста энтропии есть следствие эффекта вырождения результирующего импульса в диссипативной среде, своеобразное выражение закона сохранения импульса в применении к специфичности многомолекулярных диссипативных систем. И учитывая механизм диссипации можно сделать вывод, что 2-й закон термодинамики есть следствие вытекающее из закона сохранения результирующего импульса при его действии в многочастичной диссипативной среде.

Я ни в коем случае не отрицаю второй закон термодинамики, а напротив пытаюсь обосновать причины его всесилия, механизм его реализации, границы его применимости, условия необходимые для его реализации. Я показываю на глубинную связь между вторым законом термодинамики и законом сохранения результирующего импульса, на первичность закона сохранения результирующего импульса и вторичность 2-го закона термодинамики. В динамике малого количества частиц механизм вырождения импульса не заметен, он проявляется только при большом количестве частиц. Обычно никто не возражает что 2-ой закон термодинамики не действует в среде из малого числа частиц, это кажется само собой разумеющимся. Но это не так. Рассеяние происходит и при малом числе соударений, но возможностей такой системы для полного вырождения импульса не хватает. Отметим что эффект вырождения результирующего импульса в много частичной среде является обоснованием гипотезы молекулярного хаоса (принципа элементарного беспорядка), на базисе которой построена статистическая механика.

Необходимо также отметить что эффект вырождения результирующего импульса проявляется в многочастичных средах не только в области классической динамики, но и в квантовой и релятивистской динамике, т.к. нецентральное соударение имеет место во всех областях физической реальности.

Теперь наряду с процессом рассеяния направленной энергии в диссипативной среде рассмотрим противоположный ему процесс самоорганизации хаоса, возникновения диссипативных структур. В этом процессе диссипативная среда с , т.е. не имеющая выраженного направления движения, проходит стадию выравнивания в результате которой возникает диссипативная структура, обладающая кооперативным движением, движением общего переноса с , а стало быть возникает энергия общего переноса способная совершать полезную работу. Вообще в диссипативной (много частичной) среде формируются два типа структур: в литературе они называются статические структуры и динамические структуры. Примером статических структур могут служить кристаллы, агрегаты дипольных молекул жидкостей или химические соединения, в том числе очень сложные, например белки. Эти структуры изучает физическая химия. Здесь мы рассматриваем условия и механизмы самоорганизации в много частичной среде динамических структур, потоков массы и энергии (гидродинамический поток, электрический ток, фононный тепловой поток, фотонный поток лазера).

Согласно положений нелинейной неравновесной термодинамики, необходимым условием самоорганизации открытых диссипативных систем является наличие сильной неравновесности в таких системах.

Во-первых отметим что говоря об открытых системах мы должны оговаривать условие их закрытости в совокупности с какими-либо окружающими телами (окружающей средой) или оговаривать условие энергообмена с ними. В противном случае при анализе таких систем невозможно применять законы сохранения энергии, сохранения результирующего импульса и закон энтропии, сформулированные для замкнутых систем.

Всякая неравновесность состояния термодинамической системы вызвана какой-либо разностью потенциалов (разность давлений, температур, разность химических потенциалов, разность энергетических уровней). Уже в разности потенциалов, в наличии потенциальной энергии и заложена самоорганизация, заложены условия возникновения кооперативного движения. Если в термодинамической системе есть неравновесность, т.е. разность потенциалов, то в этой системе имеется градиент потенциальной энергии. Если в системе есть градиент потенциальной энергии, то в этой системе действует сила, имеющая выделенное направление, против градиента потенциальной энергии:

где - потенциальная энергия, запасенная в системе, ; F - сила, действующая в системе; r - расстояние на котором имеется разность потенциалов .

В этом природа термодинамических сил в многочастичной среде. Она едина с природой любых сил, рассматриваемых в любых средах и всех во областях физики. Далее если в динамической системе (в системе где частицы имеют возможность перемещаться) действует сила, то она вызывает ускоренное движение массы в соответствии с основным законом динамики, (). Так как разность потенциалов действует на всю много частичную систему, то и сила действует на систему в целом, вызывая коллективное совместное движение частиц диссипативной системы. В форме массового (гидродинамического) потока, когда частицы свободны (газ, жидкость) или в форме фононного потока, потока бегущих волн, когда частицы связаны (кристалл) и могут совершать только колебательные движения. Возникают термодинамические потоки массы и энергии, потоки энергии Умова-Пойтинга. Осуществляется переход потенциальной энергии, запасенной в неравновесной системе, в кинетическую энергию общего переноса, имеющей результирующий импульс по направлению силы (-grad).

Это и есть механизм самоорганизации (синергетики) диссипативных структур, основополагающего понятия сильно неравновесной термодинамики. Потенциальная энергия, являющаяся источником неравновесности, не может быть ни направленной, ни хаотической, это энергия положения частиц системы. У потенциальной энергии нет результирующего импульса, но потенциальная энергия может преобразовываться в кинетическую. А вот когда идет преобразование потенциальной энергии (разности потенциалов, неравновесности) в кинетическую энергию, то здесь возникает кинетическая энергия общего переноса по направлению общего градиента потенциальной энергии, (газовый поток при разности давлений, тепловой поток через теплопроводную стенку или в термопаре при разности температур, электрический ток при химической разности потенциалов в аккумуляторной батарее) с и тогда говорим о самоорганизации или кинетическая энергия выделяется с , т.е. в хаотической форме при химических реакциях горения, когда нет общего, выделенного направления, т.к. нет общего градиента потенциальной энергии.

Таким образом самоорганизация диссипативных структур проявляется в возникновении термодинамических потоков массы и энергии, потоков Умова-Пойтинга, имеющих результирующий импульс отличный от нуля. Потоки же возникают под действием сил, порождаемых градиентом потенциальной энергии термодинамической системы в следствии ее неравновесного состояния.

Более ста лет назад профессором Умовым было введено понятие потоков энергии в диссипативной среде, даны их характеристики. Здесь ставится задача выявить механизмы, динамику возникновения потоков энергии в многочастичной среде, понять условия существования этих потоков во времени, причины затухания, рассеяния этих потоков в диссипативной среде. При этом я пытаюсь указать на тесную связь между потоками энергии Умова-Пойтинга в диссипативной среде и диссипативными структурами, введёнными Пригожиным.

Принято считать что “физическая природа синергетики состоит в том что в нелинейной области, вдали от равновесного состояния, система теряет устойчивость и малые флуктуации приводят к новому режиму – совокупному движению многих частиц”.[Л-1]. Это не так. Здесь действует детерменизм, а не вероятность. Механизм возникновения кооперативного движения в неравновесной диссипативной среде не несёт в себе ничего нового по сравнению со вторым, основным законом динамики Ньютона. Просто нужно иметь в виду что сила действует одновременно на огромное число малых масс термодинамической системы и они начинают вместе ускоренно двигаться. Появляется совместное движение, поток частиц. Всё предельно просто, исходя из имеющихся физических знаний о динамике малого (счётного) числа частиц. Сложность заключается в том что не всегда в неравновесной термодинамической системе (системе из не счётного числа частиц) под действием силы в соответствии с основным законом динамики происходит зримое ускорение массы, возникает кооперативное движение, совместный поток частиц. Для понимания причин этого необходимо уяснить очень важное для диссипативных сред понятие. Назовем его – диссипативный порог многочастичной системы. Всё дело в том, что как только в неравновесной многочастичной системе, в силу действия основного закона динамики, возник кооперативный поток, обладающий результирующим импульсом, то тут же начинает действовать механизм вырождения импульса, диссипирующий кооперативное движение.

Но прежде чем рассмотреть влияние на состояние и динамику диссипативной среды этих прямо противоположных, но всегда действующих в единстве процессов, рассмотрим закон сохранения и превращения энергии в применении к термодинамическим системам.

Существуют два вида энергии: -кинетическая энергия, энергия перемещения, энергия движения и - потенциальная энергия, энергия положения, зависящая от координат составляющих систему частиц. Кинетическую энергию и импульс всегда нужно рассматривать в единстве. Кинетическая энергия переносима импульсом. Импульс и кинетическая энергия две взаимосвязанные и дополняющие друг друга характеристики движения массы. Другое дело что кинетическая энергия в диссипативной среде существует в двух формах:

1) Кооперативная кинетическая энергия с (потоки энергии Умова-Пойтинга).

2)Тепловая форма кинетической энергии с

Но всегда 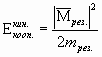и ;

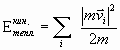- внутренняя энергия.

Причем тепловая форма кинетической энергии измеряется в системе центра масс.

Потенциальная энергия также связана с выделенным направлением по .

Закон сохранения и превращения энергии состоит из двух частей:

1). Сохранение энергии. Сумма кинетической и потенциальной энергии замкнутой сиcтемы остается постоянной не зависимо от протекающих в системе процессов.

(2)

2). Превращение энергии. При превращении одного вида энергии в другой выполняются равенства:

; ; ( 3 )

где: F - сила, - перемещение, - давление, - изменение объема.

Наряду с выделенным направлением для энергии важнейшим моментом, который необходимо отметить, является время. Изменения и превращения энергии не происходят вне динамики процессов, следовательно протекают во времени. Всё это в равной степени относится и к термодинамике, в том числе и классической, где процессы только обозначены в статике. Параметр времени в неявной форме присутствует во всех математических формулировках связанных с превращениями энергии, а в выражении (3), отвечающем за динамику процессов энергопревращений, он присутствует в явном виде. Превращение одного вида энергии в другой происходит при обязательном совершении работы, т.е. совершается перемещение под действием или против действующих сил. Силы в системе возникают только при наличии , т.е. если в системе есть неравновесность. Причем если перемещение возникает под действием сил, когда направление перемещения массы совпадает с направлением действующей силы, то происходит ускорение массы () и увеличивается кинетическая энергия, а значит соответственно уменьшается потенциальная энергия системы. Такие процессы наблюдаются при адиабатном расширении рабочего тела в сопле, при движении маятника вниз, при разрядке конденсатора и увеличении тока в колебательном контуре. Если перемещение происходит против действующих в системе сил, то увеличивается потенциальная энергия и работа совершается за счет уменьшения кинетической энергии и в системе накапливается неравновесность. Такие процессы наблюдаются при адиабатном сжатии в диффузоре, при перемещении маятника вверх, при зарядке конденсатора в колебательном контуре. И еще отметим: когда говорят о взаимопревращении тепловой, химической, механической и других видах энергии имеется в виду сохранение и взаимопревращение кинетической и потенциальной энергий в различных физических явлениях (тепловых, химических, механических и др.).

Подводя итог отметим, что в макро среде (сплошной среде), являющейся совокупностью огромного (не счётного) числа корпускул, может формироваться только четыре вида макроскопических потоков энергии в зависимости от свойств среды и природы разности потенциалов:

гидродинамический поток, когда разность потенциалов вызвана перепадом давлений или высот. Частный случай звуковой поток, когда происходит объёмное сжатие упругой среды.

фононный тепловой поток, когда разность потенциалов вызвана перепадом температур.

поток заряженных частиц (электрический ток), вызванный разностью электрических потенциалов.

Электромагнитный фотонный поток частиц (частный случай лазер), вызванный разностью потенциалов различных уровней энергии в атоме.

Именно эти четыре вида потоков энергии лежат в основе всех многочисленных, в том числе и очень сложных диссипативных структур.

Вернемся к рассмотрению событий в неравновесных диссипативных средах под влиянием совместного действия механизмов самоорганизации и релаксации, совместного действия в многочастичной среде 2-го закона Ньютона и эффекта вырождения результирующего импульса. Неравновесность состояния диссипативной среды, согласно идей выдвинутых Брюссельской школой, служит источником упорядоченности. Это необходимое, но не достаточное условие возникновения кооперативного движения, возникновения потоков энергии Умова-Пойтинга с . Необходимо также чтобы возникающий по причине неравновесности состояния системы поток тут же не рассеивался под действием причин релаксации. Выше уже отмечалось что как только в много частичной системе возник кооперативный поток, обладающий результирующим импульсом, то тут же начинает действовать механизм вырождения импульса, диссипирующий кооперативное движение. И теперь всё определяется мощностями этих двух прямо противоположных процессов, зависящих от состояния и свойств системы. Если мощность возникновения (производства) кооперативных потоков больше мощности процесса диссипации кооперативной энергии, то в системе наблюдаются кооперативные потоки, возникают потоки энергии Умова-Пойтинга, формируются диссипативные структуры. Если свойства системы по вырождению результирующего импульса таковы что превосходят по мощности возникающие кооперативные потоки, пропорциональные имеющейся в системе неравновесности, то в такой системе кооперативные потоки возникают в микро областях и тут же рассеиваются. В термодинамической системе в данной ситуации кооперативного движения не наблюдается, а идёт квазиравновесный процесс установления равновесия. Для возникновения кооперативного движения в диссипативной среде необходимо преодоление главного порогового соотношения. Мы назвали его диссипативным порогом.

где - энергия направленного кооперативного движения, переносимая результирующим импульсом и получаемая из потенциальной энергии неравновесности в единицу времени.

- максимальная энергия направленного кооперативного движения, переносимая результирующим импульсом, которую данная много частичная система способна в единицу времени переводить в хаотическую форму под действием причин релаксации.

Величина главного порогового соотношения, величина диссипативного порога определяется максимальной мощностью процесса релаксации, максимальной мощностью диссипации кооперативной кинетической энергии и является свойством, параметром данной много частичной системы.

Именно главное пороговое соотношение, определяющее соотношение между мощностью процесса самоорганизации и мощностью процесса диссипации определяет направление событий, направление эволюции в неравновесной диссипативной среде:

а) при - область линейной неравновесной термодинамики, когда мы говорим о локальном равновесии и не возникает потоков энергии с. В данной ситуации система под действием причин релаксации стремится к равновесию, к состоянию с и .

б) при - область нелинейной, сильно неравновесной термодинамики. При этом условии возникают потоки энергии Умова-Пойтинга с , происходит формирование диссипативных структур и появляется возможность совершать макроскопическую работу. Причём для получения кооперативного движения вовсе не обязательно чтобы в каждый момент времени мощность процесса производства кооперативного движения была больше мощности процесса вырождения результирующего импульса. Необходимо чтобы за наблюдаемый промежуток времени образовалось больше кооперативной энергии чем её диссипировало.

где: - мощность производства кооперативной энергии в неравновесной системе.

- это максимальная мощность кооперативной энергии, которую способна диссипировать данная термодинамическая система. Это важнейшая характеристика диссипативной системы.

Максимальная мощность диссипации кооперативной энергии – это характеристика присущая данной системе и зависящая от многих факторов (размеры системы, плотность частиц в системе, масса частиц, прочность связей между частицами, энергетическое состояние системы и её возможности по энергообмену с внешней средой и др.). Максимальная мощность процесса диссипации и есть тот порог не преодолев который не возможно в системе получить кооперативные потоки энергии, потоки Умова-Пойтинга, не возможно сформировать стабильную диссипативную структуру. Именно величина главного порогового соотношения, величина диссипативного порога присущая данной системе и определяет направление событий в данной системе.

Кстати наличие порогового соотношения качественно в термодинамике замечено уже достаточно давно. Так в (Л-7) автор пишет: "Таким образом, происходит своеобразное противоборство между процессами переноса, нарушающими равновесие, и внутренними (релаксационными) процессами, стремящимися его восстановить. В разреженном газе внутренние процессы - это процессы столкновения. Если процессы, возмущающие равновесие, менее интенсивны, чем процессы, которые его формируют, то можно говорить с определенной степенью точности о локальном равновесии в физически бесконечно малом объеме. Точность такого утверждения будет тем выше, чем меньше отношение скорости изменения состояния за счет внешних условий к скорости восстановления равновесия за счет внутренних релаксационных процессов. Подчеркнем, что существование локального равновесия еще не означает малости отклонения всей системы от равновесия". От себя добавим, что для возникновения потоков энергии Умова-Пойтинга, для формирования диссипативных структур вовсе не обязательно наличие общей сильной неравновесности системы. И процессы самоорганизации и процессы диссипации энергии зависят от многих причин, от них зависит и величина диссипативного порога главного порогового соотношения.

Рассмотрим поведение диссипативной системы при ее нахождении по ту или иную сторону от диссипативного порога.

а) при потоки энергии образуются в микрообластях и тут же рассеиваются. Вся потенциальная энергия неравновесности сразу переходит в хаотическую форму и не способна производить макроскопическую работу. В зоне локального равновесия также существуют потоки энергии от высшего потенциала к низшему, но из-за того что эти потоки не обладают кооперативным движением, т.е. у них , то эти потоки не способны совершать макроскопическую работу, а стало быть и резкие видоизменения (бифуркации) в среде. Эти потоки приводят только к постепенному изменению системы к состоянию равновесия. Отнесём к потокам энергии Умова-Пойтинга только потоки энергии, имеющие , т.е. обладающие кооперативным движением. Возникновение этих потоков и есть результат самоорганизации кооперативного движения в диссипативной среде. Из выше сказанного и понимания механизма релаксации легко видна справедливость универсального критерия эволюции Гленсдорфа-Пригожина. Согласно этому критерию, в любой неравновесной системе с фиксированными граничными условиями процессы идут так, что скорость изменения производства энтропии, обусловленная изменением термодинамических сил, уменьшается. Из механизма релаксации вытекает что в неравновесной системе, где безгранично действуют причины релаксации и из вне не поддерживается неравновесность неизбежно наступает равновесие, а из рисунка -1, поясняющего механизм релаксации, видно что после первого соударения частицы ее направленная энергия уменьшилась в двое. Затем уже после столкновения двух движущихся частиц оставшаяся направленная энергия снова уменьшилась вдвое, но это уже будет четвертая часть от первоначально направленной энергии и так далее. По мере развития процесса релаксации доля направленной энергии переходящая в хаотическую уменьшается, а следовательно уменьшается производство энтропии и ее производная отрицательна. Условие а) -определяет направление эволюции неравновесной системы к равновесию.

б) При выполнении данного условия в неравновесной системе возникают потоки направленной кинетической энергии, связанной с результирующим импульсом, и у системы появляется возможность совершать макроскопическую работу, при этом в системе формируется динамический процесс. Происходит первая бифуркация, в диссипативной среде формируется диссипативная структура. Диссипативная структура в зависимости от конкретных условий имеет определенные пространственные и временные рамки. Для открытой диссипативной структуры возможны три варианта развития:

Вариант 1): при равенстве подводимого из вне потока энергии для поддержания неравновесности и отводимой во внешнюю среду диссипированной энергии и энтропии, полученной в результате диссипации кооперативного движения при функционировании структуры плюс внешняя работа, структура может существовать сколь угодно долго.

(4)

Назовем ( 4 ) соотношением стабильности. Для отдельного процесса это условие его стационарности, для сложной диссипативной структуры, состоящей из согласованно действующей совокупности многих процессов, это условие её существования во времени.

Мы не говорим о внесении отрицательной энтропии. Мы говорим о подводе в открытую систему потенциальной или направленной энергии для подержания неравновесности, энтропия которой равна нулю. А отводим в окружающую среду диссипированную энергию, в результате энтропия закрытой системы (диссипативная структура + окружающая среда) возрастает.

По причине того, что в стационарных процессах действие причин релаксации ограничено (энергия передается на ограниченную массу, когерентность делает соударение близким к центральному удару, что также снижает рассеяние) по сравнению с условиями когда в процессе релаксации масса вовлекается лавинообразно, то становятся понятными принцип Онсагера о минимальном рассеянии энергии и принцип Пригожина о минимальном производстве энтропии в стационарных процессах.

Вариант 2):

Здесь также возможны два случая: во-первых весь избыток направленной энергии, получаемый диссипативной структурой сверх необходимого для функционирования самой структуры, структура расходует на совершение внешней работы и может как и в варианте 1) существовать сколь угодно долго. Во-вторых, если внешняя работа не совершается, идет накопление кооперативной энергии или неравновесности в системе и диссипативная структура идет к новой бифуркации, в результате которой формируется новое состояние, новая диссипативная структура. Принципиальный механизм бифуркации одной диссипативной структуры в другую заключается в следующем: при нарастании кооперативной энергии или неравновесности в диссипативной структуре, за счет увеличения мощности преобразования потенциальной энергии в направленную кинетическую, возникает излишнее для данной диссипативной структуры направленное кооперативное движение, способное совершать работу по преодолению оказывающихся на его пути потенциальных барьеров. Момент времени и совершаемая при этом работа и представляют собой бифуркацию: переход одной диссипативной структуры в другую. Бифуркации возникают не спонтанно, а в момент преодоления потенциального барьера, возникающего на пути кооперативного движения. Если после бифуркации в новой диссипативной структуре устанавливается равновесие по варианту 1), то новая структура будет устойчивой. Если в новой диссипативной структуре вновь при определенных условиях с некоторого момента начинает накапливаться кооперативная энергия или неравновесность, то система вновь готова к очередной бифуркации, к формированию последующей структуры. Описанное выше представляет собой механизм, динамику эволюции структур. Потенциальные барьеры, встающие на пути кооперативного движения, могут иметь самую различную величину и форму и тем самым определяют величину кооперативной энергии которую должна приобрести диссипативная структура для последующей бифуркации. Потенциальные барьеры, несмотря на самую различную величину и форму, по своей природе бывают только двух типов: создаваемые силами притяжения или силами отталкивания. На величину кооперативной энергии, необходимую для бифуркации данной структуры может влиять присутствие катализаторов, способствующих преодолению барьеров. Величина производства энтропии от одной диссипативной структуры к другой не имеет никакой тенденции, а определяется механизмом релаксации данной структуры, мощностью диссипации направленной энергии и отводом ее в окружающую среду. За главным пороговым соотношением, в зоне эволюции структур, энтропия не играет ту фундаментальную роль как в зоне локального равновесия. При эволюции структур вновь на первое место выходят законы динамики в понимании динамики Ньютона, главенствует эволюционный детерминизм. Хотя фундаментальное свойство диссипативных систем, их способность вырождать результирующий импульс, постоянно присутствует в жизни диссипативной структуры, определяя характер и время ее существования. Рассмотрим это в третьем варианте существования диссипативной структуры.

Вариант 3):

Как только выполняется условие 3), то диссипативная структура начинает затухать и разрушаться. Диссипативная система переходит на низшую структуру, а если затухающая диссипативная структура сложная, например биоструктура, состоящая в свою очередь из совокупности согласованных подпроцессов, подсистем, то такая структура или разрушается совсем, вплоть до равновесного состояния или должна восстановить равновесие соответствующее данной диссипативной структуре.

Принципиальная схема эволюции неравновесных диссипативных систем изображена на Рис. – 3.

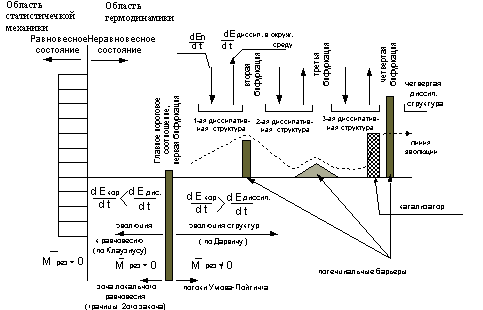
Рис. 3

Необходимо также отметить, что оба противоположных направления эволюции диссипативных систем протекают благодаря имеющейся в природе неравновесности и срабатывают ее, диссипируя кооперативное движение. Таким образом, если в природе не будет процессов по воссозданию неравновесности из уже равновесной подсистемы общей энергии Вселенной, то, исходя из закона сохранения энергии, Клаузиус прав в своем выводе о тепловой смерти Вселенной.

Подчеркнём, что динамика много частичных сред отличается от хорошо изученной динамики малого числа взаимодействующих частиц тем, что в много частичной среде на известные законы динамики накладывается эффект вырождения результирующего импульса. Следствием эффекта вырождения импульса становится присущий каждой многочастичной системе диссипативный порог, разделяющий динамику многочастичной среды на два направления эволюции: по Клаузиусу – в направлении равновесного состояния, соответствующего максимуму энтропии и по Дарвину – в направлении формирования и усложнения диссипативных структур.

Хотелось бы особо отметить, что эффект вырождения результирующего импульса ни в коей мере не противоречит ни работам Больцмана и всему, что с ними связано, ни работам Пригожина и всему, что с ними связано. Напротив, эффект вырождения результирующего импульса является тем мостом, который связывает воедино всю классическую динамику от динамики Ньютона до динамики структур Пригожина и является фундаментом для идей Больцмана. Именно эффект вырождения результирующего импульса приводит к единообразию описания природы, т.к. вся классическая динамика от динамики Ньютона (динамики счётного числа частиц) до динамики не счётного числа частиц (термодинамика, теплопередача, гидродинамика, электродинамика токов, биофизика) строится исходя из трёх постулатов, лежащих в основе динамики Ньютона:

1) закон сохранения и превращения энергии;

2) закон сохранения результирующего импульса (момента импульса);

3) корпускулярный характер строения материи.

Эффект вырождения результирующего импульса объёдиняет также оба направления эволюции (по Клаузиусу и по Дарвину), объясняя их с единых позиций.

В [Л-6] И. Пригожин пишет: “… мы вправе задать фундаментальные вопросы: какое место занимают необратимые процессы в нашем описании физического мира? Как эти процессы связаны с динамикой?”. Надеюсь нам здесь удалось дать ответы на эти вопросы.

Диссипативная структура и её характеристики

Диссипативная структура – важнейшее и относящееся к числу наиболее общих и сложных из понятий макромира. Достаточно сказать, что под это понятие подпадают турбулентность и ячейки Бенара, электрические токи и лазеры, все виды биологических и технических (например, автомобиль и компьютер) структур, производственные структуры. Без этого понятия невозможно объяснить и описать изменчивость и эволюцию окружающего макромира.

Мы уже выяснили, что диссипативная структура возникает в неравновесной многочастичной системе тогда, когда в этой системе или какой-то её локальной зоне формируются условия, при которых производство кооперативной энергии превосходит её диссипацию вызванную нецентральным соударением. Это достигается или увеличением неравновесности или снижением диссипативного порога, или и тем и другим одновременно. Увеличение неравновесности достигается увеличением какой-либо разности потенциалов, увеличением градиента потенциальной энергии, что приводит к увеличениею сил, действующих в неравновесной системе. Снижение диссипативного порога системы или какой-то её локальной зоны достигается созданием условий при которых ограничивается лавинообразное вовлечение массы (количества частиц) в результирующий импульс кооперативного движения. Это достигается или канализацией потока или централизацией соударения частиц, созданием условий для когерентного взаимодействия частиц. Вообще применительно к диссипативной структуре необходимо учитывать три мощности: это мощность кооперативных потоков энергии Умова- Пойтинга, она определяется количеством кинетической энергии проходящей через сечение потока в единицу времени, мощность производства кооперативных потоков энергии Умова-Пойтинга, этот процесс вызван основным законом динамики и мощность диссипации кооперативных потоков энергии Умова-Пойтинга, этот процесс вызван эффектом вырождения результирующего импульса в многочастичной среде.

Мощность процесса самоорганизации энергии зависит от величины неравновесности (определяющей величину силы действующей в системе, ) и условий в которых протекает процесс. Если при заданной температурной неравновесности тепло передается через тонкий стержень с плохой теплопроводностью, то это одна мощность теплового потока, если при той же температурной неравновесности тепло передается через большую, тонкую поверхность с хорошей теплопроводностью, то мощность теплового потока в последнем случае может быть на много порядков больше. Аналогичная ситуация возникает и при любой другой неравновесности. Скажем неравновесность по давлению можно срабатывать через одно сопло с малым проходным сечением, а можно через сколь угодное количество таких же сопел одновременно. Неравновесность по электрическому напряжению можно с малой мощностью срабатывать через большое электрическое сопротивление, а можно через короткое замыкание вызвать большие мощности.

Таким образом у нас имеется возможность управлять процессами самоорганизации и диссипации энергии и преодолевать в ту или другую сторону диссипативный порог, то есть создавать структуру или разрушать её. В связи с этим исключительно важным для существования диссипативной структуры во времени является соблюдение соотношения стабильности. Сложная диссипативная структура, например биоклетка, может состоять из совокупности подсистем или подпроцессов. Но тем не менее для каждой подсистемы сложной системы должны выполняться, с определенными допустимыми вариациями, соотношения стабильности (4). Процессы могут носить равномерный или циклический характер, приводящий то к накоплению неравновесности, то к ее срабатыванию. То к накоплению диссипированной энергии и энтропии, то к их сбросу в окружающую среду. Однако с поправкой на время соотношение стабильности должно для стабильно функционирующей структуры выполняться безукоризненно, в том числе и на период видоизменения (например деления клетки) диссипативной структуры. И сам разброс от соотношения стабильности имеет для каждой структуры свои границы, за пределами которых или новая бифуркация (вариант 2) или разрушение (вариант3). Следует отметить, что соотношение стабильности определяет соотношение энергетических потоков. Но если в связанных системах (кристалл) реализуются только потоки энергии, то в системе не связанных частиц энергопотоки сопровождаются и массовыми потоками, обеспечивающими скажем клетку строительным материалом для роста и размножения.

Соотношения стабильности (4) представляют собой согласованные в своем развитии во времени функции процессов составляющих структуру и зависящие не только от времени, но и многих управляющих параметров, от которых в свою очередь зависят мощности процессов преобразования неравновесности в корпоративное движение, диссипации кооперативного движения и отвода диссипированной энергии в окружающую среду. Таким образом соотношение стабильности отвечает на энергетическом уровне за согласованность всей совокупности процессов, обеспечивающих функционирование диссипативной структуры.

Изменение по каким-либо причинам управляющих параметров приводят к рассогласованности соотношений стабильности и диссипативная структура начинает развиваться по варианту 2) или 3) или обязана восстановить соотношения стабильности. При этом управляющие параметры могут влиять как на величину неравновесности системы, то есть на производство кооперативной энергии, так и на величину диссипативного порога, то есть на процесс диссипации кооперативной энергии.

Диссипативная структура представляет собой двуединую сущность, совокупность статической и динамической структур. Статическая структура обеспечивает выход неравновесной системы или её локальной части за диссипативный порог за счёт обеспечения канализации потока или за счёт обеспечения когерентного взаимодействия. А за диссипативным порогом формируются динамические структуры, потоки энергии, имеющие результирующий импульс отличный от нуля. Динамическая подструктура обеспечивает функциональные возможности дисипативной структуры, то есть работу против внешних сил и против внутренних сил трения, вызванных нецентральным соударением. Причём всё многообразие диссипативных структур образовано как уже отмечалось ранее четырьмя видами динамических структур, четырьмя видами потоков энергии.

Всякая диссипативная структура – это двигатель по преобразованию потенциальной энергии неравновесности (в том числе и тепловой) многочастичной системы в кооперативную энергию потоков (в механическую энергию, в работу на языке классической термодинамики). Всякой диссипативной структуре для существования, для выполнения функциональных возможностей необходима механическая энергия и она получается в самой структуре. Собственно производство кооперативной энергии и есть сама сущность диссипативной структуры. Если в системе создаются условия для преобразования неравновесности в кооперативные потоки, то есть система выходит за диссипативный порог, то начинается процесс преобразования тепла (потенциальной энергии неравновесности термодинамической системы) в работу (в кооперативную энергию потоков, в механическую энергию). Механизм преобразования тепла в работу лежит в основе формирования и существования диссипативных структур. Понятие диссипативная структура и процесс преобразования тепла (неравновесности) в работу связаны теснейшим образом. Рассмотрим это на нескольких примерах:

а) тепловые машины. Всякий двигатель, в том числе и тепловой, превращает потенциальную энергию неравновесности в кооперативную энергию потоков энергии. Причём это обязательно происходит за диссипативным порогом и в рамках соотношения стабильности (4). Если скажем в нарушение соотношения (4) на электростанции закончится топливо, то прекратится производство кооперативной энергии, в том числе по цепочке и электрической и остановятся электродвигатели потребителей. Структура разрушится. Этот простейший пример показывает единство принципов функционирования диссипативных структур и любых, в том числе и тепловых двигателей.

б) гидродинамические потоки. Такие диссипативные структуры как ламинарный и турбулентный потоки и ячейки Бенара являются ни чем иным как двигателями преобразующими в одном случае неравновесность по давлению в другом неравновесность по температуре в кооперативную (механическую) энергию гидропотоков. Причём если для случая допустим ячеек Бенара, при неизменном перепаде температур по сторонам слоя, увеличивать толщину слоя, то ситуация перейдёт в зону локального равновесия, производство потоков энергии Умова прекратится и структура разрушится. Подробнее о физике турбулентности и ячеек Бенара можно прочесть на сайте SciTecLibrary.com в разделе “статьи и публикации”.

в) биоклетка. Последовательность сменяющих друг друга экзотермических реакций окисления и эндотермических реакций синтеза создаёт в клетке неравновесность по температуре и давлению. Это приводит к возникновению гидродинамических потоков биологического раствора, что и обеспечивает метаболизм в клетке. Причём снижение диссипации кооперативной энергии в клетке и вывод ситуации за диссипативный порог обеспечивается канализацией потока в эндоплазматической сети. В каждой клетке действует биологический двигатель внутреннего сгорания, обеспечивающий функциональные возможности клетки. Скажем, окислительные реакции, протекающие в митохондриях клетки или реакции цикла Кребса, в которых высвобождается и запасается большая часть энергии, по праву получили название – энергетический котёл. В митохондриях локализованы и ферменты, катализирующие окислительные реакции. Энергетический котёл митохондрий соответствует котельным установкам или камерам сгорания технических устройств. Подробнее о биодинамике клетки можно прочесть на сайте SciTecLibrary.com в разделе “статьи и публикации”.

В связи с описанными примерами логично встаёт вопрос о компенсации за преобразование тепла в работу, понятии являющемся одним из краеугольных камней термодинамики. Неравновесность (потенциальная составляющая внутренней энергии тепловой системы) преобразуется в кооперативную энергию (механическую работу) благодаря действию основного закона динамики, а компенсация за преобразование тепла в работу вытекает из этого процесса как следствие и вызвана процессами диссипации, действием эффекта вырождения результирующего импульса.

Компенсация за преобразование тепла в работу вытекает из неравновесности многочастичной системы. Неравновесность приводит в действие основной закон динамики, который преобразовывает потенциальную энергию системы в кооперативную энергию потока, совершая при этом работу по преобразованию потенциальной энергии в кинетическую (в механическую работу, в техническую работу по терминологии классической термодинамики). Корпускулярный характер системы, в которой развиваются выше описанные события вызывает к действию эффект вырождения возникшего результирующего импульса, приводящий к частичной или полной диссипации произведённой кооперативной энергии. Диссипация возникающей кооперативной энергии и есть компенсация за преобразование тепла в работу. Она может быть полной, если процессы протекают в зоне локального равновесия, может быть частичной, если процессы протекают за диссипативным порогом. А может и стремиться к нулю, если стремить к нулю диссипативный порог неравновесной системы, в которой происходит преобразование потенциальной энергии неравновесности в кооперативную энергию потоков. Эта компенсация свойственна всем без исключения диссипативным структурам, так как свойство производства кооперативных потоков – главное свойство диссипативных структур. Это в равной степени относится и к сегодняшним техническим устройствам, к тепловым двигателям. Но для сегодняшних тепловых двигателей это только часть компенсации за преобразование тепла в работу, причём меньшая её часть.

Не нужно путать компенсацию за преобразование потенциальной энергии неравновесности в кооперативную энергию, вызванную нецентральным соударением, с компенсацией в тепловых машинах работающих с термическим КПД всегда меньшим единицы. Это совершенно разные понятия и явления. Даже когда в классической равновесной термодинамике мы рассматриваем идеальные обратимые процессы, идущие без трения, то и здесь имеем термический КПД меньший единицы, достигающий максимума в идеальных циклах Карно. Термический КПД не имеет никакого отношения к диссипации, к универсальным механизмам преобразования неравновесности термодинамических систем в кооперативную энергию. Термический КПД вызван необходимостью затраты механической энергии на работу по проталкиванию рабочего тела в атмосферу, на работу по расширению атмосферы, на работу против сил гравитации.

Компенсация за преобразование тепла в работу в современных тепловых машинах складывается из двух составляющих:

1) Первая составляющая, вызванная эффектом вырождения импульса или по попросту трением. Её доля в современных тепловых машинах определяется как произведение трёх КПД: внутреннего относительного КПД проточной части, электромеханического КПД и КПД потерь теплового потока через поверхности. Эта совокупная доля – малая величина, которую можно стремить к нулю, снижая диссипативный порог системы. Примером резкого снижения компенсации данного вида может служить конструкция термоэлектрического преобразователя на основе нанотехнологий. Внутреннее электрическое сопротивление данного преобразователя, а стало быть и диссипативный порог снижены в миллионы раз в сравнении с ныне действующими. Подробно о термоэлектрическом преобразователе принципиально новой конструкции можно подробно прочесть на сайте SciTecLibrary.com в разделе “статьи и публикации”.

2) Вторая составляющая вызвана необходимостью производства работы по расширению атмосферы, работы против сил гравитации. Её доля определяется термическим КПД цикла, эталоном которого является КПД Карно. Это львиная доля потерь современных тепловых машин. В классической термодинамике под компенсацией за преобразование тепла в работу понимается именно вторая составляющая. К понятию компенсации в классической термодинамике пришли на основании анализа идеальных обратимых циклов, в первую очередь цикла Карно, в которых диссипация (трение) отсутствуют по определению. Подробно эта тема развита на на сайте SciTecLibrary.com в разделе “статьи и публикации”. В статье не только показана природа и причины этих потерь, но и показаны способы их резкого сокращения.

Коридор эволюции, становление и конечная предопределённость эволюции

Как следует из ранее изложенного эволюционное развитие неравновесных макросистем обеспечивает противоборство между основным законом динамики и эффектом вырождения результирующего импульса в многочастичной среде.

Согласно закона сохранения и превращения энергии всякое изменение (эволюция) в природе происходит под действием сил, совершающих работу. Если нет сил или они не совершают работу, то нет преобразования видов энергии, нет изменений, нет эволюции диссипативных систем. Учитывая что в реальности существует огромное количество разнообразных по величине и природе потенциалов (более 100 химических элементов, несколько миллионов химических соединений на их основе, многообразие физических и иных явлений и образований), то при соприкосновении в силу тех или иных причин этих разных по уровню потенциалов возникают неравновесности, градиенты потенциалов и силы. Появляется возможность в диссипативных системах к совершению работы, изменениям, эволюции. При отмеченном многообразии и изначальной неравновесности природы эволюция диссипативных систем предопределена. Вот почему мы говорим об эволюционном детерминизме, базирующимся на фундаментальных законах динамики в применении к диссипативным средам. Даже порождение хаоса - флуктуации в диссипативной системе или структуре могут способствовать увеличению неравновесности и стало быть преодолению потенциальных барьеров, т.е. способствовать образованию структуры или эволюции к другой диссипативной структуре. Мы здесь имеем в виду структуры вне области релятивистской и микро физики, а также макрокосмоса.

Когда под действием внешних или внутренних причин изменение управляющих параметров приводит к формированию новой диссипативной структуры, может появиться, особенно для сложной структуры, несколько разновидностей структуры (различные мутации в биологии) с различной степенью приближения к соотношениям стабильности для данной диссипативной структуры. Выживают те разновидности структуры, которые наиболее активны и устойчивы в рамках соотношения стабильности. В этом заключается закон естественного отбора Дарвина.

В рамках многообразия возможных неравновесностей отмеченных выше, возможно формирования и многообразия диссипативных структур. Это конечное многообразие. В области этого конечного многообразия и протекают различные линии эволюции от структуры к структуре, которые могут оказывать друг на друга влияние. Многообразие всевозможных диссипативных структур макромира конечно, если под различными структурами не понимать, например ламинарный поток в трубах различного диаметра. Ведь диаметров может быть бесконечное множество. Ламинарные потоки, возникающие в трубах различного диаметра за счёт перепада давления качественно не отличаются друг от друга. Под разными диссипативными структурами будем понимать структуры отличающиеся друг от друга по качественным признакам, например ламинарный и турбулентный потоки. Или ламинарный поток в канале за счёт перепада давления и ламинарный поток в ячейках Бенара за счёт перепада температур. При всём многообразии возможностей для прохождения линии эволюции, она протекает в рамках своего коридора эволюции. Коридор эволюции определяется величиной потенциальных барьеров статической подструктуры диссипативной структуры. Скажем в гидродинамическом потоке в качестве таких барьеров выступает прочность канала (трубы) и силы связи между частицами жидкости. Если прочность трубы не достаточна, она разрушается, что приведёт к разрушению диссипативной структуры гидродинамического потока. Величина связи частиц в жидкости влияет на момент начала бифуркации и перехода ламинарного течения в турбулентное. В биологии рамки определяются в числе прочего перепадами температур в которых возможно протекание биологических процессов. В биологии широк спектр возможных структур и вариантов развития, а значит и возможностей для отбора. Любая линия эволюции, протекающая в границах своего коридора, благодаря отбору стремится к наиболее устойчивой в данных условиях структуре. Этим и определяется конечная предопределённость эволюции в условиях конкретной действительности.

Зная природные условия на Земле, их изменения во времени, можно в принципиальных основах реконструировать все этапы становления эволюции, в том числе и биологической эволюции, из всего многообразия возможностей.

Заключение

Время – это просто скорость равномерного периодического процесса принятая в качестве эталона сравнения. Направление числовой оси времени связано с линией эволюции, причинно-следственная последовательность которой предопределена необратимостью процессов протекающих в диссипативных средах. Необратимость процессов вызвана необратимостью эффекта вырождения результирующего импульса. Сам же эффект вырождения результирующего импульса порождён корпускулярным характером строения материи. Корпускулярный характер материи приводит к формированию многочастичных систем, состоящих из не счётного числа частиц конечных размеров. Конечный размер корпускул становится причиной нецентрального соударения, что в совокупности с несчётным числом корпускул приводит к необратимому рассеянию кооперативной энергии.

Совместное действие в многочастичной среде основного закона динамики и эффекта вырождения результирующего импульса в условиях за диссипативным порогом системы приводит к формированию диссипативных структур. Главной сутью диссипативной структуры является производство кооперативной энергии (механической работы) из потенциальной энергии неравновесности. Произведённая кооперативная энергия позволяет совершать работу необходимую для эволюционного развития от простейших структур не живой природы до высоко организованных биоструктур сегодняшнего дня.

В заключение отметим основные этапы становления сегодняшнего дня:

- ПЕРВЫЙ ЭТАП: “В начале сотворил Бог небо и землю. Земля же была безвидна и пуста, и тьма над бездною; и Дух Божий носился над водою”. Библия, первая книга Моисеева.

Здесь заложены законы детерминизма – закон сохранения и превращения энергии и закон сохранения результирующего импульса (момента импульса).

- ЭТАП ВТОРОЙ: “И сказал Бог: да будет свет. И стал свет”. Библия, первая книга Моисеева.

Совершена работа по созданию неравновесности, которая в процессе эволюционного развития на уровне микромира привела от события большого взрыва к таблице Менделеева, к корпускулярному характеру строения материи.

На этом этапе заработал эффект вырождения результирующего импульса.

- ТРЕТИЙ ЭТАП СТАНОВЛЕНИЯ: Этап макроэволюции. От таблицы Менделеева по коридору эволюции к сегодняшнему дню, к обществу человека разумного, как мы сами себя называем.

Но это ещё не полное становление. ЦЕЛЬ – быть подобными Тому по образу Которого мы сотворены и тогда радость, порождаемая Духом Божиим, поселится в душах наших. Тьма невежества рассеется и станет светло на душе.

Список литературы

Базаров И.П. Термодинамика. – г. Москва, из-во “Высшая школа”, 1991г.

Гельфер Я.М. История и методология термодинамики и статистической физики. – г. Москва, из-во “Высшая школа”, 1981г.

Косарев А.В. Динамика эволюции неравновесных диссипативных сред. – г. Оренбург, ИПК ”Оренбурггазпромпечать”, 2001г.

Николис Г., Пригожин И. Самоорганизация в неравновесных системах. – г. Москва, из-во “Мир”, 1979г.

Пригожин И., Стенгерс И. Время, хаос, квант. – г. Москва, из-во “Прогресс”, 1994г.

Пригожин И. От существующего к возникающему. – г. Москва, из-во “Наука”, 1985г.

Осипов А.И. Самоорганизация и хаос. – г. Москва, из-во “Знание”, 1986г.

Для подготовки данной работы были использованы материалы с сайта http://www.sciteclibrary.ru