
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология и педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по информатике программированию
Краткое содержание произведений
Реферат: Модель теплового состояния аппарата сепарации
Реферат: Модель теплового состояния аппарата сепарации
Ставится задача определения времени, необходимого для окончания процесса сепарации аппарата восстановления титана, и теплового состояния сепарируемой массы во время процесса.
Нагрев аппарата происходит в три стадии:
Прогрев реакционной массы. Оканчивается, когда на внутренней поверхности стенки аппарата достигается температура кипения магния, соответствующая поддерживаемому в аппарате давлению.
Кипение летучих. Будем полагать, что фронты кипения Mg и MgCl2 движутся поступательно внутрь аппарата от стенки, образуя коаксиальные цилиндрические поверхности (см. рис. ниже).
Стадия конечного прогрева после выкипания большей части летучих. Тепловые свойства аппарата определяются свойствами титановой губки.
Аппарат
находится в
печи сепарации.
Тепло к нему
подводится
вследствие
теплообмена
излучением
с нагревателями
печи и конвективного
теплообмена
с воздухом,
заполняющим
печь. В первом
приближении,
суммарный
тепловой поток
![]() ,
воспринимаемый
аппаратом,
можно выразить
как
,
воспринимаемый
аппаратом,
можно выразить
как
![]() ,
,
где
![]() –
температура
наружной поверхности
стенки аппарата,
–
температура
наружной поверхности
стенки аппарата,
![]() – температура
нагревателей,
– температура
нагревателей,
![]() – температура
воздуха в печи,
– температура
воздуха в печи,
![]() – коэффициент
теплоотдачи
при свободной
конвекции,
– коэффициент
теплоотдачи
при свободной
конвекции,
![]() – интегральный
коэффициент
теплопередачи
излучением,
зависящий от
степени черноты
тел и углового
коэффициента
облучения.
– интегральный
коэффициент
теплопередачи
излучением,
зависящий от
степени черноты
тел и углового
коэффициента
облучения.
Для системы печь – аппарат можно принять коэффициент теплопередачи излучением
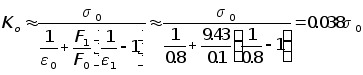 ,
,
где
![]() Вт/(м2К4),
Вт/(м2К4),
![]() ,
,
![]() м2 – площадь
излучателей
(нагревателей
печи),
м2 – площадь
излучателей
(нагревателей
печи),
![]() м2 – площадь
поверхности
аппарата,
м2 – площадь
поверхности
аппарата,
![]() м
– радиус аппарата,
м
– радиус аппарата,
![]() м – высота аппарата.
м – высота аппарата.
Коэффициент лучистого теплообмена для системы воздух – аппарат определяется, исходя из парциальных давлений паров воды и углекислого газа. В рассматриваемых условиях наличие паров воды маловероятно, а коэффициент теплового излучения CO2 в интервале температур 600...1200 оС близок к 0.3, то есть
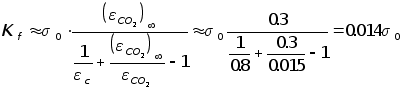 ,
,
где
![]() –
коэффициент
излучения
углекислого
газа заданной
толщины (0,25 м) и
парциального
давления (0.005 атм),
–
коэффициент
излучения
углекислого
газа заданной
толщины (0,25 м) и
парциального
давления (0.005 атм),
![]() – то же для условно
бесконечного
слоя.
– то же для условно
бесконечного
слоя.
Аналогичным образом можно записать тепловые потоки для нагревателей печи и воздуха, заполняющего печь.
Расход тепла из аппарата происходит излучением через крышку в реторту-конденсатор:
![]()
где
![]() – коэффициент
теплопередачи
от аппарата
к реторте-конденсатору,
– коэффициент
теплопередачи
от аппарата
к реторте-конденсатору,
![]() – температура
реторты-конденсатора
( 390 К).
– температура
реторты-конденсатора
( 390 К).
Согласно
записанным
выше соображениям,
порядок
![]() можно оценить
следующим
образом:
можно оценить
следующим
образом:
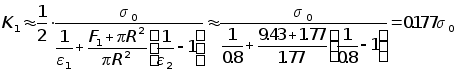 .
.
Множитель 1/2 принят из-за того, что между аппаратом и конденсатором находится тепловой экран, как минимум вдвое снижающий лучистый тепловой поток.
Кроме того, происходит унос тепла вместе с продуктами возгонки. Оценить его можно, только достоверно зная массовый поток и температуру сублимированных продуктов. Этот вопрос выходит за рамки настоящего исследования.
На первой стадии можно рассматривать аппарат как сплошное цилиндрическое тело. Задача нагрева бесконечного цилиндра, помещенного в подогревающую среду, имеет аналитическое решение
![]() ,
,
где
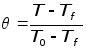 – относительная
температура,
– относительная
температура,
![]() – температура
цилиндра на
радиусе
– температура
цилиндра на
радиусе
![]() ,
,
![]() – начальная
температура
цилиндра (до
нагрева),
– начальная
температура
цилиндра (до
нагрева),
![]() – температура
подогревающей
среды (воздуха
в печи),
– температура
подогревающей
среды (воздуха
в печи),
![]() – n-й корень
характеристического
уравнения
– n-й корень
характеристического
уравнения
![]() ,
,
![]() – критерий Био,
– критерий Био,
![]() – коэффициент
теплоотдачи
от подогревающей
среды,
– коэффициент
теплоотдачи
от подогревающей
среды,
![]() – радиус аппарата,
– радиус аппарата,
![]() м,
м,
![]() – коэффициент
теплопроводоности
материала
цилиндра,
– коэффициент
теплопроводоности
материала
цилиндра,
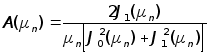 ,
,
![]() – коэффициенты,
– коэффициенты,
![]() – критерий
Фурье,
– критерий
Фурье,
![]() – коэффициент
температуропроводности
материала
цилиндра,
– коэффициент
температуропроводности
материала
цилиндра,
![]() – плотность
материала
цилиндра,
– плотность
материала
цилиндра,
![]() – теплоемкость
материала
цилиндра,
– теплоемкость
материала
цилиндра,
![]() – время прогрева,
– время прогрева,
![]() – функция Бесселя
k-го порядка,
являющаяся
решением уравнения
– функция Бесселя
k-го порядка,
являющаяся
решением уравнения
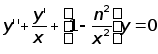 ;
;
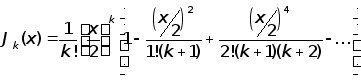 .
.
Оценим порядок критериев, входящих в это уравнение.
По окончании процесса восстановления в аппарате содержится порядка 60% (массовых) Ti, 20...30% Mg и 10...20% MgCl2. Плотность титана 4.35, магния 1.8, MgCl2 порядка 2.7, следовательно, средняя плотность реакционной массы
![]() кг/м3.
кг/м3.
Примем следующие зависимости от температуры теплофизических параметров:
![]() Дж/(кг К) в твердом
состоянии,
Дж/(кг К) в твердом
состоянии,
![]() Дж/(кг К) в жидком
состоянии,
Дж/(кг К) в жидком
состоянии,
![]() Дж/(кг К) в твердом
состоянии
Дж/(кг К) в твердом
состоянии
![]() Дж/(кг К) в жидком
состоянии,
Дж/(кг К) в жидком
состоянии,
![]() Дж/(кг К),
Дж/(кг К),
![]() Вт/(м К) в твердом
состоянии
Вт/(м К) в твердом
состоянии
![]() Вт/(м К) в жидком
состоянии
Вт/(м К) в жидком
состоянии
![]() Вт/(м К)
Вт/(м К)
![]() Вт/(м К)
Вт/(м К)
![]() кДж/кг
кДж/кг
![]() кДж/кг
кДж/кг
Таким образом, при температуре 800 К, средней в рассматриваемом диапазоне, средняя теплоемкость аппарата
![]() Дж/м3.
Дж/м3.
и средняя теплота парообразования
![]() кДж/моль.
кДж/моль.
Теплопроводность титановой губки можно оценить по соотношению
![]() ,
,
где
![]() – теплопроводность
титана,
– теплопроводность
титана,
![]() Вт/(м2К),
Вт/(м2К),
![]() –
пористость
титановой губки
(отношение
объема пор к
общему объему).
–
пористость
титановой губки
(отношение
объема пор к
общему объему).
| Пористость губки |
Теплопроводность, Вт/(м2К), |
| 0.2 | 14.0 |
| 0.3 | 11.0 |
| 0.4 | 8.0 |
При
средней пористости
блока 0.2...0.3 можно
принять
![]() .
.
Порядок средней теплопроводности аппарата в целом можно оценить, исходя из массового состава блока:
![]() Вт/(м2К).
Вт/(м2К).
Тогда
коэффициент
температуропроводности
изменяется
в пределах
![]() ,
а число Фурье
,
а число Фурье
![]() .
.
Так
как время прогрева
порядка нескольких
часов или даже
суток, то величина
![]() .
При больших
значениях
.
При больших
значениях
![]() достаточно
одного члена
ряда:
достаточно
одного члена
ряда:
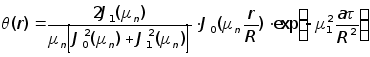 .
.
Оценим
порядок критерия
Био. Коэффициент
теплопередачи
при свободной
конвекции (cм.
ниже) можно
принять порядка
8...10. Тогда для
аппарата диаметром
1.5 метра среднее
значение
![]() .
При малых
.
При малых
![]() можно считать,
что температура
прогреваемого
цилиндра по
всему сечению
близка к одинаковой,
то есть равна
температуре
на поверхности
аппарата.
можно считать,
что температура
прогреваемого
цилиндра по
всему сечению
близка к одинаковой,
то есть равна
температуре
на поверхности
аппарата.
Величина
![]() может быть
найдена из
соответствующих
критериальных
зависимостей,
например, для
ламинарного
режима
может быть
найдена из
соответствующих
критериальных
зависимостей,
например, для
ламинарного
режима
![]() ,
,
где
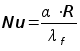 – критерий
Нуссельта,
– критерий
Нуссельта,
![]() –
теплопроводность
воздуха в печи,
–
теплопроводность
воздуха в печи,
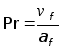 – критерий
Прандтля,
– критерий
Прандтля,
![]() – кинематическая
вязкость воздуха,
зависящая от
температуры,
– кинематическая
вязкость воздуха,
зависящая от
температуры,
![]() – температуропроводность
воздуха, зависящая
от температуры,
– температуропроводность
воздуха, зависящая
от температуры,
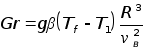 – критерий
Грасгофа,
– критерий
Грасгофа,
![]() – ускорение
свободного
падения,
– ускорение
свободного
падения,
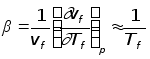 ,
,
![]() – средняя температура
воздуха в печи.
– средняя температура
воздуха в печи.
Для
оценочных
расчетов коэффициента
теплоотдачи
при свободной
конвекции на
вертикальной
поверхности
иногда используется
формула
![]() .
Оценим порядок:
пусть
.
Оценим порядок:
пусть
![]() и
и
![]() .
Примем температуру
воздуха в печи
порядка средней
между температурой
нагревателей
и аппарата:
.
Примем температуру
воздуха в печи
порядка средней
между температурой
нагревателей
и аппарата:
![]() .
тогда
.
тогда
![]() .
В выкладках,
приведенных
ниже, используется
именно эта
зависимость,
хотя, поскольку
интегрирование
приведенной
ниже системы
обыкновенных
дифференциальных
уравнений
возможно только
численными
методами, можно
применять и
более точные
методы определения
.
В выкладках,
приведенных
ниже, используется
именно эта
зависимость,
хотя, поскольку
интегрирование
приведенной
ниже системы
обыкновенных
дифференциальных
уравнений
возможно только
численными
методами, можно
применять и
более точные
методы определения
![]() .
Можно также
определить
.
Можно также
определить
![]() экспериментальным
путем и затем
использовать
эмпирическую
зависимость.
экспериментальным
путем и затем
использовать
эмпирическую
зависимость.
Зависимость
теплоемкости
вещества от
температуры,
как правило,
хорошо приближается
полиномами
1...2 степеней:
![]() .
.
Запишем уравнения теплового баланса для нагревателей печи, воздуха и аппарата:
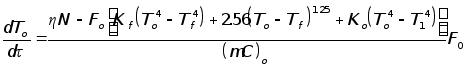
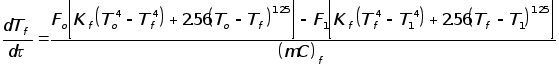
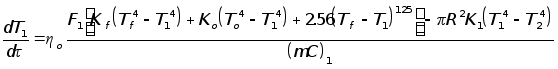
где![]() – средняя
теплоемкость
нагревателей,
воздуха или
аппарата, зависящая
от температуры
реакционной
смеси,
– средняя
теплоемкость
нагревателей,
воздуха или
аппарата, зависящая
от температуры
реакционной
смеси,
![]() – масса нагревателей
(1), воздуха(f)
или аппарата(o),
– масса нагревателей
(1), воздуха(f)
или аппарата(o),
![]() – мощность,
подводимая
к печи,
– мощность,
подводимая
к печи,
![]() – тепловой КПД
печи, определяемый
экспериментально.
– тепловой КПД
печи, определяемый
экспериментально.
Полученная система дифференциальных уравнений легко разрешается любым численным методом. Она достаточно устойчива, что позволяет поддерживать шаг интегрирования явным методом порядка 100 секунд.
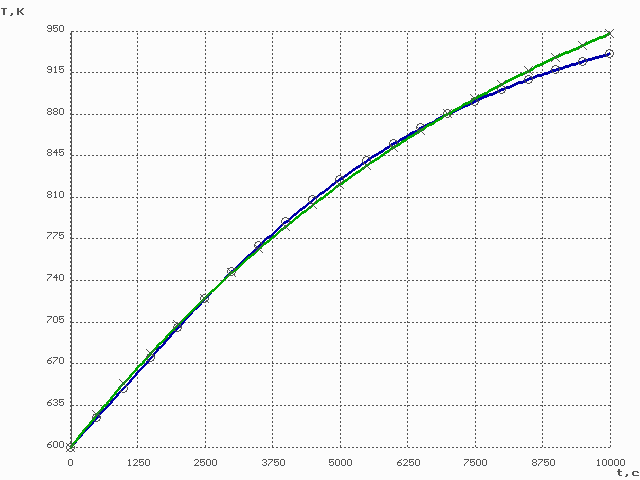
На
графике показана
зависимость
температуры
аппарата от
времени (при
условии отсутствия
кипения), полученная
решением системы
(О) при эффективной
подводимой
мощности
![]() кВт, и по эмпирическому
уравнению
кВт, и по эмпирическому
уравнению
![]() ,
,
где
![]() – заданная
температура,
– заданная
температура,
![]() = 0.4, аппроксимирующему
экспериментальные
данные.
= 0.4, аппроксимирующему
экспериментальные
данные.
Зависимость
давления паров
Mg и MgCl2 от температуры
хорошо приближается
формулой
![]() ,
где
,
где
![]() – эмпирические
коэффициенты,
или
– эмпирические
коэффициенты,
или
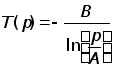 .
Для магния
.
Для магния
![]() ,
,
![]() ;
для MgCl2
;
для MgCl2
![]() ,
,
![]() .
Задаваясь
давлением в
аппарате, находим
температуру
кипения. Время
прогрева получим,
интегрируя
приведенную
выше систему
до момента,
когда температура
сравняется
с температурой
кипения магния
при заданном
давлении в
аппарате.
.
Задаваясь
давлением в
аппарате, находим
температуру
кипения. Время
прогрева получим,
интегрируя
приведенную
выше систему
до момента,
когда температура
сравняется
с температурой
кипения магния
при заданном
давлении в
аппарате.
Максимальная
температура,
до которой
можно прогревать
аппарат, определяется
исходя из скорости
взаимодействия
губки с материалом
реторты и лежит
в пределах
![]() К.
Имеет смысл
во время прогрева
препятствовать
началу кипения,
поддерживая
в аппарате
некоторое
давление. Так,
в указанном
интервале
температур
магний вскипает
при давлении
ниже 0.026...0.05 МПа.
Затем производится
сброс давления
до давления
сепарации
(10...100 Па), в результате
чего начинается
интенсивное
объемное кипение
по всему объему
аппарата. При
указанном выше
содержании
летучих компонентов
можно ожидать,
что силы поверхностного
натяжения будут
препятствовать
появлению
гидростатической
составляющей
давления в
объеме аппарата.
Можно оценить
количество
летучих, которые
выкипят за
время сброса
давления, исходя
из баланса
тепла:
К.
Имеет смысл
во время прогрева
препятствовать
началу кипения,
поддерживая
в аппарате
некоторое
давление. Так,
в указанном
интервале
температур
магний вскипает
при давлении
ниже 0.026...0.05 МПа.
Затем производится
сброс давления
до давления
сепарации
(10...100 Па), в результате
чего начинается
интенсивное
объемное кипение
по всему объему
аппарата. При
указанном выше
содержании
летучих компонентов
можно ожидать,
что силы поверхностного
натяжения будут
препятствовать
появлению
гидростатической
составляющей
давления в
объеме аппарата.
Можно оценить
количество
летучих, которые
выкипят за
время сброса
давления, исходя
из баланса
тепла:
![]() ,
,
где
![]() – удельная
теплота парообразования.
Окончательно
имеем
– удельная
теплота парообразования.
Окончательно
имеем
![]() .
.
Это уравнение имеет аналитическое решение
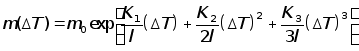 ,
,
где
![]() – начальная
масса летучих,
или при постоянной
теплоемкости
аппарата
– начальная
масса летучих,
или при постоянной
теплоемкости
аппарата
![]() .
.
где
![]() – изменение
температуры,
– изменение
температуры,
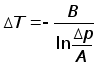 .
По окончании
объемного
кипения вся
реакционная
масса будет
иметь одинаковую
температуру
.
По окончании
объемного
кипения вся
реакционная
масса будет
иметь одинаковую
температуру
![]() .
.
Расчет по программе, реализующей приведенную выше методику, дает следующую зависимость массы летучих в аппарате от количества циклов нагрев – сброс давления:
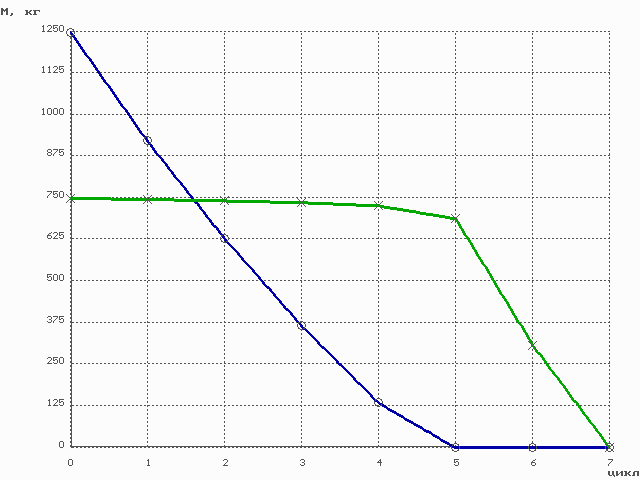
Таким образом, за 7 циклов теоретически возможно полностью удалить все летучие из аппарата.
Неясным является следующий вопрос: как распределяется тепло, аккумулированное аппаратом в процессе нагрева под давлением, между летучими? В приведенном расчете предполагалось, что количество поглощаемой на испарение теплоты пропорционально теплопроводности и количеству магния или хлористого магния в аппарате.
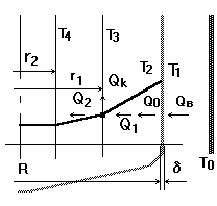
![]() ,
,
где
![]() – тепловой
поток, подводимый
к фронту,
– тепловой
поток, подводимый
к фронту,
![]() – тепло, расходуемое
на кипение,
– тепло, расходуемое
на кипение,
![]() – тепловой
поток, пропускаемый
фронтом.
– тепловой
поток, пропускаемый
фронтом.
Тепловой
поток
![]() считаем полностью
расходуемым
на испарение:
считаем полностью
расходуемым
на испарение:
![]()
или
![]() .
.
Будем
предполагать
квазистационарное
распределение
температур
в реакционной
массе. Это
справедливо,
если прогрев
происходит
достаточно
медленно (![]() ),
что доказано
выше. В этом
случае зависимость
температуры
от радиуса
цилиндра при
заданных граничных
условиях 1 рода
(температура
на внешней и
внутренней
поверхности)
выражается
формулой
),
что доказано
выше. В этом
случае зависимость
температуры
от радиуса
цилиндра при
заданных граничных
условиях 1 рода
(температура
на внешней и
внутренней
поверхности)
выражается
формулой
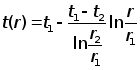 ,
,
где
![]() – текущий радиус,
– текущий радиус,
![]() – температура
наружной (горячей)
поверхности,
– температура
наружной (горячей)
поверхности,
![]() – температура
внутренней
(холодной)
поверхности,
– температура
внутренней
(холодной)
поверхности,
![]() – радиус наружной
(горячей) поверхности,
– радиус наружной
(горячей) поверхности,
![]() – радиус внутренней
(холодной)
поверхности,
– радиус внутренней
(холодной)
поверхности,
а удельный
линейный тепловой
поток в цилиндр
формулой
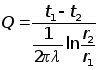 Вт/м.
Вт/м.
В
принятой модели
не рассматривается
теплообмен
блока с внешней
средой, кроме
подвода теплоты
от печи, поэтому
вся теплота
![]() (см. рис.) расходуется
на испарение
магния, а теплота
(см. рис.) расходуется
на испарение
магния, а теплота
![]() ,
расходуемая
на испарение
MgCl2, находится
из приведенных
выше зависимостей.
,
расходуемая
на испарение
MgCl2, находится
из приведенных
выше зависимостей.
Окончательно, получим систему уравнений для определения скоростей движения фронтов кипения:
![]() ;
;
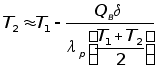 ;
;
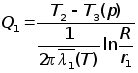 ;
;
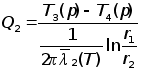 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
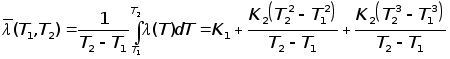 .
.
Интегрируя
эту систему
до тех пор, пока
![]() ,
находим время,
необходимое
для испарения
всех летучих.
,
находим время,
необходимое
для испарения
всех летучих.
Возможен и другой подход к расчету второй стадии. Можно предположить, что после интенсивного объемного кипения летучие не будут заполнять протяженные сплошные области, а распределятся по блоку “каплями”, не имея друг с другом хорошего теплового контакта. Тогда теплопроводность блока будет определяться исключительно теплопроводностью губки, и
![]()
и, соответственно,
![]() ;
;
![]() ;
;
![]()
Следовательно, нельзя принимать допущение, что температура блока по сечению постоянна. Используя формулу
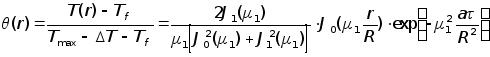 ,
,
справедливую
при больших
![]() ,
можно получить
зависимость
температуры
на оси цилиндра
от времени.
Температура
подогревающего
воздуха, в общем
случае, неизвестна,
но принимая
во внимание
большую продолжительность
процесса и
малое изменение
температуры
поверхности
аппарата на
2 стадии, можно
предположить,
что она приблизительно
равна температуре
нагревателей
печи. Недостаток
такого предположения
частично покрывается
тем, что в дальнейшем
выводе опущен
теплоподвод
излучением
от нагревателей
печи и подогревающего
воздуха.
,
можно получить
зависимость
температуры
на оси цилиндра
от времени.
Температура
подогревающего
воздуха, в общем
случае, неизвестна,
но принимая
во внимание
большую продолжительность
процесса и
малое изменение
температуры
поверхности
аппарата на
2 стадии, можно
предположить,
что она приблизительно
равна температуре
нагревателей
печи. Недостаток
такого предположения
частично покрывается
тем, что в дальнейшем
выводе опущен
теплоподвод
излучением
от нагревателей
печи и подогревающего
воздуха.
На
внешней поверхности
цилиндра (![]() )
имеем
)
имеем
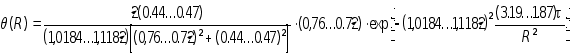
или
![]() .
.
Отсюда
можно получить
время прогрева
поверхности
до величины
![]() как
как
![]()
или
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
При
![]() имеем
имеем
![]() и
и
После
этого, по условиям
процесса, температура
у стенки аппарата
поддерживается
постоянной
и равной
![]() .
Изменение
температуры
на оси цилиндра
при граничных
условиях 1 рода
определяется
формулой
.
Изменение
температуры
на оси цилиндра
при граничных
условиях 1 рода
определяется
формулой
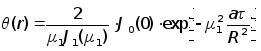 ,
,
или
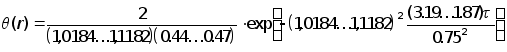 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таким образом, получены все необходимые и достаточные аналитические выражения для определения продолжительности процесса сепарации на 1 стадии и максимальной продолжительности 2 стадии при различных допущениях о характере процесса. Продолжительность 3 стадии (высокотемпературной выдержки) определяется по условию малости остатка летучих в объеме блока. Она зависит от объемного коэффициента теплопередачи от блока к каплям летучих и скорости их кипения (оба параметра неизвестны, и для них отсутствуют эмпирические зависимости), поэтому должна определяться экспериментально.
12