Реферат: Модель рассеяния электромагнитной волны параллелепипедом из диэлектрика с потерями

Содержание

Введение.........................................................................................................

Основные уравнения.....................................................................................

Фурье-компоненты рассеянной волны......................................................

Уравнения Виннера-Хопфа..........................................................................

Приближенные решения..............................................................................

Примеры расчетов и примеры экспериментов.........................................

Заключение....................................................................................................

МОДЕЛЬ РАССЕЯНИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ

ПАРАЛЛЕЛЕПИПЕДОМ ИЗ ДИЭЛЕКТИКА С ПОТЕРЯМИ.

ВВЕДЕНИЕ.

В настоящей статье изучается задача рассеяния плоской волны параллелепипедом из диэлектрика с потерями, причем считается, что размеры параллелепипеда сравнительно больше по отношению к длине волны. При исследовании используется метод Виннера-Хопфа. А именно, посредством обобщения решения задачи для полубесконечного тела, полученного в работе Джоунса, попытаемся распространить результаты для полубесконечных пластин из диэлектрика с большим потерями так же, как было получено решение для параллелепипеда из проводника. Само собой разумеется, что полученные результаты совпадают с решением для случая идеального проводника, если считать удельную электрическую проводимость бесконечно большой. В качестве характерной особенности предлагаемого метода, по-видимому, можно указать на то, что этот метод, так же как и метод в случае параллелепипеда из проводника, оказывается чрезвычайно эффективным в применении к телам с поперечным сечением в виде продолговатого прямоугольника, большая сторона которого сравнительно велика по отношению к длине волны. Конечно, в случае больших размеров тел приближение геометрической оптики и приближение физической оптики могут практически применяться в качестве наиболее простых методов, однако, для того, чтобы знать в каком диапазоне размеров эти приближения являются верными, необходимо выполнить точные расчеты и провести эксперименты. В данной работе приводятся также и результаты модельных экспериментов, в которых использовались микроволны; проведено сравнительное изучение с результатами расчетов. Что касается среды с большими потерями, то в параллелепипеде закреплялся бетон, а в качестве проводника использовалась алюминиевая пластина, изготовленная в виде параллелепипеда.

На рис.1 представлено схематическое изображение параллелепипеда и геометрические данные рассматриваемой задачи. В данном случае исследуется задача рассеяния (двухмерная) плоской волны (Е-волны), падающей на параллелепипед из диэлектрика с большими потерями под углом q к оси х. Ширина параллелепипеда равна 2а, толщина - 2b. Считаем, что изменение во времени описывается фактором .

Рис.1. Схематическое изображение данных задаче

ОСНОВНЫЕ УРАВНЕНИЯ.

Полное электромагнитное поле (t), рассеянная волна (S) и падающая волна (i) связаны следующим соотношением:

( 1 )

Считаем, что падающая плоская волна в рассматриваемой задаче может быть задана в следующем виде:

( 2 )

Здесь: , - диэлектрическая проницаемость и магнитная проницаемость в вакууме.

В силу строения рассеивающего тела (двухмерности задачи) плоскость поляризации неизменна, уравнения Максвелла можно записать в следующем виде:

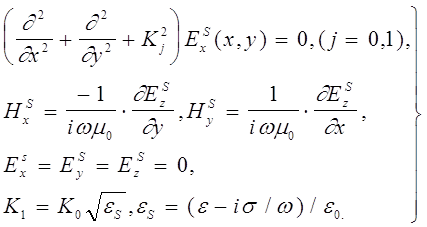(3)

Здесь индекс j=0 относится к волновому уравнению в вакууме, а j=1 - к волновому уравнению в среде с потерями. Кроме того, величины e, s представляют собой диэлектрическую проницаемость и удельную электрическую проводимость среды с потерями, обозначает комплексную относительную диэлектрическую проницаемость.

Решение уравнений (3) в данной задаче можно отыскивать так, чтобы удовлетворялись следующие граничные условия:

(В1) условия излучения вовне при r ® ¥ ;

(В2) непрерывность при | y |=b ;

(В3) непрерывность при | x |=a, | y |=b ;

(В4) непрерывность при | y |=b ;

(В5) условия концевой точки при | x |=a , | y |=b .

При решении задачи используется преобразование Фурье и обратное преобразование Фурье, которые определяются ниже следующим образом:

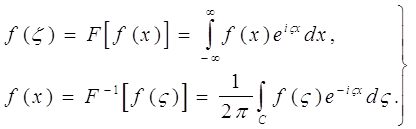(4)

Здесь контур интегрирования С в обратном преобразовании представляет собой контур интегрирования в интеграле с бесконечными пределами, находящийся в общей области Д¢ , которая может быть получена на основании предположения о том, что в вакууме имеются незначительные потери (JmK0<0) (область Д, не являющаяся общей, обусловлена существованием полюса z=z0, сопутствующего падающей волне).

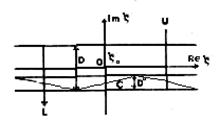
Рис.2. Плоскость комплексной переменной z и контур интегрирования С

ФУРЬЕ-КОМПОНЕНТЫ РАССЕЯНОЙ ВОЛНЫ

Для проведения исследования дальше разложим рассеянную волну на три электромагнитные волны следующим образом:

, (5)

причем считаем, что каждая электромагнитная волна при | y | £ b удовлетворяет следующим соотношениям:

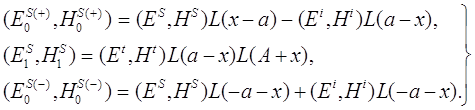(6)

Здесь: L(x) - ступенчатая функция:

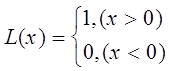(7)

Смысл индексов, которыми снабжены каждая из электромагнитных волн, как видно из формул (6), определяющих эти электромагнитные волны, заключается в следующем. Нижний индекс «0»соответствует тому, что поле удовлетворяет волновому уравнению в вакууме, а индекс «1» - тому, что поле удовлетворяет волновому уравнению в среде с потерями. Другими словами, эти индексы соответствуют значениям индекса j=0, 1 в уравнениях (3). Кроме того, верхний значок (+) указывает на то, что данное поле имеет смысл только при x >a, а значок (-) - на то, что рассматриваемое поле имеет смысл только при x <-a. В силу этих определений делаются особенно ясными аналитические свойства Фурье-компонент каждой электромагнитной волны и становится возможным выполнение исследования, основанного на теоретико-функциональных рассуждениях.

Найдем теперь Фурье-компоненты рассеянной волны. Прежде всего посредством перехода к прямому преобразованию Фурье в волновом уравнении (3) при | y | ³ b можно получить следующее уравнение:

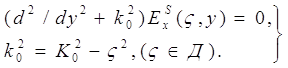(8)

Решение этого уравнения, удовлетворяющее граничным условиям (В1), (В2), может быть записано следующими образом:

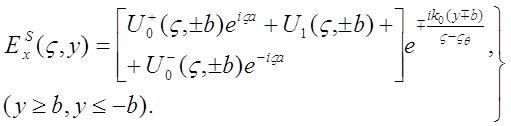(9)

Считаем здесь, что ветвление выбирается условием . Кроме того, неизвестные функции представляют собой, как показывают приводимые ниже формулы, Фурье-компоненты рассеянной волны при | y | = b. Наконец, точка представляет собой полюс, происходящий от падающей волны:

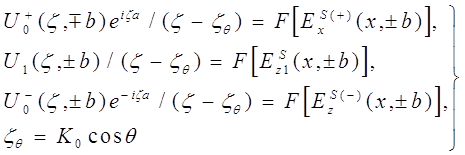(10)

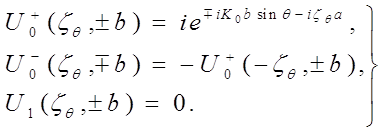(11)

Здесь значок справа у неизвестной функции указывает на то, что в случае значка «+» эта функция регулярна в верхней полуплоскости ( в области U ), а в случае значка « - » рассматриваемая функция регулярна в нижней полуплоскости ( в области L ). В дальнейшем используется этот способ обозначений.

С другой стороны, при | y | £ b существует разрыв в среде. В результате выполнения прямого преобразования Фурье в волновом уравнении (3) оно превращается в следующие дифференциальные уравнения неодинакового порядка:

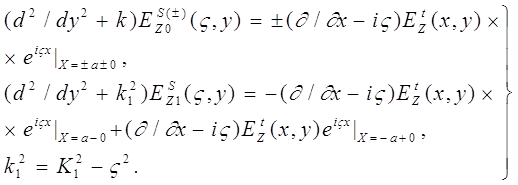(12)

Здесь «вынужденные» члены в правых частях можно вывести, принимая во внимание то обстоятельство, что величины в соотношениях (6) и падающая волна () непрерывны при | x | = a.

Из уравнений (3) следует, что представляет собой производную , умноженную на постоянный коэффициент, поэтому, полагая

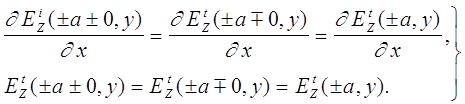(13)

можем добиться того, чтобы удовлетворялось граничное условие (В3). В приведенных соотношениях символ производной означает, что в производной выполнен предельный переход . Таким образом, разлагая волну на торцевой плоскости ( при | x | = a ) в следующий ряд, можем легко найти специальные решения уравнений (12):

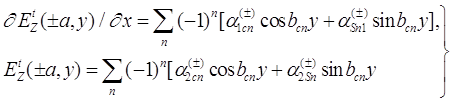(14)

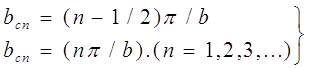(15)

Что касается соотношений (14), то они превращаются в специальный способ разложения в ряд Фурье. Иначе говоря, представляют собой разложения по системе ортогональных функций, превращающихся в нуль при | y | =b. Физически они представляют собой собственные колебания плоскопараллельного волновода. Достаточность таких разложений будет видна из обсуждения свойств регулярности, о которых речь идет ниже. Окончательно, в качестве решения уравнений (12), удовлетворяющих граничным условиям (В2), (В3), можем записать следующие выражения :

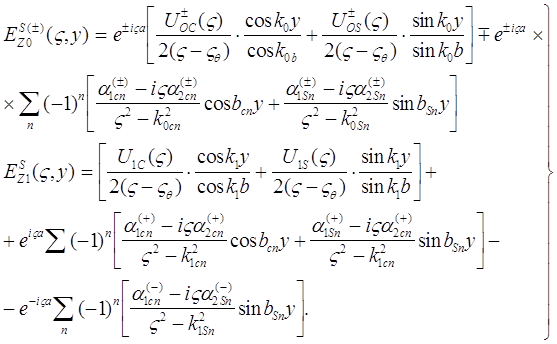(16

Здесь члены рядов представляют собой частные решения. Кроме того, неизвестные функции, снабженные нижними индексами C, S, представляют собой, с учетом свойств четности в соотношениях (10), следующие выражения ( j=0, 1):

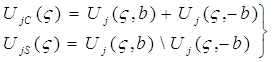(17)

Наконец, выполняются следующие соотношения ( j=0, 1, q= c, s):

(18)

В заключение обсудим коэффициенты разложений в формулах (14). Как отмечалось и при разъяснении формул (6), выступающих в качестве определений, за исключением членов, связанных с падающей волной (известные выражения), функция определена при x>a, а функция определена при x<-a. Это означает, что Фурье-компоненты этих функций обладают следующим свойствами регулярности, за исключением полюса при =q : компонента регулярна в верхней полуплоскости (области U), а компонента регулярна в нижней полуплоскости (области L). С другой стороны, функция определена на ограниченном интервале -a<x<b, так что ее Фурье-компонента представляет собой целую функцию. Конкретно, записывая в следующем виде

(19)

заметим, что регулярна в верхней полуплоскости, а регулярна в нижней полуплоскости. Функции в соотношениях (16) обладают свойствами регулярности, о которых говорилось здесь, поэтому коэффициенты разложений по формулам (14) не являются произвольными, а их нужно определять таким образом, чтобы исключить полюса в каждой полуплоскости. После выполнения необходимых преобразований коэффициенты могут быть заданы в следующем виде:

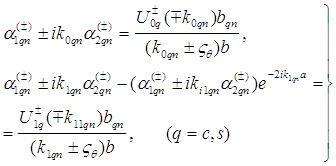(20)

Если допустить иные разложения, чем задаваемые формулами (14), то сохранение описанных здесь свойств регулярности становится невозможным. Таким образом ясно, что способ разложения по формулам (14) оказывается достаточным для рассматриваемой задачи.

УРАВНЕНИЯ ВИННЕРА-ХОПФА

В предыдущем разделе было установлено, что используя только Фурье-компоненты рассеянной волны (конкретно, ) на граничной плоскости | y |=b, можно представить Фурье-компоненты рассеянной волны в каждой из областей () таким образом, чтобы удовлетворялись граничные условия (В1), (В2), (В3). Таким образом, если в конечном счете удастся отыскать эти неизвестные Фурье-компоненты так, чтобы удовлетворить граничному условию (В4), то тем самым поставленная задача будет решена. Как следует из уравнений (3), граничное условие (В4) можно свести к непрерывности производной при | y |=b. Если записать это требование, используя формулы (9) и (16), то окончательный результат после выполнения необходимых преобразований, учитывающих свойства четности Фурье-компонент, может быть записан в следующем виде (q= c, s):

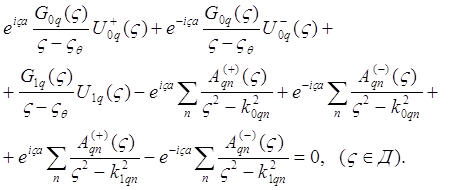(21)

Здесь кернфункции (ядра)задаются следующими формулами:

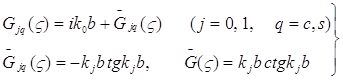(21)

(22)

Уравнения (21) по существу представляют собой систему уравнений Винера-Хопфа. Этот факт становится еще более очевидным, если применить преобразования по приводимым ниже формулам. А именно, если умножить эти уравнения на или , выполнить преобразования с использованием соотношений (19), то можно получить два следующих соотношения:

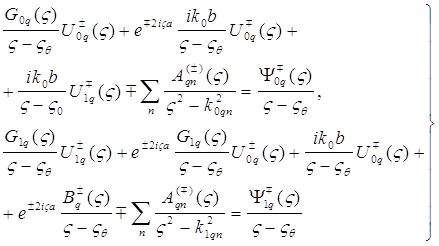(24)

При этом имеют место следующие соотношения:

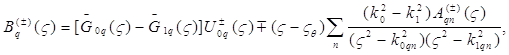(25)

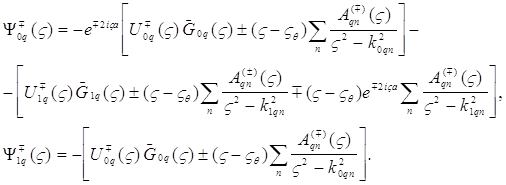(26)

Тот факт, что правые части в формулах (24), а в конечном счете, правые части в формулах (26), являются регулярными в верхней полуплоскости (области U ) или в нижней полуплоскости (области L ), можно установить следующим образом. Ясно, что с первого взгляда можно заключить, что особенностью функции являются только полюса в L. Однако, эти полюса исключаются в силу соотношений, представляемых формулой (20), так что эта функция оказывается регулярной в нижней полуплоскости. Аналогично, функция является регулярной в верхней полуплоскости.

Что касается системы уравнений Винера-Хопфа, представленной формулой (24), то ее решение можно найти, выполняя интегрирование вдоль разрезов от точек ветвления в разложениях керн-функций на множители. При выполнении расчетов возникают определенные затруднения, однако вывод решений проводится автоматически. Сначала выполняем разложение керн-функций на частное (произведение) функций, регулярных в верхней полуплоскости и в нижней полуплоскости, и, сверх того, не имеющих нулей (j=0, 1, q= c, s ):

(27)

Затем, делим (умножаем) правые части и левые части уравнений (24) на эти функции разложения, исключаем их полюса и выполняем интегрирование вдоль разрезов от точек ветвления. Если выполнить описанные действия, то обе части уравнений (24) можно разложить таким образом, что они окажутся регулярными соответственно в верхней полуплоскости (область U) или в нижней полуплоскости (область L). Более того, полученные соотношения окажутся справедливыми в общей области Д. Следовательно, по теореме Лиувилля обе части вместе оказываются функциями, регулярными во всей плоскости, т.е. постоянными. Однако, эти постоянные в силу граничного условия (В5) концевой точки, оказываются равными нулю, так что решение уравнений (24) определяется единственным образом. Здесь в качестве граничного условия концевой точки принимается условие -const при | x | ®a, | y |®b. Окончательный результат представляется в следующем виде:

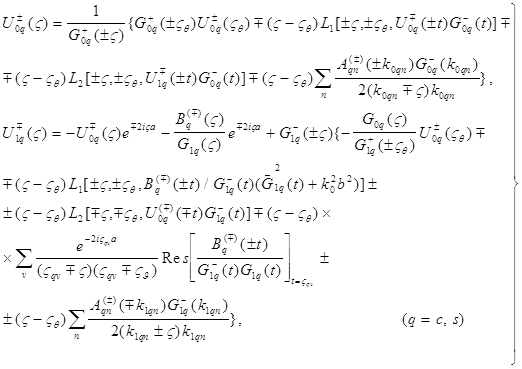(28) Здесь выражаются через интегралы вдоль разрезов от точек ветвления (рис. 3, 4). А именно, если считать, что функция регулярна в точках пути интегрирования то тогда определяются по формулам:

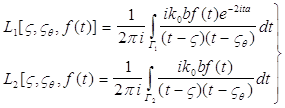(29)

Наконец, обозначают нули керн-функций, а Res - вычет.

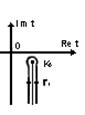
Рис.3. Путь интегрирования

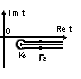
Рис.4. Путь интегрирования

(30)

N представляет собой число нулей в нижней полуплоскости. Эти нули соответствуют собственным значениям плоской волны вдоль пластины из диэлектрика с потерями толщины 2b, если интерпретировать их с физической точки зрения.

Формулы (28) представляют формальное решение на основании точного исследования. Если в этом решении перейти к пределу то а будет совпадать с решением для идеального проводника (подробности доказательства опускаются).

ПРИБЛИЖЕННЫЕ РЕШЕНИЯ

Рассмотрим приближенные решения для случая, когда в среде имеются потери, а ширина прямоугольного цилиндра велика по сравнению с длиной волны. Если считать, что в диэлектрике имеются потери, а ширина прямоугольного цилиндра 2а мала, то можем положить:

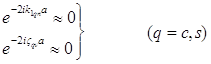(31)

Если выполнять расчеты для бетона , используя полученные к настоящему времени данные на основании экспериментальных результатов, то даже в диапазоне ультравысоких частот при ширине в одну длину волны абсолютные величины в (31) ниже . Отсюда следует, что можно пренебречь экспоненциальными членами в соотношениях (20) и членами, связанными с плоской волной, в соотношениях (28), если ширина 2а больше длины волны. Это означает, что почти можно пренебречь взаимодействием рассеянных волн на обеих торцевых плоскостях (x= a и x= -a), обусловленных электромагнитной волной, распространяющейся в среде с потерями, и плоской волной, возбужденной в пластине из диэлектрика с потерями, поскольку затухание вследствие потерь велико. Кроме того, функциональные величины необходимо определять алгебраически посредством подстановки в формулы (28), но и в этом случае можно пренебречь всеми экспоненциальными членами. Следовательно, выполнение расчетов в среде с потерями, в качестве которой предполагается бетон, значительно упрощается.

Рассмотрим далее интегралы вдоль разрезов от точек ветвления, а именно, оценим интегралы (29). Интеграл представляет собой величину, характерную для задачи с конечной шириной; если ширина 2а мала, то путем выбора пути интегрирования так, чтобы он был параллелен мнимой оси, оценку можно получить по методу наибыстрейшего спуска. С другой стороны, интеграл является величиной характерной для полубесконечной пластины из диэлектрика. В этом случае интеграл можно найти аналитически, если выбрать путь интегрирования параллельным действительной оси и предположить, что подынтегральная функция такова, что к ее регулярной части применимо приближение ломаными линиями.

Выполняя расчеты численно с использованием описанных выше методов приближения, можно сравнительно просто отыскать неизвестные Фурье-компоненты. Переходя в полученных результатах к обратному преобразованию Фурье, можем найти рассеянную волну. В частности, ограничиваясь дальнейшей рассеянной волной и используя преобразование переменных x= r cos j, y= r sin j и метод перевала, можно легко выполнить необходимые расчеты.

ПРИМЕРЫ РАСЧЕТОВ И ПРИМЕРЫ ЭКСПИРИМЕНТОВ

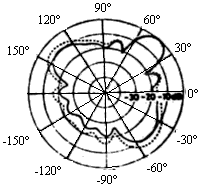
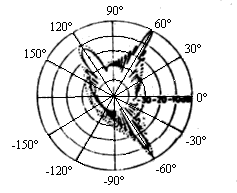
На рис.5,6 приведены примеры, в которых найдены дальние рассеянные волны при помощи использования приближенных методов, описанных в предыдущем разделе. На приведенных рисунках значения представлены нормированными на максимальное значение в дБ. Результаты, изображенные сплошными линиями относятся к диэлектрику с потерями, а изображенные пунктирными линиями - к идеальному проводнику. Значение представляет один из примеров измеренного значения комплексной относительной диэлектрической проницаемости бетона при частоте 100 МГц. Размеры рассеивающих тел, результаты для которых приведены на рис.5, порядка длины волны ( 2l х 2l), а на рис.6 - сравнительно большие по отношению к длине волны (приблизительно 13l х 12l), однако, общим для обоих рисунков является то, что на теневой стороне нет различий между средой с большими потерями и идеальным проводником. Ясно, что отраженная волна подавляется средой с потерями.

Рис.5. Дальняя рассеянная волна (дБ):

1 диэлектрик с большими потерями; 2 идеальный проводник

Рис.6. Дальняя рассеянная волна (дБ)

1 диэлектрик с большими потерями; 2 идеальный проводник.

Для подтверждения результатов численных расчетов были выполнены модельные эксперименты с использованием микроволн частоты 15 ГГц. Упрощенное изображение экспериментального оборудования, установленного в помещении, изолированном от влияния электрических волн, показано на рис.7. Излучающая пирамидоидальная рупорная антенна, центр рассеивающего тела (конечной длины) и приемная пирамидоидальная рупорная антенна устанавливались в одной и той же горизонтальной плоскости. Излучающая антенна находилась в фиксированном положении, приемная антенна могла передвигаться по рельсам, проложенным по окружности с центром на центральной оси рассеивающего тела. При этом расстояние между центральной осью рассеивающего тела и излучающей антенной составляет 3 м. (150 l).

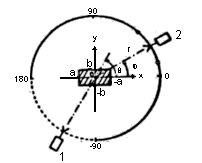
Рис.7. Оборудование для измерения рассеянной волны:

1 - передатчик (излучающая антенна); 2 - приемник (приемная антенна)

То обстоятельство, что при выполнении сравнения экспериментальных результатов и результатов численных расчетов следует соблюдать определенную осторожность, связано с тем, что в экспериментах происходит интерференция падающей и рассеянной волн позади рассеивающего тела и измерение только рассеянной волны с технической точки зрения сопряжено со значительными трудностями. Одним из методов является выполнение сравнения только с отраженной волной. Однако, в данной работе в качестве одной из попыток решено провести сравнение с волной, которая получается в результате умножения падающей плоской волны на весовую функцию:

(33)

При этом функция f(j) представляет собой функцию, которая зависит от приемопередающих характеристик измерительной системы, а именно от угла, под которым происходит прием в электрическом поле принимаемых сигналов приемной антенной при отсутствии рассеивающего тела. В данной работе используется аппроксимация этой функции тригонометрическими функциями так, чтобы при отклонении от точки на одной прямой с передающим рупором больше, чем ± 30° происходило ослабление на - 20 дБ.

На рис.8 представлены измеренные и рассчитанные значения для рассеянной волны в том случае, когда параллелепипед из бетона с поперечным сечением в виде квадрата (25,5 см. х 25,5 см.) облучается электрической волной при угле падения 60°. При этом максимум в рассчитанных значениях равен 0 дБ, а измеренные значения представляют собой значения, которые сопоставляются рассчитанным значениям через максимальный уровень отраженной волны. Использованное в расчетах значение комплексной относительной диэлектрической проницаемости представляет собой значение, найденное по методу кратковременного открытия (short×open) с заполнением микроволнового волновода на 15 ГГц бетоном. Это значение, будучи сравнено с результатами измерений, выполненных другими исследователями, представляется правильным.

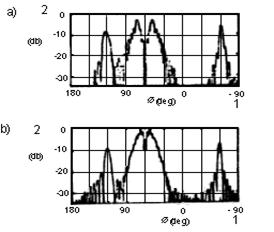
Из рис.8 видно, что измеренные значения и рассчитанные значения для отраженной волны хорошо согласуются. С другой стороны, в теневой области (30°-90°) обнаруживаются и чрезвычайно отчетливые различия в этих значениях. В качестве первой причины этих различий можно указать на то обстоятельство, что падающая волна не является плоской волной в реальных экспериментах, а близка к сферической волне. Заключение об этом можно с делать так же и по тому факту, что, вследствие распространения фронта волны, в измеренных значениях более всего проявляется теневая темная часть. В качестве второй

Рис.8. рассеянная волна на диэлектрике с большими потерями: а) - результаты измерений (бетон); b) - результаты расчетов (при ); 1 - Æ(град); 2 - (дБ).

В качестве второй причины можно считать то обстоятельство, что описанная экспериментальная система не является вполне двухмерной моделью. В экспериментах в качестве параллелепипеда используется тело конечной длины (1 м.), установленное на подставке; это приводит к тому, что нельзя пренебрегать влиянием волны, отраженной от подставки. Эти влияния проявляются в заметной интерференции измеренных значений при 10° - 110°. В качестве других причин можно отметить, что рассеянная волна в формуле (33) представляет собой величину, полученную применением просто метода перевала, вряд ли являющуюся хорошим приближением.

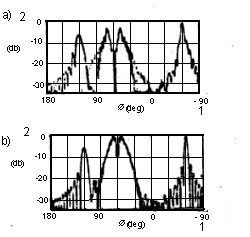
Для изучения различий между бетоном и проводником на рис.9 приводится пример результатов для случая , когда рассеивающее тело заменено на проводник с теми же параметрами, что и на рис.8. Измеренные значения относятся к случаю алюминиевой пластины толщиной 1 мм., изготовленной для параллелепипеда, а рассчитанные значения относятся к случаю идеального проводника. И в этом примере обнаруживается, что измеренные значения для отраженной волны и рассчитанные значения хорошо согласуются. Кроме того очевидно, что предположение о том, идеальным проводником является даже алюминиевая пластина, оказывается достаточно правильным. Наконец, сравнивая рис.8, 9, можем заключить, что подавление отраженной волны наблюдается в среде с большими потерями. Это заключение совпадает с заключением, сделанном на основании рис.5, 6.

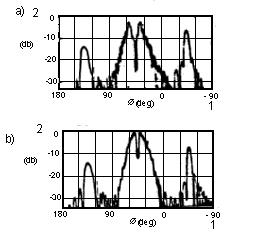
На рис.10 представлены результаты, которые относятся к случаю, когда ширина равна ширине рассеивающего тела, приведенной на рис.8, а толщина в два раза меньше; угол падения выбран равным 45°. Очевидно, что в той мере, насколько мала толщина, отраженная волна в направлении j= 135° слабее волны, отраженной под углом j= -45°. И в этом примере измеренные значения для отраженной волны хорошо согласуются с рассчитанными значениями.

Рис.9. Рассеянная на проводнике волна: а) - результаты измерений (алюминий);

b) - результаты расчетов (идеальный проводник); 1 - Æ (град.); 2 - (дБ).

Рис.10. Рассеянная волна диэлектриком с большими потерями: а) - результаты измерений (бетон); b) - результаты расчетов (при ); 1 - Æ (град.); 2 - (дБ)

ЗАКЛЮЧЕНИЕ

Приведена точная формулировка задачи рассеяния плоской электромагнитной волны (Е-волны) на параллелепипеде из диэлектрика с большими потерями, в которой используется преобразование Фурье. В терминах преобразований Фурье приведено решение задачи. В том случае, когда ширина рассеивающего тела сравнительно велика по отношению к длине волны, а в среде этого тела имеются большие потери порядка потерь в бетоне, как показывает исследование, расчеты можно значительно упростить. Обсуждены различия по сравнению со случаем идеального проводника.