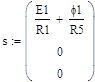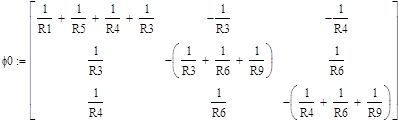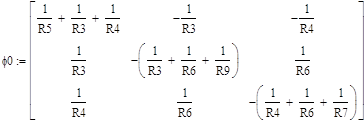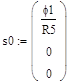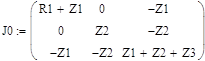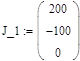Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология и педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по информатике программированию
Краткое содержание произведений
Реферат: Электроника и электротехника
Реферат: Электроника и электротехника
Курсовое
расчётно-графическое задание
по курсам: ”Электротехника”
“Электротехника и электроника”
1. Расчёт электрической цепи постоянного тока
 |
Исходные данные:
 E1 R1 I1 j2 I3 R3
E1 R1 I1 j2 I3 R3
R5 R4
E2 I2 I5 I4 I6 R6
j1 j5 j3
I8 I7
R8 R7
I9 R9
j4
1.1. Расчёт токов во всех ветвях схемы методом узловых потенциалов
Пусть j1,j2,j3,j4,j5 – потенциалы (j4=0),
I1, I2, I3, I4, I5, I6, I7, I8, I9 – токи в соответствующих участках цепи.
 |
По 2-му закону Кирхгоффа:
Для данной расчётной схемы составим матрицу, использовав метод узловых потенциалов :
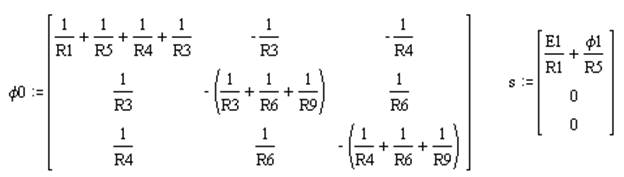 |
Откуда:
Для отдельных участков цепи, согласно 2-му закону Кирхгоффа, запишем:
 |
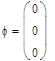
Для узла 1 запишем 1-ый закон Кирхгоффа:
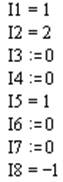 |
Получили:
1.2. Проверка расчёта токов по уравнению баланса мощности
Мощность источника:
Мощность потребителя:
Тогда:
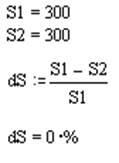 |
Мощность источника отличается от мощности потребителя, на 0 %.
1.3.
![]() Построение потенциальной диаграммы для контура 1-2-3-4
Построение потенциальной диаграммы для контура 1-2-3-4
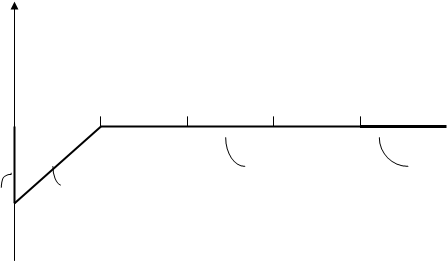
j
2 3 4
0 R R
j3 j4
j1 j2
1
1.4. Определение тока в ветви с E1 методом эквивалентного генератора

E1 R1 I1 j2 R3
a b
1 Uxx
E1 R5 R4 R6
j1 I5 j5 j3
![]() j4 R8
R7 R9
j4 R8
R7 R9
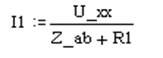 |
, где Uxx - напряжение холостого хода, Z_ab - входное сопротивление
По 2-му закону Кирхгоффа для контура 1:
 |
для участка цепи 1-4:
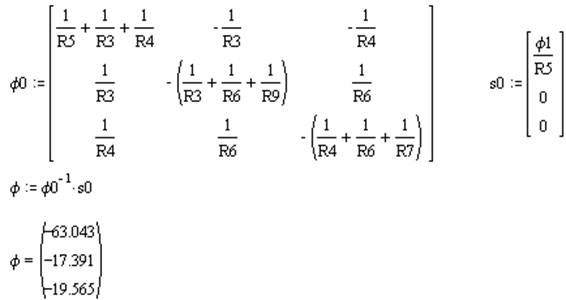 |
j2 – найдём, используя метод узловых потенциалов:
Откуда
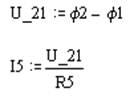 |
Тогда для участка цепи 1-2:
Следовательно:
Найдём z_ab:
R3
 a b
a b
R5 R4 R6
R8 R7 R9
Треугольник с сопротивлениями R3, R4, R6 преобразуем в треугольник:

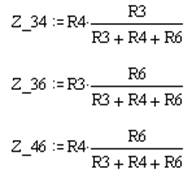 |
Z_34
a b
R5
Z_46 Z_36
R7 R9
R8
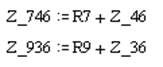 |
Сопротивления Z_46 и R7, Z_36 и R9 соединены последовательно:
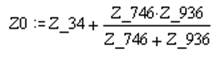 |
Полученные сопротивления соединены параллельно, а сопротивление Z_34 соединено с ними последовательно:
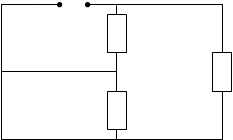 a b
a b
R5
Z0
R8
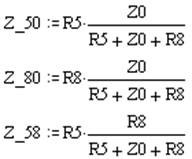 |
Полученный треугольник с сопротивлениями R5, R8, Z0 преобразуем в звезду:
 a b
a b
Z_50
Z_58
Z_80
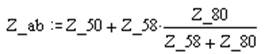 |
Тогда:
Следовательно, получим:
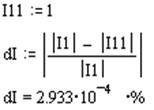 |
Где I11-ток в цепи с E1, полученный методом узловых потенциалов.
Ток, полученный методом эквивалентного генератора, отличается от тока, полученного методом узловых потенциалов, на 2.933*10-4%, что вполне допустимо.
2. Расчёт электрической цепи синусоидального тока
Исходные данные :
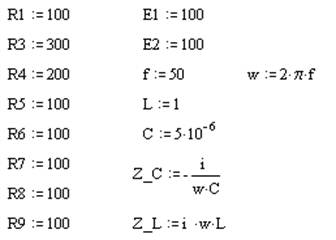


 E1
R1 R3
E1
R1 R3
 |
|||||
 |
 |
||||
R5 R4
![]()
![]()
![]()
![]()
![]()
![]()
![]() E2 XC
R6 XL
E2 XC
R6 XL
![]()
![]()
R8 R7 R9
![]()
2.1 Преобразование электрической цепи к 3-х ячеистой схеме.
Сопротивления Z_L и R6 соединены последовательно, тогда :
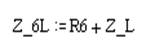
E1 R1 R3
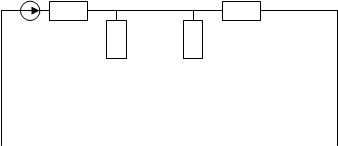
R5 R4
![]()
![]() E2 Z_C
Z_6L
E2 Z_C
Z_6L
R8 R7 R9
![]()
Преобразуем звезду с сопротивлениями R3,R9,Z_6L в треугольник :

![]()
![]() E1 R1
E1 R1
 |
|||
 |
|||
R5 R4 Z_01
![]()
![]()
![]()
![]()
![]() E2 Z_C
E2 Z_C
![]()
![]()
![]()
![]()
![]() Z_03
Z_03
R8 R7 Z_02
![]()
 |
Пары сопротивлений R4 с Z_01 и R7 с Z_02 соединены последовательно, следовательно:
E1 R1
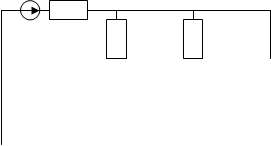
R5 Z_04
![]()
![]()
![]() E2 Z_C
E2 Z_C
![]()
![]()
![]()
![]()
![]()
![]() Z_03
Z_03
R8 Z_05
![]()
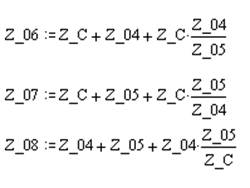 |
Преобразуем звезду с сопротивлениями Z_C,Z04,Z05 в треугольник :
![]()
![]() E1 R1
E1 R1
 |
|||
 |
|||
R5 Z_06





 E2
E2
![]()
![]()
![]() Z_08 Z_03
Z_08 Z_03
R8 Z_07
![]()
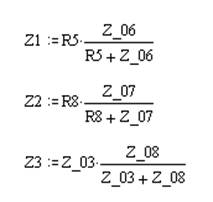
Пары сопротивлений R5 с Z_06 , R8 с Z_07 , Z_08
с Z_03 соединены последовательно, следовательно:
E1 R1 I1
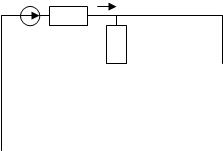 |
|||
![]() J1 Z1
I3
J1 Z1
I3
![]()
![]()
![]()
![]() E2 I4
E2 I4
![]()
![]()
![]()
![]()
![]() J3
Z3
J3
Z3
![]()
![]()
![]()
![]() I2 I5
I2 I5
J2 Z2
![]()
Получили преобразованную 3-х ячеистую схему
2.2 Определение токов (действующих в ветвях преобразованной схемы) методом контурных токов.

Запишем искомые токи через контурные:
Составим матрицу для контурных токов:

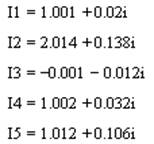 |
Найденные токи будут следующие:
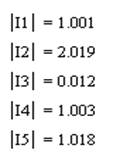 |
Абсолютное значение которых, равно:
2.3 Проверка расчёта токов по уравнению баланса мощности
Мощность источника:
 |
Мощность потребителя:
Мощность источника отличается от мощности потребителя, на 0.035%, что вполне допустимо.
2.4 Векторная диаграмма токов во всех ветвях преобразованной эл. Схемы
[R]=Ом ; [Z]=Ом; [E]=В; [f]=Гц; [L]=Г; [С]=Ф; [I]=А; [S]=Вт.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1_2. Расчет эл. цепи методом эквивалентного генератора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2. Расчет эл. цепи синусоидального тока |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|