Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология и педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по информатике программированию
Краткое содержание произведений
Реферат: Метрология, стандартизация и сертификация
Реферат: Метрология, стандартизация и сертификация
 Московский автомобильно-дорожный институт
Московский автомобильно-дорожный институт
(государственный технический университет)
Кафедра: Строительство и эксплуатация дорог.
Курсовая работа
по дисциплине:
«Метрология, стандартизация и сертификация»
Выполнил: Проверил:
Группа 3ВАП4 Преподаватель
Молчанов Д.Н. Жустарева Е.В.
Москва
2003 год
Содержание.
Часть 1: Организация статистического контроля качества дорожно-строительных работ.
Часть 2: Статистическая обработка результатов измерений:
1) определение статистических характеристик выборки;
2) определение абсолютных и относительных погрешностей, оценка влияния числа измерений на точность определяемых статистических характеристик;
3) интервальная оценка параметров распределения;
4) исключение результатов распределения;
Часть 3: Проверка гипотезы о подчинении выборки нормальному закону распределения.
Часть 1
Организация статистического контроля качества строительных работ.
Определение необходимого числа измерений.
Дорога 2-й категории, модуль упругости грунта II
Необходимое минимальное достаточное число измерений
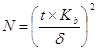 где,
где,
t – нормированное отклонение
Kb – коэффициент вариации
d - относительная погрешность
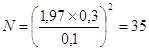
Составляем схему.
Bуч – 15м
Lуч – 200м
Нормированное отклонение (t) – 1,97
Kb – 0,30
d - 0,1
Выбираем 35 случайных чисел и наносим их на схему участка измерений, затем для сокращения в объёме работ из них выберем 5 и найдём их координаты.
Значения:
86; 51; 59; 07; 04; 66; 15; 47; 64; 72; 56; 62; 8; 53; 32; 94; 39; 76; 78; 02; 69; 18; 60; 33; 93; 42; 50; 29; 92; 24; 88; 95; 55; 37; 34.
|
|
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|
||||
|
|
22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
|
||||
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |
|
||||
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |
|
||||
|
|
82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
![]()
|
Вывод: для контроля модуля упругости на автомобильной дороге 2-й категории необходимо провести 35 измерений. Схема участка измерения представлена на рис.1. Координаты точек измерений следующие:
1) x1=55; y1=1,5
2) x2=105; y2=7,5
3) x3=65; y3=13,5
4) x4=55; y4=1,5
5) x5=145; y5=1,5
2. Определение необходимого числа измерений.
Дорога 2-й категории, модуль упругости грунта III
Необходимое минимальное достаточное число измерений
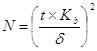 где,
где,
t – нормированное отклонение
Kb – коэффициент вариации
d - относительная погрешность
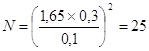
Составляем схему.
Bуч – 12м
Lуч – 200м
Нормированное отклонение (t) – 1,65
Kb – 0,30
d - 0,1
Выбираем 25 случайных чисел и наносим их на схему участка измерений, затем для сокращения в объёме работ из них выберем 5 и найдём их координаты.
Значения:
56; 46; 8; 53; 32; 94; 37; 76; 78; 02; 69; 18; 60; 33; 93; 42; 50; 29; 92; 24; 88; 95; 55; 84; 3.
|
|
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|
||||
|
|
22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
|
||||
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |
|
||||
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |
|
||||
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
![]()
![]()
|
Вывод: для контроля поперечного уклона на автомобильной дороге 2-й категории необходимо провести 25 измерений. Схема участка измерения представлена на рис.1. Координаты точек измерений следующие:
1) x1=155; y1=7,5
2) x2=145; y2=7,5
3) x3=65; y3=13,5
4) x4=125; y4=7,5
5) x5=115; y5=10,5
Часть 2
Статистическая обработка
результатов измерений.
2.1. Определение основных статистических характеристик выборки.
N = 20
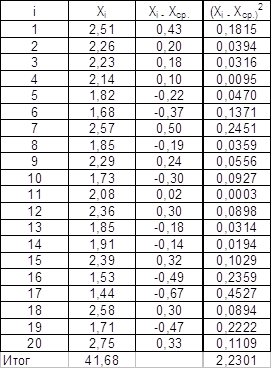 2.1.1. Размах
2.1.1. Размах
![]()
![]() 1,31
1,31
2.1.2. Среднее арифметическое значение
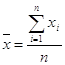
![]()
2.1.3. Среднее квадратичное отклонение
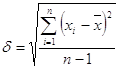
![]()
2.1.4. Дисперсия
![]()
![]()
2.1.5. Коэффициент вариации
![]()
![]()
0,1644>0,15 – неоднородная выборка
2.2. Определение основных статистических характеристик выборки.
N = 10
2.2.1. Размах
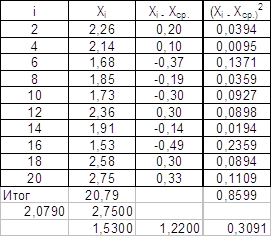
![]()
![]() 1,22
1,22
2.2.2. Среднее арифметическое значение
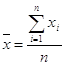
![]()
2.2.3. Среднее квадратичное отклонение
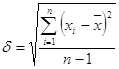
![]()
2.2.4 Дисперсия
![]()
![]()
2.2.5. Коэффициент вариации
![]()
![]()
0,1487<0,15 - однородная выборка
2.3. Определение основных статистических характеристик выборки.
N = 5
2.3.1. Размах
![]()
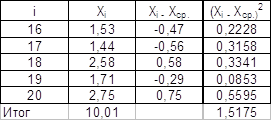
![]() 1,31
1,31
2.3.2. Среднее арифметическое значение
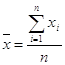
![]()
2.3.3. Среднее квадратичное отклонение
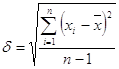
![]()
2.3.4 Дисперсия
![]()
![]()
2.3.5. Коэффициент вариации
![]()
![]()
0,3076>0,15 - неоднородная выборка
2.4. Определение абсолютной и относительной погрешностей выборки. Оценка влияния числа измерений на точность определения статистических характеристик.
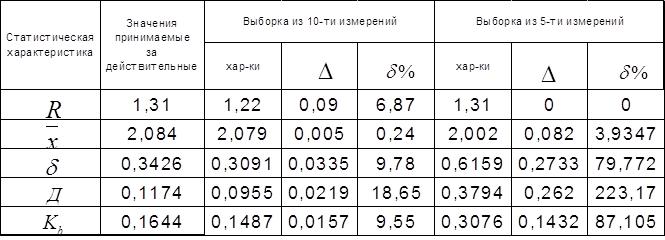
Вывод: При выборке N=10 среднеарифметическое значение имеет низкую погрешность, остальные значения погрешностей достаточно высоки (более 5%). При выборке N=5 среднеарифметическое значение также имеет низкую погрешность, остальные значения погрешностей высоки (более 50%), а дисперсия более 100%. В целом, можно заключить, что при N=10 меньших процент погрешностей, чем при N=5.
Учитывая вышеизложенное, можно сказать, что с увеличением числа измерений точность определения характеристик возрастает, как следствие, погрешности уменьшаются.
Контрольная карта N = 5
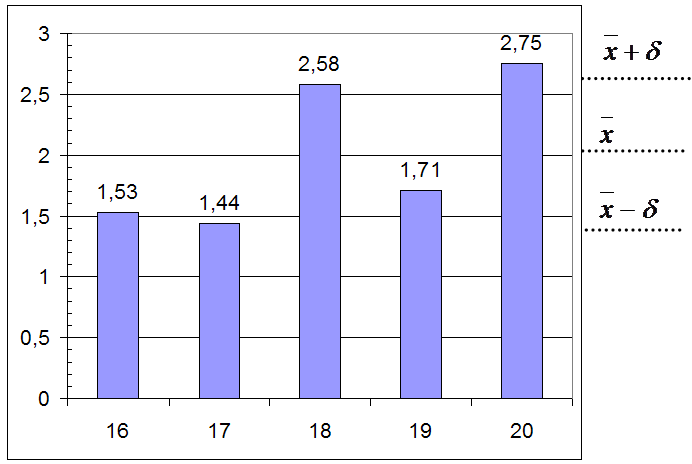
Контрольная карта N = 10
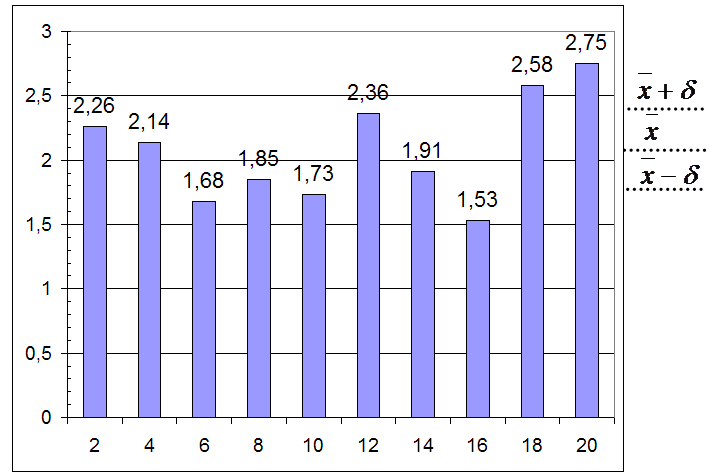
Контрольная карта N = 20
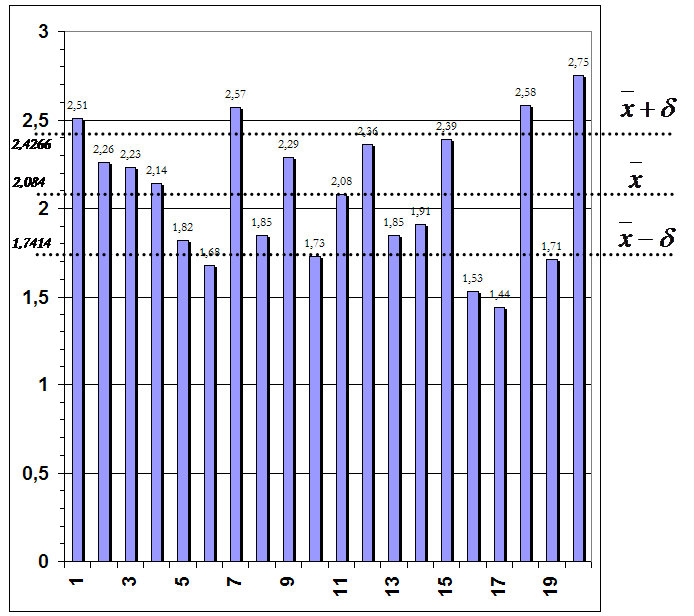
3. Интервальная оценка параметров распределения.
1. Определить границы доверительного интервала для
единичного результата измерения по формуле ![]() для
N = 20 для всех уровней Pдов.
для
N = 20 для всех уровней Pдов.
![]()
![]()
![]()
![]()
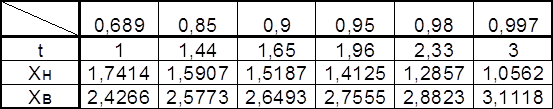
2. Построить кривую ![]() .
.
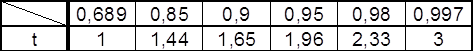
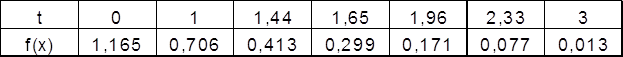
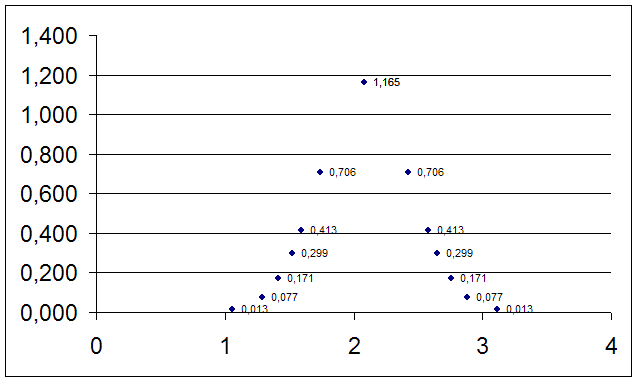
3. Определить границы доверительного интервала для истинного значения
![]() для N=20; 10; 5 для всех уровней Pдов.
для N=20; 10; 5 для всех уровней Pдов.
![]()
![]()
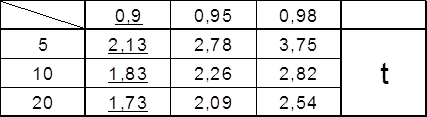
![]()
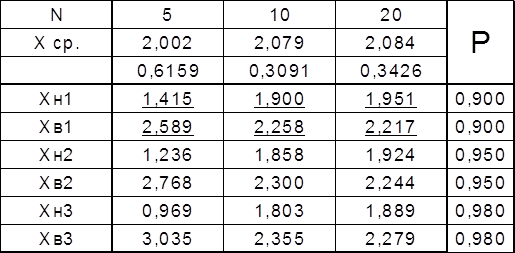
 4. Графически изобразить
интервалы для N=20; 10; 5 при Pдов.
= 0,9
4. Графически изобразить
интервалы для N=20; 10; 5 при Pдов.
= 0,9
Вывод: С уменьшением количества измерений границы доверительного интервала раздвигаются (для истинного значения случайной величины).
5. Исключение результатов, содержащие грубые погрешности.
Выборку из 20-ти измерений проверить на наличие результатов с погрешностями
методом «![]() ».
».
X20=2,084 Xmax = 2,75
![]() Xmin=1,44
Xmin=1,44
t=3
Pдов.=0,997
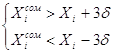
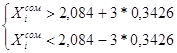
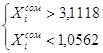
![]()
Неравенства являются верными, следовательно, в данной выборке (N=20) нет величин, содержащих грубую погрешность
2. Проверить выборки из 5-ти и 10-ти измерений на наличие результатов в погрешностями по методу Романовского для 3-х уровней доверительной вероятности. Определить при каком уровне доверительной вероятности появляется необходимость корректировать выборку.
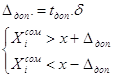 Для N=10
Для N=10 ![]()
![]()
![]()
![]()
Для N=5
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
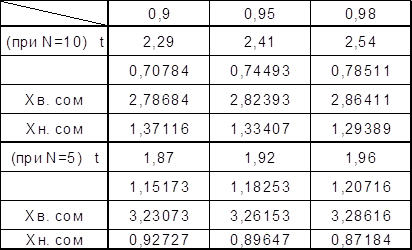
Вывод: в выборках при N=10; 5 нет значений, содержащих грубую погрешность, следовательно нет необходимости в корректировке данных при всех уровнях доверительной вероятности Pдов.
Часть 3
Проверка гипотезы о подчинении выборки нормальному закону распределения.
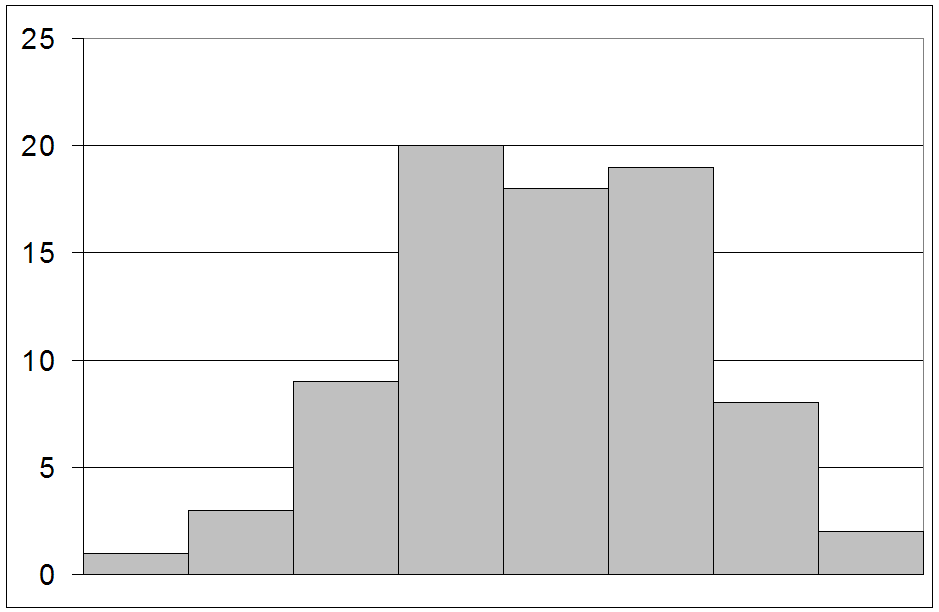
1. Построение гистограммы экспериментальных данных.
![]()
2. Построение теоретической кривой.
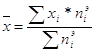
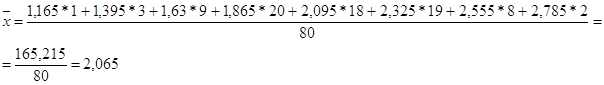
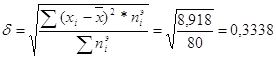
3. Вычисление
![]()
4. Оценка согласия экспериментальных и теоретических данных
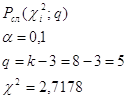
при ![]()
при![]()
Вывод: Гипотеза не отвергается, т.к. существует большая вероятность того, что расхождение между теоретическими и экспериментальными данными - случайность, обусловленная недостатком числа измерений или недостаточной точностью измерений.
| Интервал | Границы интервала |
Середина интервала
|
Частота
|
|
|
|
|
|
|
|
||||
| Нижняя | Верхняя | |||||||||||||
| 1 | 1,05 | 1,28 | 1,165 | 1 | -0,900 | 0,810 | 2,70 | 0,01 | 0,551 | 0,449 | 0,365 | |||
| 2 | 1,28 | 1,51 | 1,395 | 3 | -0,670 | 1,347 | 2,01 | 0,051 | 2,811 | 0,189 | 0,013 | |||
| 3 | 1,51 | 1,75 | 1,63 | 9 | -0,435 | 1,703 | 1,30 | 0,164 | 9,040 | -0,040 | 0,000 | |||
| 4 | 1,75 | 1,98 | 1,865 | 20 | -0,200 | 0,800 | 0,60 | 0,325 | 17,915 | 2,085 | 0,243 | |||
| 5 | 1,98 | 2,21 | 2,095 | 18 | 0,030 | 0,016 | 0,09 | 0,393 | 21,663 | -3,663 | 0,619 | |||
| 6 | 2,21 | 2,44 | 2,325 | 19 | 0,260 | 1,284 | 0,78 | 0,275 | 15,159 | 3,841 | 0,973 | |||
| 7 | 2,44 | 2,67 | 2,555 | 8 | 0,490 | 1,921 | 1,47 | 0,116 | 6,394 | 1,606 | 0,403 | |||
| 8 | 2,67 | 2,9 | 2,785 | 2 | 0,720 | 1,037 | 2,16 | 0,029 | 1,599 | 0,401 | 0,101 | |||
Сумма |
80 | 8,918 | 2,7178 | |||||||||||
|
|
1,7312 | 1,00 | 0,229 | 12,623 | ||||||||||
|
|
2,065 | 0,00 | 0,398 | 21,939 | ||||||||||
|
|
2,3988 | 1,00 | 0,229 | 12,623 | ||||||||||
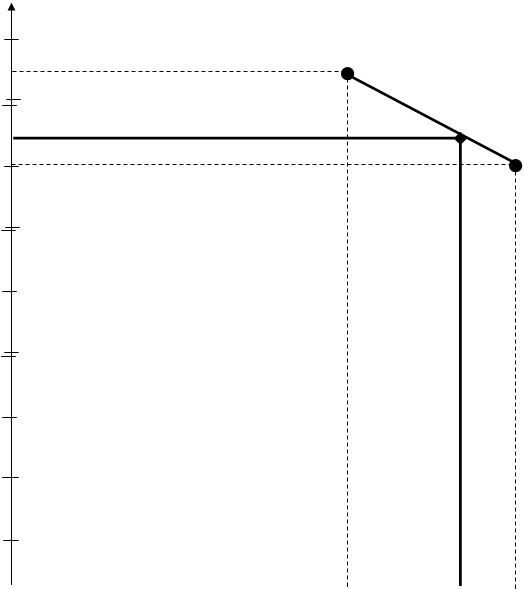 |
|||