
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология и педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по информатике программированию
Краткое содержание произведений
Реферат: Экономическое планирование методами математической статистики
Реферат: Экономическое планирование методами математической статистики
Министерство образования Украины
Харьковский государственный технический университет радиоэлектроники
Кафедра ПОЭВМ
Комплексная курсовая работа
по курсу «Вероятностные процессы и математическая статистика в автоматизированных системах»
Тема: «Провести экономическую оценку эффективности работы предприятия. Провести долгосрочное планирование работы методами прогнозирования. Построить математическую модель повышения эффективности работы».
Выполнил:
ст. гр. ПОВТАС-96-3 Наумов А.С.
Руководитель: асс. Шамша Т. Б.
Комиссия: проф. к. т. н. Дударь З. В.
проф. к. .т. н. Лесная Н. С.
асс. Шамша Т.Б.
1999
РЕФЕРАТ
Пояснительная записка к комплексной курсовой работе: 19 с., 2 рис.,
9 табл., 2 приложения,4 источника.
Цель задания – произвести статистический анализ исходных данных, полученных при исследовании основных показателей деятельности предприятия, с целью выявления доминирующих факторов влияющих на прибыль и построения адекватной математической модели для изучения возможностей ее максимизации и прогнозирования на последующие периоды.
Работа посвящена исследованию экономической деятельности предприятия методами статистического анализа. В качестве исходных данных принимается некоторая совокупность выборок по экономическим показателям, в частности прибыли, затратах, ценах и т.д. за некоторый отчетный период работы предприятия. В работе к этому набору данных применяются различные методы статистического анализа, направленные на установление вида зависимости прибыли предприятия от других экономических показателей. На основании полученных результатов методами регрессионного анализа построенна математическая модель и оценена ее адекватность. Помимо этого проведен временной анализ показателей прибыли за 4 года и выявлены закономерности изменения прибыли по месяцам. На основании этих данных проведено прогнозирование прибыли на следующий (текущий) год.
Работа выполнена в учебных целях.
РЕГРЕССИОННЫЙ
АНАЛИЗ, МНОЖЕСТВЕННАЯ
ЛИНЕЙНАЯ РЕГРЕССИЯ,
УРОВЕНЬ ЗНАЧИМОСТИ,
КРИТЕРИЙ СЕРИЙ,
КРИТЕРИЙ ИНВЕРСИЙ,
КРИТЕРИЙ
![]() ,
ВРЕМЕННЫЕ
РЯДЫ, МУЛЬТИПЛИКАТИВНО-АДИТИВНАЯ
МОДЕЛЬ, ТРЕНД.
,
ВРЕМЕННЫЕ
РЯДЫ, МУЛЬТИПЛИКАТИВНО-АДИТИВНАЯ
МОДЕЛЬ, ТРЕНД.
СОДЕРЖАНИЕ
Введение 4
Постановка задачи . 5
2. Предварительный анализ исходных данных……………………………8
3. Построение математической модели …………………… ……………..12
4. Временной анализ и прогнозирование………………………………….14
Выводы………………………………………………………………………16
Перечень ссылок. .17
Приложение А График зависимости колебаний прибыли предприятия
от времени……………………………………………………………… …..18
Приложение Б График прогноза изменения прибыли по месяцам……..19
ВВЕДЕНИЕ
Не вызывает сомнения тот факт, что организация любого производства без тщательного теоретического обоснования, экономических расчетов и прогнозирования – это растраченные впустую средства. Еще 10 лет назад такая подготовка занимала большое количество времени и средств, поскольку требовала значительного персонала и вычислительных мощностей. В настоящее время уровень развития вычислительной техники позволяет производить сложные статистические исследования при минимальных затратах рабочего времени, персонала и средств, что сделало их доступными для бухгалтерии каждого предприятия.
Безусловно, в условиях рыночной экономики, главным показателем рентабельности предприятия является прибыль. Поэтому очень важно понять, как необходимо вести хозяйство, что бы как говориться «не вылететь в трубу». И здесь незаменимы методы математической статистики, которые позволяют правильно оценить, какие факторы, и в какой степени влияют на прибыль, а так же на основании правильно построенной математической модели, спрогнозировать прибыль на будущий период.
1 ПОСТАНОВКА ЗАДАЧИ
Цель курсового проекта - сформировать профессиональные умения и навыки применения методов математической статистики к практическому анализу реальных физических процессов.
Цель задания – произвести статистический анализ исходных данных, полученных при исследовании основных показателей деятельности предприятия, с целью выявления доминирующих факторов влияющих на прибыль и построения адекватной математической модели для изучения возможностей ее максимизации и прогнозирования на последующие периоды.
Исходные данные для первой части поставленного задания приведены в табл. 1.1
Таблица 1.1 – Исходные данные для регрессионного анализа.
|
Прибыль |
Коэффициент качества продукции |
Доля в общем объеме продаж |
Розничная цена |
Коэффициент издержек на 1 продукции |
Удовлетворение условий розничных торговцев |
|
| № |
Y, % |
X1 |
X2 |
X3 |
X4 |
X5 |
|
1 |
1,99 |
1,22 |
1,24 |
1,3 |
35,19 |
2,08 |
|
2 |
12,21 |
1,45 |
1,54 |
1,04 |
80 |
1,09 |
|
3 |
23,07 |
1,9 |
1,31 |
1 |
23,31 |
2,28 |
|
4 |
24,14 |
2,53 |
1,36 |
1,64 |
80 |
1,44 |
|
5 |
35,05 |
3,41 |
2,65 |
1,19 |
80 |
1,75 |
|
6 |
36,87 |
1,96 |
1,63 |
1,26 |
68,84 |
1,54 |
|
7 |
4,7 |
2,71 |
1,66 |
1,28 |
80 |
0,47 |
|
8 |
58,45 |
1,76 |
1,4 |
1,42 |
30,32 |
2,51 |
|
9 |
59,55 |
2,09 |
2,61 |
1,65 |
80 |
2,81 |
|
10 |
61,42 |
1,1 |
2,42 |
1,24 |
32,94 |
0,59 |
|
11 |
61,51 |
3,62 |
3,5 |
1,09 |
28,56 |
0,64 |
|
12 |
61,95 |
3,53 |
1,29 |
1,29 |
78,75 |
1,73 |
|
13 |
71,24 |
2,09 |
2,44 |
1,65 |
38,63 |
1,83 |
|
14 |
71,45 |
1,54 |
2,6 |
1,19 |
48,67 |
0,76 |
Продолжение таблицы 1.1
|
15 |
81,88 |
2,41 |
2,11 |
1,64 |
40,83 |
0,14 |
|
16 |
10,08 |
3,64 |
2,06 |
1,46 |
80 |
3,53 |
|
17 |
10,25 |
2,61 |
1,85 |
1,59 |
80 |
2,13 |
|
18 |
10,81 |
2,62 |
2,28 |
1,57 |
80 |
3,86 |
|
19 |
11,09 |
3,29 |
4,07 |
1,78 |
80 |
1,28 |
|
20 |
12,64 |
1,24 |
1,84 |
1,38 |
31,2 |
4,25 |
|
21 |
12,92 |
1,37 |
1,9 |
1,55 |
29,49 |
3,98 |
Основная цель первой части задания оценить влияние на прибыль предприятия от реализации продукции одного вида следующих факторов:
Х1 - Коэффициент качества продукции;
Х2 - Доля в общем объеме продаж;
Х3 – Розничная цена продукции;
Х4 – Коэффициент издержек на единицу продукции;
Х5 – Удовлетворение условий розничных торговцев.
Необходимо, применив регрессионные методы анализа, построить математическую модель зависимости прибыли от некоторых (или всех ) из вышеперечисленных факторов и проверить адекватность полученной модели.
На следующем этапе работы исходными данными являются суммы прибыли предприятия (конкретнее – завода шампанских вин) по каждому месяцу за четыре года, которые представлены в табл. 1.2.
Таблица 1.2 – Исходные данные для временного анализа
|
Месяц |
1994 |
1996 |
1997 |
1998 |
|
Январь |
1500000 |
1650000 |
1400000 |
1700000 |
|
Февраль |
900000 |
850000 |
890000 |
1200000 |
|
Март |
700000 |
600000 |
550000 |
459000 |
|
Апрель |
300000 |
125000 |
250000 |
221000 |
|
Май |
400000 |
300000 |
100000 |
1000 |
|
Июнь |
250000 |
450000 |
150000 |
250000 |
Продолжение таблицы 1.2
|
Июль |
200000 |
600000 |
132000 |
325000 |
|
Август |
150000 |
750000 |
142000 |
354000 |
|
Сентябрь |
300000 |
300000 |
254000 |
150000 |
|
Октябрь |
250000 |
259000 |
350000 |
100000 |
|
Ноябрь |
400000 |
453000 |
450000 |
259000 |
|
Декабрь |
2000000 |
1700000 |
1000000 |
1900000 |
На этом этапе необходимо провести анализ имеющихся данных методами временных рядов, что позволит выявить закономерности колебаний прибыли по месяцам (цикличность и сезонность этих колебаний). Исследование этой закономерности позволит спрогнозировать прибыль на следующий год.
Предварительный анализ исходных данных.
Прежде чем применить к имеющимся у нас исходным данным метод регрессионного анализа, необходимо провести некоторый предварительный анализ имеющихся в нашем распоряжении выборок. Это позволит сделать выводы о качестве имеющихся в нашем распоряжении данных, а именно: о наличии или отсутствии тренда, нормальном законе распределения выборки, оценить некоторые статистические характеристики и т.д.
Для всех последующих расчетов примем уровень значимости 0.05, что соответствует 5% вероятности ошибки.
2.1 Исследование выборки по прибыли.
Математическое ожидание (арифметическое среднее) 582791,6667.
Доверительный интервал для математического ожидания (429399,2878; 736184,0456).
Дисперсия (рассеивание) 2,78993E+11.
Доверительный интервал для дисперсии (2,78993E+11; 5,36744E+11).
Средне квадратичное отклонение (от среднего) 528197,6018.
Медиана выборки 352000.
Размах выборки 1999000.
Асимметрия (смещение от нормального распределения) 1,372426107.
Эксцесс выборки (отклонение от нормального распределения)
0,795776027.
Коэффициент вариации (коэффициент представительности среднего) 91%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в табл. 2.1 (2-й столбец). Сумма серий равняется 10. Поскольку данное значение не попадает в доверительный интервал (табличные значения) от 18 до 33, следовательно, гипотеза о статистической независимости и отсутствии тренда не подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в табл. 2.1 (3-й столбец). Сумма инверсий равняется 585. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 495 до 729, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 2.1 – Критерии серий и инверсий
|
Прибыль |
Критерий серий |
Критерий инверсий |
|
1500000 |
+ |
42 |
|
900000 |
+ |
1 |
|
700000 |
+ |
34 |
|
300000 |
- |
18 |
|
400000 |
- |
24 |
|
250000 |
- |
11 |
|
200000 |
- |
9 |
|
150000 |
- |
6 |
|
300000 |
- |
15 |
|
250000 |
- |
9 |
|
400000 |
- |
19 |
|
2000000 |
+ |
36 |
|
1650000 |
+ |
32 |
|
850000 |
+ |
27 |
Продолжение таблицы 2.1
|
600000 |
+ |
24 |
|
125000 |
- |
3 |
|
300000 |
- |
13 |
|
450000 |
- |
17 |
|
600000 |
+ |
21 |
|
750000 |
+ |
21 |
|
300000 |
- |
13 |
|
259000 |
- |
11 |
|
453000 |
- |
16 |
|
1700000 |
+ |
22 |
|
1400000 |
+ |
21 |
|
890000 |
+ |
18 |
|
550000 |
- |
17 |
|
250000 |
- |
8 |
|
100000 |
- |
1 |
|
150000 |
- |
4 |
|
132000 |
- |
2 |
|
142000 |
- |
2 |
|
254000 |
- |
5 |
|
350000 |
- |
7 |
|
450000 |
- |
8 |
|
1000000 |
+ |
9 |
|
1700000 |
+ |
10 |
|
1200000 |
+ |
9 |
|
459000 |
- |
8 |
|
221000 |
- |
3 |
|
1000 |
- |
0 |
|
250000 |
- |
2 |
|
325000 |
- |
3 |
|
354000 |
- |
3 |
|
150000 |
- |
1 |
|
100000 |
- |
0 |
|
259000 |
- |
0 |
|
1900000 |
+ |
0 |
Из результатов анализа видно, что критерии серий и инверсий дают противоречивые результаты проверки наличия тренда. Следует учитывать, что критерий инверсий является более мощным для выявления линейного тренда, однако для выявления флуктуации предпочтение следует отдать критерию инверсий. Из вышесказанного можно предположить, что в выборке присутствует тренд, не являющийся, однако линейным, а скорее выраженный в виде флуктуации. Последующие исследования подтверждают данное предположение, что явно видно из графика представленного в приложении А.
Проверка гипотезы о нормальном законе распределения выборки с применением критерия
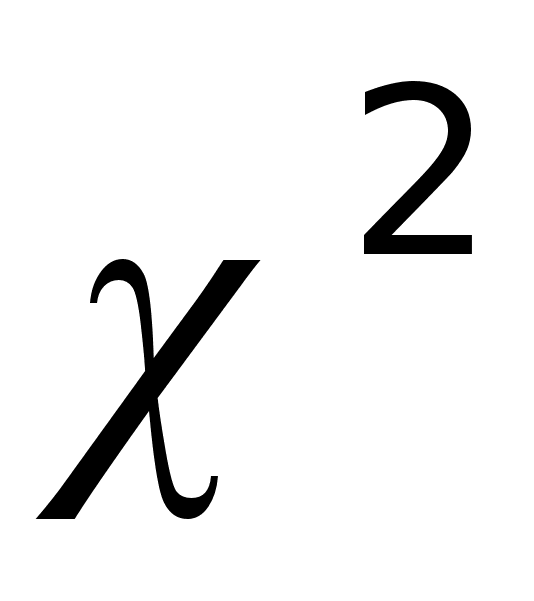 .
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
211279,0407.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=9.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в табл. 2.2.
.
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
211279,0407.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=9.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в табл. 2.2.
Таблица
2.2 – Критерий
![]() .
.
|
Интервалы группировки |
Расчетная частота |
Теоретическая частота |
|
212279,0407 |
10 |
2,8347E-05 |
|
423558,0815 |
17 |
3,46434E-05 |
|
634837,1222 |
7 |
3,60783E-05 |
|
846116,163 |
2 |
3,20174E-05 |
|
1057395,204 |
4 |
2,42124E-05 |
|
1268674,244 |
1 |
1,56028E-05 |
|
1479953,285 |
1 |
8,56803E-06 |
|
1691232,326 |
2 |
4,00933E-06 |
|
1902511,367 |
3 |
1,59873E-06 |
Результирующее значение критерия 0 значительно меньше табличного 55,70 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
3. Построение математической модели.
. Регрессионный анализ.
Для построения математической модели выдвинем гипотезу о наличии линейной зависимости между прибылью и фактором времени, на нее влияющим. Следовательно, математическая модель может быть описана уравнением вида:
![]() ,
(3.1)
,
(3.1)
где
![]() - линейно-независимые
постоянные
коэффициенты.
- линейно-независимые
постоянные
коэффициенты.
Для их отыскания применим регрессионный анализ. Результаты регрессии сведены в табл. 3.2 – 3.4.
Таблица 3.2 – Регрессионная статистика
|
Множественный R |
0,096181456 |
|
|
R-квадрат |
0,009250873 |
|
|
Нормированный R-квадрат |
-0,012287152 |
|
|
Стандартная ошибка |
537056,4999 |
|
|
Наблюдения |
48 |
|
Таблица 3.3. –Дисперсионная таблица
|
df |
SS |
MS |
F |
Значимость F |
|
|
Регрессия |
1 |
1,23884E+11 |
1,23884E+11 |
0,429513513 |
0,515492131 |
|
Остаток |
46 |
1,32678E+13 |
2,8843E+11 |
||
|
Итого |
47 |
1,33916E+13 |
Таблица 3.4 – Коэффициенты регрессии.
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|
|
Y |
672637,41 |
157489,387 |
4,27100 |
9,65555E-05 |
355628 |
989646, |
355628 |
989646 |
|
X |
-3667,1732 |
5595,55298 |
-0,65537 |
0,51549 |
-14930,4 |
7596,07 |
-14930,4 |
7596,07 |
Таким образом, уравнение, описывающее математическую модель, приобретает вид:
Y= 672637,4113-3667,173252X1. (3.2)
F-критерий из табл. 3.3 показывает степень адекватности, полученной математической модели.
4. Временной анализ и прогнозирование.
По условию задания необходимо проанализировать прибыль предприятия за четыре года его работы, и на основе полученных данных построить прогноз на пятый год. Для решения поставленной задачи воспользуемся методом временных рядов.
Для расчета сезонных индексов зададимся мультипликативно-аддитивной моделью тренда:
Y=kX+b, (4.1)
и, используя метод простой линейной регрессии, построим гипотетическую модель (Приложение А). Отклонения от модели, выраженные в процентах, представлены в табл. 4.1.
Таблица 4.1 – Отклонение от модели
|
1994 |
1996 |
1997 |
1998 |
|
|
Январь |
224% |
264% |
241% |
317% |
|
Февраль |
135% |
137% |
154% |
225% |
|
Март |
106% |
97% |
96% |
87% |
|
Апрель |
46% |
20% |
44% |
42% |
|
Май |
61% |
49% |
18% |
0% |
|
Июнь |
38% |
74% |
27% |
48% |
|
Июль |
31% |
100% |
24% |
63% |
|
Август |
23% |
125% |
26% |
69% |
|
Сентябрь |
47% |
50% |
46% |
30% |
|
Октябрь |
39% |
44% |
64% |
20% |
|
Ноябрь |
63% |
77% |
83% |
52% |
|
Декабрь |
318% |
291% |
185% |
383% |
Для того чтобы рассчитать прогноз на следующий год, рассчитаем сезонные индексы по табл. 4.1, а затем, по уравнению тренда, найдем теоретические значения прибыли на следующий год. Для получения окончательного прогноза проведем нормирование, умножив значения тренда на сезонные индексы. Значения расчетов приведены в табл. 4.2.
Таблица 4.2 – Результаты прогноза.
|
Сезонные индексы |
Тренд |
Прогноз на 1999 |
|
|
Январь |
209% |
492946 |
1031069 |
|
Февраль |
130% |
489279 |
637311 |
|
Март |
77% |
485612 |
374399 |
|
Апрель |
30% |
481944 |
146354 |
|
Май |
26% |
478277 |
122574 |
|
Июнь |
37% |
474610 |
177951 |
|
Июль |
43% |
470943 |
204531 |
|
Август |
49% |
467276 |
227353 |
|
Сентябрь |
35% |
463609 |
160283 |
|
Октябрь |
33% |
459941 |
153419 |
|
Ноябрь |
55% |
456274 |
250688 |
|
Декабрь |
235% |
452607 |
1064985 |
График прогнозируемой прибыли представлен в Приложении Б.
ВЫВОДЫ
В результате проведенной работы был произведен статистический анализ исходных данных, полученных при исследовании основных показателей деятельности предприятия, с целью выявления доминирующих факторов влияющих на прибыль и построена адекватная математическая модель и спрогнозирована прибыль на последующие периоды.
В процессе выполнения работы изучили и научились применять на практике следующие методы математической статистики:
линейный регрессионный анализ,
множественный регрессионный анализ,
корреляционный анализ,
проверка стационарности и независимости выборок,
метод временных рядов,
выявление тренда,
критерий
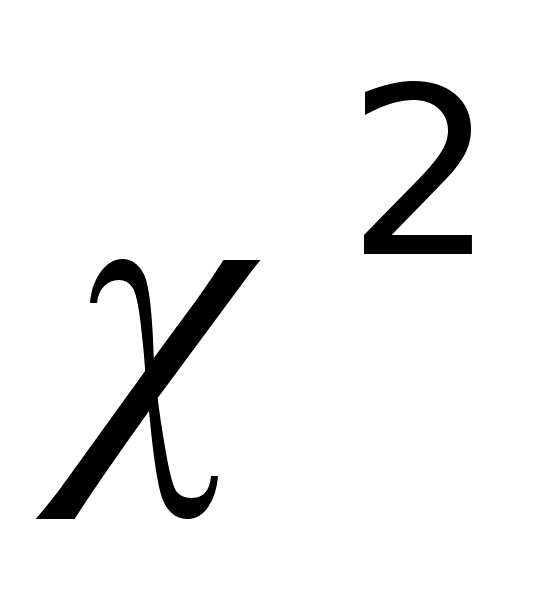 .
.
Перечень ссылок
Бендод Дж., Пирсол А. Прикладной анализ случайных данных: Пер. с англ. – М.: Мир, 1989.
Математическая статистика. Под ред. А. М. Длина, М.: Высшая школа, 1975.
Л.Н.Большев, Н.В.Смирнов. Таблицы математической статистики.-М.: Наука, 1983.
Н.Дрейпер, Г.Смит. Прикладной регрессионный анализ. Пер. с англ.- М.: Статистика, 1973.
ПРИЛОЖЕНИЕ А
Г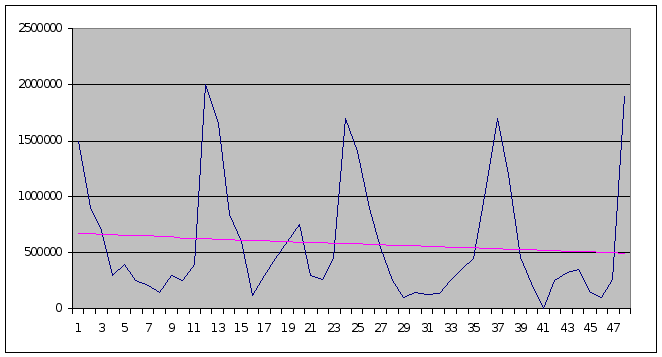
рафик
зависимости
колебаний
прибыли предприятия
от времени.
Рисунок А.1 – График зависимости прибыли предприятия от времени.
ПРИЛОЖЕНИЕ Б
График прогноза изменения прибыли по месяцам.
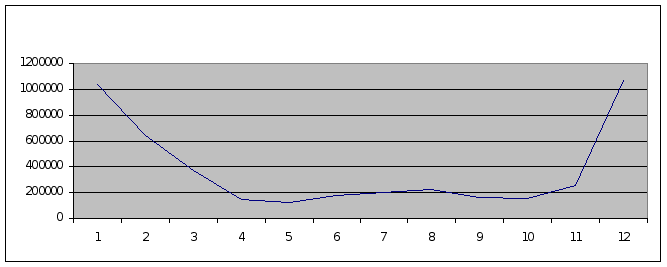
Рисунок Б.1 – График прогноза изменения прибыли по месяцам.
УДК
КП
Министерство образования Украины
Харьковский государственный технический университет радиоэлектроники
Кафедра ПОЭВМ
Комплексная курсовая работа
по курсу «Вероятностные процессы и математическая статистика в автоматизированных системах»
Тема: «Провести экономическую оценку эффективности работы предприятия. Провести долгосрочное планирование работы методом множественной линейной регрессии. Построить математическую модель повышения эффективности работы».
Выполнил:
Ст. гр. ПОВТАС-96-3 Фурсов Я. А.
Руководитель: асс. Шамша Т. Б.
Комиссия: проф. к. т. н. Дударь З. В.
проф. к.. т. н. Лесная Н. С.
асс. Шамша Т. Б.
1999
РЕФЕРАТ
Пояснительная записка к комплексной курсовой работе: 30 с.,
17 табл., 4 источника.
Цель задания – произвести статистический анализ исходных данных, полученных при исследовании основных показателей деятельности предприятия, с целью выявления доминирующих факторов влияющих на прибыль и построения адекватной математической модели для изучения возможностей ее максимизации и прогнозирования на последующие периоды.
Работа посвящена исследованию экономической деятельности предприятия методами статистического анализа. В качестве исходных данных принимается некоторая совокупность выборок по экономическим показателям, в частности прибыли, затратах, ценах и т.д. за некоторый отчетный период работы предприятия. В работе к этому набору данных применяются различные методы статистического анализа, направленные на установление вида зависимости прибыли предприятия от других экономических показателей. На основании полученных результатов методами регрессионного анализа построенна математическая модель и оценена ее адекватность. Помимо этого проведен временной анализ показателей прибыли за 4 года и выявлены закономерности изменения прибыли по месяцам. На основании этих данных проведено прогнозирование прибыли на следующий (текущий) год.
Работа выполнена в учебных целях.
МАТЕМАТИЧЕСКАЯ
МОДЕЛЬ, РЕГРЕССИОННЫЙ
АНАЛИЗ, МНОЖЕСТВЕННАЯ
ЛИНЕЙНАЯ РЕГРЕССИЯ,
УРОВЕНЬ ЗНАЧИМОСТИ,
КРИТЕРИЙ СЕРИЙ,
КРИТЕРИЙ ИНВЕРСИЙ,
КРИТЕРИЙ
![]() ,
ТРЕНД
,
ТРЕНД
СОДЕРЖАНИЕ
Введение 4
Постановка задачи 5
2.Предварительный анализ исходных данных……………………………7
3. Построение математической модели…………………………………….24
Выводы……………………………………………………………………….29
Перечень ссылок .30
ВВЕДЕНИЕ
Не вызывает сомнения тот факт, что организация любого производства без тщательного теоретического обоснования, экономических расчетов и прогнозирования – это растраченные впустую средства. Еще 10 лет назад такая подготовка занимала большое количество времени и средств, поскольку требовала значительного персонала и вычислительных мощностей. В настоящее время уровень развития вычислительной техники позволяет производить сложные статистические исследования при минимальных затратах рабочего времени, персонала и средств, что сделало их доступными для бухгалтерии каждого предприятия.
Безусловно, в условиях рыночной экономики, главным показателем рентабельности предприятия является прибыль. Поэтому очень важно понять, как необходимо вести хозяйство, что бы как говориться «не вылететь в трубу». И здесь незаменимы методы математической статистики, которые позволяют правильно оценить, какие факторы, и в какой степени влияют на прибыль, а так же на основании правильно построенной математической модели, спрогнозировать прибыль на будущий период.
1 ПОСТАНОВКА ЗАДАЧИ
Цель курсового проекта - сформировать профессиональные умения и навыки применения методов математической статистики к практическому анализу реальных физических процессов.
Цель задания – произвести статистический анализ исходных данных, полученных при исследовании основных показателей деятельности предприятия, с целью выявления доминирующих факторов влияющих на прибыль и построения адекватной математической модели для изучения возможностей ее максимизации и прогнозирования на последующие периоды.
Исходные данные для поставленного задания приведены в
таблице 1.1
Таблица 1.1 – Исходные данные для регрессионного анализа.
|
Прибыль |
Коэффициент качества продукции |
Доля в общем объеме продаж |
Розничная цена |
Коэффициент издержек на 1 продукции |
Удовлетворение условий розничных торговцев |
|
| № |
Y, % |
X1 |
X2 |
X3 |
X4 |
X5 |
|
1 |
1,99 |
1,22 |
1,24 |
1,3 |
35,19 |
2,08 |
|
2 |
12,21 |
1,45 |
1,54 |
1,04 |
80 |
1,09 |
|
3 |
23,07 |
1,9 |
1,31 |
1 |
23,31 |
2,28 |
|
4 |
24,14 |
2,53 |
1,36 |
1,64 |
80 |
1,44 |
|
5 |
35,05 |
3,41 |
2,65 |
1,19 |
80 |
1,75 |
|
6 |
36,87 |
1,96 |
1,63 |
1,26 |
68,84 |
1,54 |
|
7 |
4,7 |
2,71 |
1,66 |
1,28 |
80 |
0,47 |
|
8 |
58,45 |
1,76 |
1,4 |
1,42 |
30,32 |
2,51 |
|
9 |
59,55 |
2,09 |
2,61 |
1,65 |
80 |
2,81 |
|
10 |
61,42 |
1,1 |
2,42 |
1,24 |
32,94 |
0,59 |
|
11 |
61,51 |
3,62 |
3,5 |
1,09 |
28,56 |
0,64 |
|
12 |
61,95 |
3,53 |
1,29 |
1,29 |
78,75 |
1,73 |
|
13 |
71,24 |
2,09 |
2,44 |
1,65 |
38,63 |
1,83 |
|
14 |
71,45 |
1,54 |
2,6 |
1,19 |
48,67 |
0,76 |
Продолжение таблицы 1.1
|
15 |
81,88 |
2,41 |
2,11 |
1,64 |
40,83 |
0,14 |
|
16 |
10,08 |
3,64 |
2,06 |
1,46 |
80 |
3,53 |
|
17 |
10,25 |
2,61 |
1,85 |
1,59 |
80 |
2,13 |
|
18 |
10,81 |
2,62 |
2,28 |
1,57 |
80 |
3,86 |
|
19 |
11,09 |
3,29 |
4,07 |
1,78 |
80 |
1,28 |
|
20 |
12,64 |
1,24 |
1,84 |
1,38 |
31,2 |
4,25 |
|
21 |
12,92 |
1,37 |
1,9 |
1,55 |
29,49 |
3,98 |
Основная цель первой части задания оценить влияние на прибыль предприятия от реализации продукции одного вида следующих факторов:
Х1 - коэффициент качества продукции;
Х2 - доля в общем объеме продаж;
Х3 – розничная цена продукции;
Х4 – коэффициент издержек на единицу продукции;
Х5 – удовлетворение условий розничных торговцев.
Необходимо, применив регрессионные методы анализа, построить математическую модель зависимости прибыли от некоторых (или всех ) из вышеперечисленных факторов и проверить адекватность полученной модели.
2 Предварительный анализ исходных данных
Прежде чем применить к имеющимся у нас исходным данным метод регрессионного анализа, необходимо провести некоторый предварительный анализ имеющихся в нашем распоряжении выборок. Это позволит сделать выводы о качестве имеющихся в нашем распоряжении данных, а именно: о наличии или отсутствии тренда, нормальном законе распределения выборки, оценить некоторые статистические характеристики и т.д.
Для всех последующих расчетов примем уровень значимости 0.05, что соответствует 5% вероятности ошибки.
2.1 Исследование выборки по прибыли (Y).
Математическое ожидание (арифметическое среднее)
34,91761905.
Доверительный интервал для математического
ожидания (22,75083;47,08441).
Дисперсия (рассеивание) 714,402159.
Доверительный интервал для дисперсии (439,0531; 1564,384).
Средне квадратичное отклонение (от среднего) 26,72830258.
Медиана выборки 24,14.
Размах выборки 79,89.
Асимметрия (смещение от нормального распределения) 0,370221636.
Эксцесс выборки (отклонение от нормального распределения)
-1,551701276.
Коэффициент вариации (коэффициент представительности среднего) 77%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 2.1 (2-й столбец). Сумма серий равняется 5. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 2.1 (3-й столбец). Сумма инверсий равняется 81. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 2.1 – Критерии серий и инверсий.
|
Прибыль Y % |
Критерий серий |
Критерий инверсий |
|
1,99 |
- |
0 |
|
12,21 |
- |
5 |
|
23,07 |
- |
7 |
|
24,14 |
+ |
7 |
|
35,05 |
+ |
7 |
|
36,87 |
+ |
7 |
|
4,7 |
- |
0 |
|
58,45 |
+ |
6 |
|
59,55 |
+ |
6 |
|
61,42 |
+ |
6 |
|
61,51 |
+ |
6 |
|
61,95 |
+ |
6 |
|
71,24 |
+ |
6 |
|
71,45 |
+ |
6 |
|
81,88 |
+ |
6 |
|
10,08 |
- |
0 |
Продолжение таблицы 2.1
|
10,25 |
- |
0 |
|
10,81 |
- |
0 |
|
11,09 |
- |
0 |
|
12,64 |
- |
0 |
|
12,92 |
- |
0 |
|
Итого |
5 |
81 |
Проверка гипотезы о нормальном законе распределения выборки с применением критерия
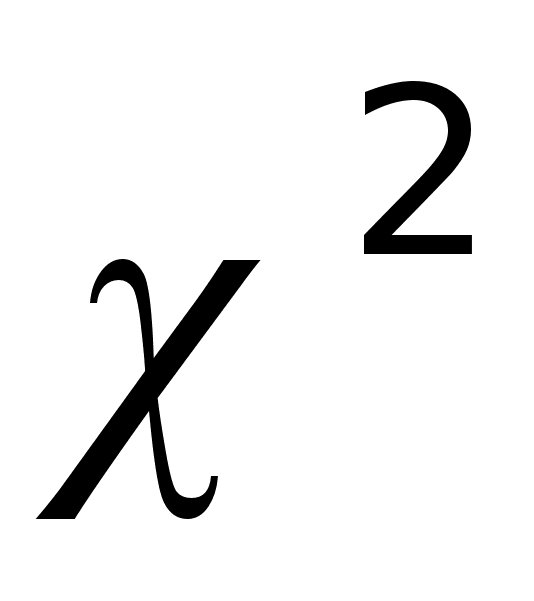 .
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
10,69132103.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=7.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в таблице 2.2.
.
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
10,69132103.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=7.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в таблице 2.2.
Таблица
2.2 – Критерий
![]() .
.
|
Интервалы группировки |
Теоретическая частота |
Расчетная частота |
|
12,68132103 |
0,221751084 |
4 |
|
23,37264207 |
0,285525351 |
2 |
|
34,0639631 |
0,313282748 |
1 |
|
44,75528414 |
0,2929147 |
2 |
|
55,44660517 |
0,233377369 |
0 |
|
66,1379262 |
0,158448887 |
5 |
|
76,82924724 |
0,091671119 |
2 |
Результирующее значение критерия 2,11526E-55 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
Исследование выборки по коэффициенту качества продукции (Х1).
Математическое ожидание (арифметическое среднее) 2,29.
Доверительный интервал для математического ожидания (1,905859236; 2,674140764).
Дисперсия (рассеивание) 0,71215.
Доверительный интервал для дисперсии (0,437669008; 1,559452555).
Средне квадратичное отклонение (от среднего) 0,843889803.
Медиана выборки 2,09.
Размах выборки 2,54.
Асимметрия (смещение от нормального распределения) 0,290734565.
Эксцесс выборки (отклонение от нормального распределения)
-1,161500717.
Коэффициент вариации (коэффициент представительности среднего) 37%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 2.3 (2-й столбец). Сумма серий равняется 11. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 2.3 (3-й столбец). Сумма инверсий равняется 89. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 2.3 – Критерии серий и инверсий.
|
Коэффициент качества продукции Х1 |
Критерий серий |
Критерий инверсий |
|
1,22 |
- |
1 |
|
1,45 |
- |
3 |
|
1,9 |
- |
5 |
|
2,53 |
+ |
9 |
|
3,41 |
+ |
13 |
|
1,96 |
- |
5 |
|
2,71 |
+ |
10 |
|
1,76 |
- |
4 |
|
2,09 |
+ |
4 |
|
1,1 |
- |
0 |
|
3,62 |
+ |
9 |
|
3,53 |
+ |
8 |
|
2,09 |
+ |
3 |
|
1,54 |
- |
2 |
|
2,41 |
+ |
2 |
|
3,64 |
+ |
5 |
|
2,61 |
+ |
2 |
|
2,62 |
+ |
2 |
|
3,29 |
+ |
2 |
|
1,24 |
- |
0 |
|
1,37 |
- |
0 |
|
Итого |
11 |
89 |
Проверка гипотезы о нормальном законе распределения выборки с применением критерия
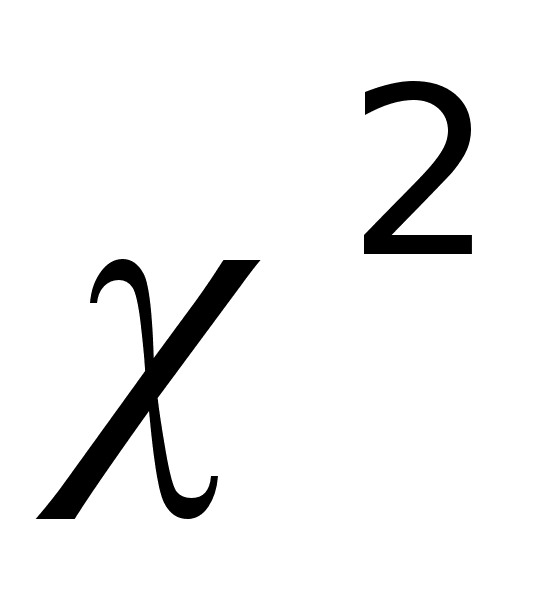 .
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
0,337555921.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=7.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в таблице 2.4.
.
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
0,337555921.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=7.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в таблице 2.4.
Таблица
2.4 – Критерий
![]() .
.
|
Интервалы группировки |
Теоретическая частота |
Расчетная частота |
|
1,437555921 |
5,960349765 |
4 |
|
1,775111843 |
8,241512255 |
3 |
|
2,112667764 |
9,71079877 |
4 |
|
2,450223685 |
9,750252967 |
1 |
|
2,787779606 |
8,342374753 |
4 |
|
3,125335528 |
6,082419779 |
0 |
|
3,462891449 |
3,778991954 |
2 |
Результирующее значение критерия 0,000980756 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
2.3 Исследование выборки по доле в общем объеме продаж (Х2).
Математическое ожидание (арифметическое среднее) 2,083809524.
Доверительный интервал для математического ожидания (1,748443949; 2,419175098).
Дисперсия (рассеивание) 0,542784762.
Доверительный интервал для дисперсии (0,333581504; 1,188579771).
Средне квадратичное отклонение (от среднего) 0,736739277.
Медиана выборки 1,9.
Размах выборки 2,83.
Асимметрия (смещение от нормального распределения) 1,189037981.
Эксцесс выборки (отклонение от нормального распределения)
1,48713312.
Коэффициент вариации (коэффициент представительности среднего) 35%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 2.5 (2-й столбец). Сумма серий равняется 11. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 2.5 (3-й столбец). Сумма инверсий равняется 89. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 2.5 – Критерии серий и инверсий.
|
Коэффициент качества продукции Х2 |
Критерий серий |
Критерий инверсий |
|
1,24 |
- |
0 |
|
1,54 |
- |
4 |
|
1,31 |
- |
1 |
|
1,36 |
- |
1 |
|
2,65 |
+ |
14 |
Продолжение таблицы 2.5
|
1,63 |
- |
2 |
|
1,66 |
- |
2 |
|
1,4 |
- |
1 |
|
2,61 |
+ |
10 |
|
2,42 |
+ |
7 |
|
3,5 |
+ |
9 |
|
1,29 |
- |
9 |
|
2,44 |
+ |
6 |
|
2,6 |
+ |
6 |
|
2,11 |
+ |
4 |
|
2,06 |
+ |
3 |
|
1,85 |
- |
1 |
|
2,28 |
+ |
2 |
|
4,07 |
+ |
2 |
|
1,84 |
- |
0 |
|
1,9 |
+ |
0 |
|
Итого |
10 |
84 |
Проверка гипотезы о нормальном законе распределения выборки с применением критерия
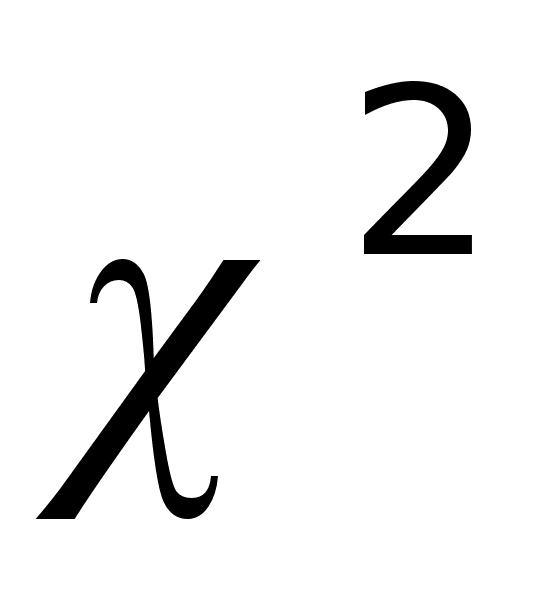 .
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
0,294695711.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=9.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в таблице 2.6.
.
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
0,294695711.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=9.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в таблице 2.6.
Таблица
2.6 – Критерий
![]() .
.
|
Интервалы группировки |
Теоретическая частота |
Расчетная частота |
|
1,534695711 |
8,613638207 |
5 |
|
1,829391421 |
10,71322271 |
3 |
|
2,124087132 |
11,35446101 |
5 |
|
2,418782843 |
10,25476697 |
1 |
|
2,713478553 |
7,892197623 |
5 |
|
3,008174264 |
5,175865594 |
0 |
|
3,302869975 |
2,892550245 |
0 |
|
3,597565686 |
1,377500344 |
1 |
|
3,892261396 |
0,559004628 |
1 |
Результирующее значение критерия 0,000201468 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
2.4 Исследование выборки по розничной цене (Х3).
Математическое ожидание (арифметическое среднее) 1,390952381.
Доверительный интервал для математического ожидания (1,287631388; 1,494273374).
Дисперсия (рассеивание) 0,051519048.
Доверительный интервал для дисперсии (0,031662277; 0,112815433).
Средне квадратичное отклонение (от среднего) 0,226978077.
Медиана выборки 1,38.
Размах выборки 0,78.
Асимметрия (смещение от нормального распределения) -0,060264426.
Эксцесс выборки (отклонение от нормального распределения)
-1,116579819.
Коэффициент вариации (коэффициент представительности среднего) 16%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 2.7 (2-й столбец). Сумма серий равняется 8. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 2.7 (3-й столбец). Сумма инверсий равняется 68. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 2.7 – Критерии серий и инверсий.
|
Розничная цена Х4 |
Критерий серий |
Критерий инверсий |
|
1,3 |
- |
9 |
|
1,04 |
- |
1 |
|
1 |
- |
0 |
|
1,64 |
+ |
13 |
|
1,19 |
- |
1 |
Продолжение таблицы 2.7
|
1,26 |
- |
3 |
|
1,28 |
- |
3 |
|
1,42 |
+ |
5 |
|
1,65 |
+ |
10 |
|
1,24 |
- |
2 |
|
1,09 |
- |
0 |
|
1,29 |
- |
1 |
|
1,65 |
+ |
7 |
|
1,19 |
- |
0 |
|
1,64 |
+ |
5 |
|
1,46 |
+ |
1 |
|
1,59 |
+ |
3 |
|
1,57 |
+ |
2 |
|
1,78 |
+ |
2 |
|
1,38 |
+ |
0 |
|
1,55 |
+ |
0 |
|
Итого |
8 |
68 |
Проверка гипотезы о нормальном законе распределения выборки с применением критерия
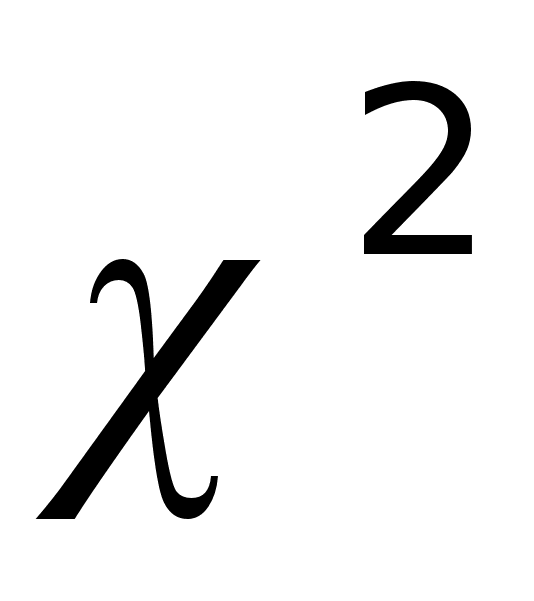 .
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
0,090791231.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=8.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в таблице 2.8.
.
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
0,090791231.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=8.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в таблице 2.8.
Таблица
2.8 – Критерий
![]() .
.
|
Интервалы группировки |
Теоретическая частота |
Расчетная частота |
|
1,090791231 |
15,39563075 |
3 |
|
1,181582462 |
24,12028441 |
0 |
|
1,272373693 |
32,20180718 |
4 |
|
1,363164924 |
36,63455739 |
3 |
|
1,453956155 |
35,51522214 |
2 |
|
1,544747386 |
29,33938492 |
1 |
|
1,635538617 |
20,65381855 |
3 |
|
1,726329848 |
12,38975141 |
4 |
Результирующее значение критерия 3,27644E-33 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
2.5 Исследование выборки по коэффициенту издержек на единицу продукции (Х4).
Математическое ожидание (арифметическое среднее) 57,46333333.
Доверительный интервал для математического ожидания (46,70536237; 68,22130429).
Дисперсия (рассеивание) 558,5363233.
Доверительный интервал для дисперсии (343,2620073; 1223,072241).
Средне квадратичное отклонение (от среднего) 23,63337308.
Медиана выборки 68,84.
Размах выборки 56,69.
Асимметрия (смещение от нормального распределения) --0,199328538.
Эксцесс выборки (отклонение от нормального распределения)
-1,982514776.
Коэффициент вариации (коэффициент представительности среднего) 41%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 2.9 (2-й столбец). Сумма серий равняется 11. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 2.9 (3-й столбец). Сумма инверсий равняется 89. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 2.9 – Критерии серий и инверсий
|
Розничная цена Х4 |
Критерий серий |
Критерий инверсий |
|
35,19 |
- |
6 |
|
80 |
+ |
11 |
|
23,31 |
- |
0 |
|
80 |
+ |
10 |
Продолжение таблицы 2.9.
|
80 |
+ |
10 |
|
68,84 |
+ |
8 |
|
80 |
+ |
9 |
|
30,32 |
- |
3 |
|
80 |
+ |
8 |
|
32,94 |
- |
3 |
|
28,56 |
- |
0 |
|
78,75 |
+ |
5 |
|
38,63 |
- |
2 |
|
48,67 |
- |
3 |
|
40,83 |
- |
2 |
|
80 |
+ |
2 |
|
80 |
+ |
2 |
|
80 |
+ |
2 |
|
80 |
+ |
2 |
|
31,2 |
- |
1 |
|
29,49 |
- |
0 |
|
Итого |
11 |
89 |
Проверка гипотезы о нормальном законе распределения выборки с применением критерия
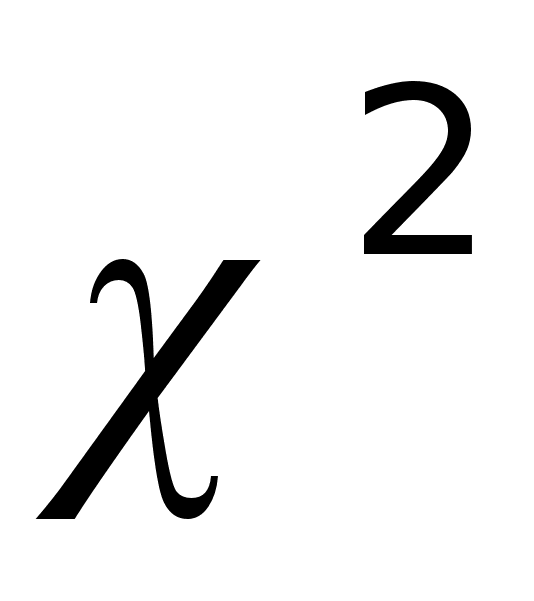 .
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
9,453349234.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=5.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в таблице 2.10.
.
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
9,453349234.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=5.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в таблице 2.10.
Таблица
2.10 – Критерий
![]() .
.
|
Интервалы группировки |
Теоретическая частота |
Расчетная частота |
|
32,76334923 |
0,205311711 |
5 |
|
42,21669847 |
0,287891016 |
4 |
|
51,6700477 |
0,343997578 |
1 |
|
61,12339693 |
0,350264029 |
0 |
|
70,57674617 |
0,30391251 |
1 |
Результирующее значение критерия 3,27644E-33 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
2.6 Исследование выборки по коэффициенту удовлетворения условий розничных торговцев (Х5).
Математическое ожидание (арифметическое среднее) 1,937619048.
Доверительный интервал для математического ожидания (1,390131506; 2,485106589).
Дисперсия (рассеивание) 1,446569048.
Доверительный интервал для дисперсии (0,889023998; 3,167669447).
Средне квадратичное отклонение (от среднего) 1,202733989.
Медиана выборки 1,75.
Размах выборки 4,11.
Асимметрия (смещение от нормального распределения) --0,527141402.
Эксцесс выборки (отклонение от нормального распределения)
-0,580795634.
Коэффициент вариации (коэффициент представительности среднего) 62%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 2.11 (2-й столбец). Сумма серий равняется 13. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 2.11 (3-й столбец). Сумма инверсий равняется 80. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 2.11 – Критерии серий и инверсий.
|
Розничная цена Х4 |
Критерий серий |
Критерий инверсий |
|
2,08 |
+ |
12 |
|
1,09 |
- |
5 |
|
2,28 |
+ |
12 |
|
1,44 |
- |
6 |
|
1,75 |
+ |
8 |
|
1,54 |
- |
6 |
Продолжение таблицы 2.11
|
0,47 |
- |
1 |
|
2,51 |
+ |
8 |
|
2,81 |
+ |
8 |
|
0,59 |
- |
1 |
|
0,64 |
- |
1 |
|
1,73 |
- |
3 |
|
1,83 |
+ |
3 |
|
0,76 |
- |
1 |
|
0,14 |
- |
0 |
|
3,53 |
+ |
2 |
|
2,13 |
+ |
1 |
|
3,86 |
+ |
1 |
|
1,28 |
- |
0 |
|
4,25 |
+ |
1 |
|
3,98 |
+ |
0 |
|
Итого |
13 |
80 |
Проверка гипотезы о нормальном законе распределения выборки с применением критерия
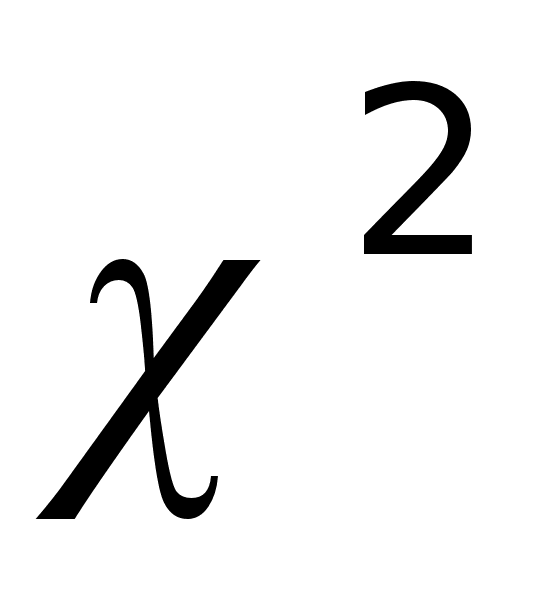 .
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
0,481093595.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=8.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в таблице 2.12.
.
Разобьем выборку
на интервалы
группировки
длиной 0,4*среднеквадратичное
отклонение
=
0,481093595.
Получим следующее
количество
интервалов
группировки
размах/длина
интервала=8.Все
данные о границах
интервалов,
теоретических
и эмпирических
частотах приведены
в таблице 2.12.
Таблица
2.12 – Критерий
![]() .
.
|
Интервалы группировки |
Теоретическая частота |
Расчетная частота |
|
0,621093595 |
3,826307965 |
3 |
|
1,102187191 |
5,47254967 |
3 |
|
1,583280786 |
6,669793454 |
3 |
|
2,064374382 |
6,927043919 |
3 |
|
2,545467977 |
6,130506823 |
4 |
|
3,026561573 |
4,623359901 |
1 |
|
3,507655168 |
2,971200139 |
0 |
|
3,988748764 |
1,627117793 |
3 |
Результирующее значение критерия 0,066231679 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
Построение математической модели
Корреляционный анализ.
Для оценки степени зависимости между переменными модели построим корреляционную матрицу, и для каждого коэффициента корреляции в матрице рассчитаем V-функцию, которая служит для проверки гипотезы об отсутствии корреляции между переменными.
Таблица 3.1. – Корреляционная матрица
|
Y |
X1 |
X2 |
X3 |
X4 |
X5 |
||
|
Y |
R |
0,95238 |
0,00950 |
0,21252 |
-0,01090 |
-0,30012 |
-0,42102 |
|
V |
8,30380 |
0,04247 |
0,96511 |
-0,04873 |
-1,38479 |
-2,00769 |
|
|
X1 |
R |
0,00950 |
0,95238 |
0,36487 |
0,13969 |
0,50352 |
-0,12555 |
|
V |
0,04247 |
8,30380 |
1,71054 |
0,62883 |
2,47761 |
-0,56445 |
|
|
X2 |
R |
0,21252 |
0,36487 |
0,95238 |
0,23645 |
0,06095 |
-0,19187 |
|
V |
0,96511 |
1,71054 |
8,30380 |
1,07781 |
0,27291 |
-0,86885 |
|
|
X3 |
R |
-0,01090 |
0,13969 |
0,23645 |
0,95238 |
0,24228 |
0,25014 |
|
V |
-0,04873 |
0,62883 |
1,07781 |
8,30380 |
1,10549 |
1,14293 |
|
|
X4 |
R |
-0,30012 |
0,50352 |
0,06095 |
0,24228 |
0,95238 |
-0,03955 |
|
V |
-1,38479 |
2,47761 |
0,27291 |
1,10549 |
8,30380 |
-0,17694 |
|
|
X5 |
R |
-0,42102 |
-0,12555 |
-0,19187 |
0,25014 |
-0,03955 |
0,95238 |
|
V |
-2,00769 |
-0,56445 |
-0,86885 |
1,14293 |
-0,17694 |
8,30380 |
Гипотеза
о нулевой корреляции
принимается
при –1,96
Регрессионный анализ.
Для построения математической модели выдвинем гипотезу о наличии линейной зависимости между прибылью (иначе Y) и факторами на нее влияющими (Х1, Х2, Х3, Х4, Х5). Следовательно, математическая модель может быть описана уравнением вида:
![]() , (3.1)
, (3.1)
где
![]() - линейно-независимые
постоянные
коэффициенты.
- линейно-независимые
постоянные
коэффициенты.
Для их отыскания применим множественный регрессионный анализ. Результаты регрессии сведены в таблицы 3.2 – 3.4.
Таблица 3.2.-Регрессионная статистика.
|
Множественный R |
0,609479083 |
|
R-квадрат |
0,371464753 |
|
Нормированный R-квадрат |
0,161953004 |
|
Стандартная ошибка |
24,46839969 |
|
Наблюдения |
21 |
Таблица 3.3. –Дисперсионная таблица.
|
|
Степени свободы |
SS |
MS |
F |
Значимость F |
|
Регрессия |
5 |
5307,504428 |
1061,500886 |
1,773002013 |
0,179049934 |
|
Остаток |
15 |
8980,538753 |
598,7025835 |
||
|
Итого |
20 |
14288,04318 |
Таблица 3.4 – Коэффициенты регрессии.
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|
|
B0 |
38,950215 |
35,7610264 |
1,0891805 |
0,29326 |
-37,272 |
115,173 |
-37,2726 |
115,173 |
|
B1 |
4,5371110 |
8,42440677 |
0,5385674 |
0,59808 |
-13,419 |
22,4933 |
-13,4190 |
22,4933 |
|
B2 |
1,8305781 |
8,73999438 |
0,2094484 |
0,83691 |
-16,798 |
20,4594 |
-16,7982 |
20,4594 |
|
B3 |
23,645979 |
27,4788285 |
0,8605162 |
0,40304 |
-34,923 |
82,2157 |
-34,9237 |
82,2157 |
|
B4 |
-0,526248 |
0,28793074 |
-1,827690 |
0,08755 |
-1,1399 |
0,08746 |
-1,13995 |
0,08746 |
|
B5 |
-10,780037 |
4,95649626 |
-2,174931 |
0,04604 |
-21,344 |
-0,21550 |
-21,3445 |
-0,21550 |
Таким образом, уравнение, описывающее математическую модель, приобретает вид:
Y=4,53711108952303*X1+1,830578196*X2+23,64597929*X3- 0,526248308*X5-10,78003746*X5+38,95021506. (3.2)
Для
оценки влияния
каждого из
факторов на
результирующую
математическую
модель применим
метод множественной
линейной регрессии
к нормированным
значениям
переменных
![]() ,
результаты
пересчета
коэффициентов
приведены в
таблице 3.5.
,
результаты
пересчета
коэффициентов
приведены в
таблице 3.5.
Таблица 3.5. – Оценка влияния факторов.
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
|
|
Y-пересечение |
38,95021506 |
35,76102644 |
1,089180567 |
|
Переменная X 1 |
3,828821785 |
7,109270974 |
0,538567428 |
|
Переменная X 2 |
1,348658856 |
6,439097143 |
0,209448441 |
|
Переменная X 3 |
5,367118917 |
6,237091662 |
0,86051628 |
|
Переменная X 4 |
-12,43702261 |
6,804774783 |
-1,827690556 |
|
Переменная X 5 |
-12,96551745 |
5,961346518 |
-2,174931018 |
Коэффициенты в таблице 3.5 показывают степень влияния каждой из переменных на результат (Y). Чем больше коэффициент, тем сильнее прямая зависимость (отрицательные коэффициенты показывают обратную зависимость).
F-критерий из таблицы 3.3 показывает степень адекватности полученной математической модели.
ВЫВОДЫ
В результате проведенной работы был произведен статистический анализ исходных данных, полученных при исследовании основных показателей деятельности предприятия, с целью выявления доминирующих факторов влияющих на прибыль и построена адекватная математическая модель и спрогнозирована прибыль на последующие периоды.
В процессе выполнения работы изучили и научились применять на практике следующие методы математической статистики:
линейный регрессионный анализ,
множественный регрессионный анализ,
корреляционный анализ,
проверка стационарности и независимости выборок,
выявление тренда,
критерий
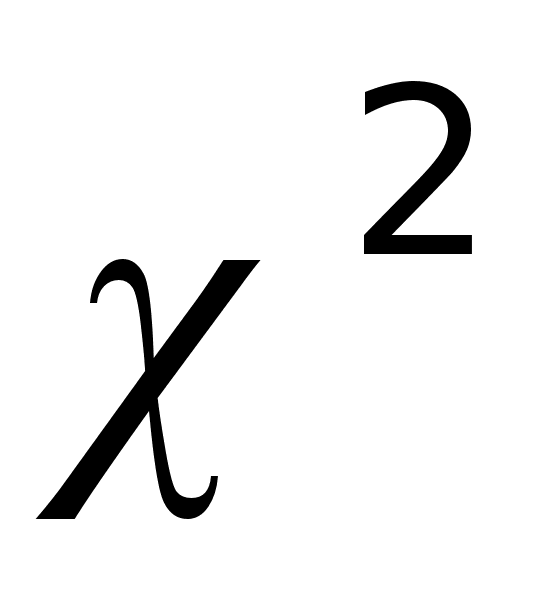 .
.
Перечень ссылок
Бендод Дж., Пирсол А. Прикладной анализ случайных данных: Пер. с англ. – М.: Мир, 1989.
Математическая статистика. Под ред. А. М. Длина, М.: Высшая школа, 1975.
Л.Н.Большев, Н.В.Смирнов. Таблицы математической статистики.-М.: Наука, 1983.
Н.Дрейпер, Г.Смит. Прикладной регрессионный анализ. Пер. с англ.- М.: Статистика, 1973.
Overview
Временные ряды_ИДРегрессионный анализ_ИД
Регрессия
Анализ У
Анализ Х1
Анализ Х2
Анализ Х3
Анализ Х4
Анализ Х5
Sheet 1: Временные ряды_ИД
| Месяц | 1994 | 1996 | 1997 | 1998 |
| Январь | 1500000 | 1650000 | 1400000 | 1700000 |
| Февраль | 900000 | 850000 | 890000 | 1200000 |
| Март | 700000 | 600000 | 550000 | 459000 |
| Апрель | 300000 | 125000 | 250000 | 221000 |
| Май | 400000 | 300000 | 100000 | 1000 |
| Июнь | 250000 | 450000 | 150000 | 250000 |
| Июль | 200000 | 600000 | 132000 | 325000 |
| Август | 150000 | 750000 | 142000 | 354000 |
| Сентябрь | 300000 | 300000 | 254000 | 150000 |
| Октябрь | 250000 | 259000 | 350000 | 100000 |
| Ноябрь | 400000 | 453000 | 450000 | 259000 |
| Декабрь | 2000000 | 1700000 | 1000000 | 1900000 |
Sheet 2: Регрессионный анализ_ИД
| Прибыль | Коэффициент качества продукции | Доля в общем объеме продаж | Розничная цена | Коэффициент издержек на 1 продукции | Удовлетворение условий розничных торговцев | Отклонение от среднего | Отклонение от среднего | Отклонение от среднего | Отклонение от среднего | Отклонение от среднего | Отклонение от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | |||
| № | Y, % | X1 | X2 | X3 | X4 | X5 | Y | X1 | X2 | X3 | X4 | X5 | Y | X1 | X2 | X3 | X4 | X5 | ||
| 1 | 1.99 | 1.22 | 1.24 | 1.3 | 35.19 | 2.08 | -32.93 | -1.07 | -0.84 | -0.09 | -22.27 | 0.14 | 1084.23 | 1.14 | 0.71 | 0.01 | 496.1 | 0.02 | ||
| 2 | 12.21 | 1.45 | 1.54 | 1.04 | 80 | 1.09 | -22.71 | -0.84 | -0.54 | -0.35 | 22.54 | -0.85 | 515.64 | 0.71 | 0.3 | 0.12 | 507.9 | 0.72 | ||
| 3 | 23.07 | 1.9 | 1.31 | 1 | 23.31 | 2.28 | -11.85 | -0.39 | -0.77 | -0.39 | -34.15 | 0.34 | 140.37 | 0.15 | 0.6 | 0.15 | 1166.45 | 0.12 | ||
| 4 | 24.14 | 2.53 | 1.36 | 1.64 | 80 | 1.44 | -10.78 | 0.24 | -0.72 | 0.25 | 22.54 | -0.5 | 116.16 | 0.06 | 0.52 | 0.06 | 507.9 | 0.25 | ||
| 5 | 35.05 | 3.41 | 2.65 | 1.19 | 80 | 1.75 | 0.13 | 1.12 | 0.57 | -0.2 | 22.54 | -0.19 | 0.02 | 1.25 | 0.32 | 0.04 | 507.9 | 0.04 | ||
| 6 | 36.87 | 1.96 | 1.63 | 1.26 | 68.84 | 1.54 | 1.95 | -0.33 | -0.45 | -0.13 | 11.38 | -0.4 | 3.81 | 0.11 | 0.21 | 0.02 | 129.43 | 0.16 | ||
| 7 | 4.7 | 2.71 | 1.66 | 1.28 | 80 | 0.47 | -30.22 | 0.42 | -0.42 | -0.11 | 22.54 | -1.47 | 913.1 | 0.18 | 0.18 | 0.01 | 507.9 | 2.15 | ||
| 8 | 58.45 | 1.76 | 1.4 | 1.42 | 30.32 | 2.51 | 23.53 | -0.53 | -0.68 | 0.03 | -27.14 | 0.57 | 553.77 | 0.28 | 0.47 | 0 | 736.76 | 0.33 | ||
| 9 | 59.55 | 2.09 | 2.61 | 1.65 | 80 | 2.81 | 24.63 | -0.2 | 0.53 | 0.26 | 22.54 | 0.87 | 606.75 | 0.04 | 0.28 | 0.07 | 507.9 | 0.76 | ||
| 10 | 61.42 | 1.1 | 2.42 | 1.24 | 32.94 | 0.59 | 26.5 | -1.19 | 0.34 | -0.15 | -24.52 | -1.35 | 702.38 | 1.42 | 0.11 | 0.02 | 601.39 | 1.82 | ||
| 11 | 61.51 | 3.62 | 3.5 | 1.09 | 28.56 | 0.64 | 26.59 | 1.33 | 1.42 | -0.3 | -28.9 | -1.3 | 707.15 | 1.77 | 2.01 | 0.09 | 835.4 | 1.68 | ||
| 12 | 61.95 | 3.53 | 1.29 | 1.29 | 78.75 | 1.73 | 27.03 | 1.24 | -0.79 | -0.1 | 21.29 | -0.21 | 730.75 | 1.54 | 0.63 | 0.01 | 453.12 | 0.04 | ||
| 13 | 71.24 | 2.09 | 2.44 | 1.65 | 38.63 | 1.83 | 36.32 | -0.2 | 0.36 | 0.26 | -18.83 | -0.11 | 1319.32 | 0.04 | 0.13 | 0.07 | 354.69 | 0.01 | ||
| 14 | 71.45 | 1.54 | 2.6 | 1.19 | 48.67 | 0.76 | 36.53 | -0.75 | 0.52 | -0.2 | -8.79 | -1.18 | 1334.61 | 0.56 | 0.27 | 0.04 | 77.32 | 1.39 | ||
| 15 | 81.88 | 2.41 | 2.11 | 1.64 | 40.83 | 0.14 | 46.96 | 0.12 | 0.03 | 0.25 | -16.63 | -1.8 | 2205.47 | 0.01 | 0 | 0.06 | 276.67 | 3.23 | ||
| 16 | 10.08 | 3.64 | 2.06 | 1.46 | 80 | 3.53 | -24.84 | 1.35 | -0.02 | 0.07 | 22.54 | 1.59 | 616.91 | 1.82 | 0 | 0 | 507.9 | 2.54 | ||
| 17 | 10.25 | 2.61 | 1.85 | 1.59 | 80 | 2.13 | -24.67 | 0.32 | -0.23 | 0.2 | 22.54 | 0.19 | 608.49 | 0.1 | 0.05 | 0.04 | 507.9 | 0.04 | ||
| 18 | 10.81 | 2.62 | 2.28 | 1.57 | 80 | 3.86 | -24.11 | 0.33 | 0.2 | 0.18 | 22.54 | 1.92 | 581.18 | 0.11 | 0.04 | 0.03 | 507.9 | 3.7 | ||
| 19 | 11.09 | 3.29 | 4.07 | 1.78 | 80 | 1.28 | -23.83 | 1 | 1.99 | 0.39 | 22.54 | -0.66 | 567.76 | 1 | 3.94 | 0.15 | 507.9 | 0.43 | ||
| 20 | 12.64 | 1.24 | 1.84 | 1.38 | 31.2 | 4.25 | -22.28 | -1.05 | -0.24 | -0.01 | -26.26 | 2.31 | 496.29 | 1.1 | 0.06 | 0 | 689.76 | 5.35 | ||
| 21 | 12.92 | 1.37 | 1.9 | 1.55 | 29.49 | 3.98 | -22 | -0.92 | -0.18 | 0.16 | -27.97 | 2.04 | 483.9 | 0.85 | 0.03 | 0.03 | 782.51 | 4.17 | ||
| Среднее по столбцу | Среднее по столбцу | Среднее по столбцу | Среднее по столбцу | Среднее по столбцу | Среднее по столбцу | Погрешность | Погрешность | Погрешность | Погрешность | Погрешность | Погрешность | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | |||
| M(X) | 34.92 | 2.29 | 2.08 | 1.39 | 57.46 | 1.94 | 0 | 0 | 0 | 0 | 0 | 0 | 714.4 | 0.71 | 0.54 | 0.05 | 558.54 | 1.45 | ||
| Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | |||||||||||||||
| D(X) | 714.4 | 0.71 | 0.54 | 0.05 | 558.54 | 1.45 | ||||||||||||||
| S2 | 26.73 | 0.84 | 0.74 | 0.23 | 23.63 | 1.2 | ||||||||||||||
| Ковариционная матрица | ||||||||||||||||||||
| Y | X1 | X2 | X3 | X4 | X5 | |||||||||||||||
| Y | 680.38 | 0.21 | 4.18 | -0.07 | -189.58 | -13.53 | ||||||||||||||
| X1 | 0.21 | 0.68 | 0.23 | 0.03 | 10.04 | -0.13 | ||||||||||||||
| X2 | 4.18 | 0.23 | 0.52 | 0.04 | 1.06 | -0.17 | ||||||||||||||
| X3 | -0.07 | 0.03 | 0.04 | 0.05 | 1.3 | 0.07 | ||||||||||||||
| X4 | -189.58 | 10.04 | 1.06 | 1.3 | 531.94 | -1.12 | ||||||||||||||
| X5 | -13.53 | -0.13 | -0.17 | 0.07 | -1.12 | 1.38 | ||||||||||||||
| Кореляционная матрица | ||||||||||||||||||||
| Y | X1 | X2 | X3 | X4 | X5 | |||||||||||||||
| Y | R | 0.95 | 0.01 | 0.21 | -0.01 | -0.3 | -0.42 | |||||||||||||
| V | 8.3 | 0.04 | 0.97 | -0.05 | -1.38 | -2.01 | ||||||||||||||
| X1 | R | 0.01 | 0.95 | 0.36 | 0.14 | 0.5 | -0.13 | |||||||||||||
| V | 0.04 | 8.3 | 1.71 | 0.63 | 2.48 | -0.56 | ||||||||||||||
| X2 | R | 0.21 | 0.36 | 0.95 | 0.24 | 0.06 | -0.19 | |||||||||||||
| V | 0.97 | 1.71 | 8.3 | 1.08 | 0.27 | -0.87 | ||||||||||||||
| X3 | R | -0.01 | 0.14 | 0.24 | 0.95 | 0.24 | 0.25 | |||||||||||||
| V | -0.05 | 0.63 | 1.08 | 8.3 | 1.11 | 1.14 | ||||||||||||||
| X4 | R | -0.3 | 0.5 | 0.06 | 0.24 | 0.95 | -0.04 | |||||||||||||
| V | -1.38 | 2.48 | 0.27 | 1.11 | 8.3 | -0.18 | ||||||||||||||
| X5 | R | -0.42 | -0.13 | -0.19 | 0.25 | -0.04 | 0.95 | |||||||||||||
| V | -2.01 | -0.56 | -0.87 | 1.14 | -0.18 | 8.3 | ||||||||||||||
| Область принятия гипотезы | -1.96 | 1.96 | ||||||||||||||||||
Sheet 3: Регрессия
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0.01 | |||||||
| R-квадрат | 0 | |||||||
| Нормированный R-квадрат | -0.05 | |||||||
| Стандартная ошибка | 27.42 | |||||||
| Наблюдения | 21 | |||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 1 | 1.42 | 1.42 | 0 | 0.97 | |||
| Остаток | 19 | 14286.62 | 751.93 | |||||
| Итого | 20 | 14288.04 | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 34.19 | 17.68 | 1.93 | 0.07 | -2.81 | 71.2 | -2.81 | 71.2 |
| Переменная X 1 | 0.32 | 7.27 | 0.04 | 0.97 | -14.89 | 15.52 | -14.89 | 15.52 |
| ВЫВОД ОСТАТКА | ||||||||
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки | |||||
| 1 | 34.58 | -32.59 | -1.28 | |||||
| 2 | 34.65 | -22.44 | -0.88 | |||||
| 3 | 34.79 | -11.72 | -0.46 | |||||
| 4 | 34.99 | -10.85 | -0.43 | |||||
| 6 | 34.81 | 2.06 | 0.08 | |||||
| 7 | 35.05 | -30.35 | -1.19 | |||||
| 8 | 34.75 | 23.7 | 0.93 | |||||
| 9 | 34.85 | 24.7 | 0.97 | |||||
| 10 | 34.54 | 26.88 | 1.06 | |||||
| 11 | 35.34 | 26.17 | 1.03 | |||||
| 12 | 35.31 | 26.64 | 1.05 | |||||
| 14 | 34.68 | 36.77 | 1.44 | |||||
| 15 | 34.96 | 46.92 | 1.84 | |||||
| 16 | 35.34 | -25.26 | -0.99 | |||||
| 17 | 35.02 | -24.77 | -0.97 | |||||
| 18 | 35.02 | -24.21 | -0.95 | |||||
| 19 | 35.23 | -24.14 | -0.95 | |||||
| 20 | 34.59 | -21.95 | -0.86 | |||||
| 21 | 34.63 | -21.71 | -0.85 | |||||
Sheet 4: Анализ У
| Прибыль | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| Y, % | 7 | ||||
| 1.99 | - | 0 | 8 | 12.68 | 0.22 |
| 12.21 | - | 0 | 2 | 23.37 | 0.29 |
| 23.07 | - | 0 | 1 | 34.06 | 0.31 |
| 24.14 | + | 0 | 2 | 44.76 | 0.29 |
| 35.05 | + | 0 | 0 | 55.45 | 0.23 |
| 36.87 | + | 0 | 5 | 66.14 | 0.16 |
| 4.7 | - | 0 | 2 | 76.83 | 0.09 |
| 58.45 | + | 0 | |||
| 59.55 | + | 0 | |||
| 61.42 | + | 0 | |||
| 61.51 | + | 0 | |||
| 61.95 | + | 0 | |||
| 71.24 | + | 0 | |||
| 71.45 | + | 0 | |||
| 81.88 | + | 0 | |||
| 10.08 | - | 0 | |||
| 10.25 | - | 0 | |||
| 10.81 | - | 0 | |||
| 11.09 | - | 0 | |||
| 12.64 | - | 0 | |||
| 12.92 | - | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 34.92 | 22.75 | 47.08 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 714.4 | 439.05 | 1564.38 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 26.73 | Критерий серий | Err:502 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 24.14 | 5 | 5 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12.6 | |||
| 79.89 | |||||
| Вариация | Критерий инверсий | ||||
| 77% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 0 | 125 | ||
| 0.37 | тренд отсутствует | ||||
| Эксцес | |||||
| -1.55 | |||||
Sheet 5: Анализ Х1
| Коэффициент качества продукции | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X1 | 7 | ||||
| 1.22 | - | 0 | 4 | 1.44 | 5.96 |
| 1.45 | - | 0 | 3 | 1.78 | 8.24 |
| 1.9 | - | 0 | 4 | 2.11 | 9.71 |
| 2.53 | + | 0 | 1 | 2.45 | 9.75 |
| 3.41 | + | 0 | 4 | 2.79 | 8.34 |
| 1.96 | - | 0 | 0 | 3.13 | 6.08 |
| 2.71 | + | 0 | 2 | 3.46 | 3.78 |
| 1.76 | - | 0 | |||
| 2.09 | + | 0 | |||
| 1.1 | - | 0 | |||
| 3.62 | + | 0 | |||
| 3.53 | + | 0 | |||
| 2.09 | + | 0 | |||
| 1.54 | - | 0 | |||
| 2.41 | + | 0 | |||
| 3.64 | + | 0 | |||
| 2.61 | + | 0 | |||
| 2.62 | + | 0 | |||
| 3.29 | + | 0 | |||
| 1.24 | - | 0 | |||
| 1.37 | - | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 2.29 | 1.91 | 2.67 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 0.71 | 0.44 | 1.56 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 0.84 | Критерий серий | Err:502 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 2.09 | 5 | 11 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12.6 | |||
| 2.54 | |||||
| Вариация | Критерий инверсий | ||||
| 37% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 0 | 125 | ||
| 0.29 | тренд отсутствует | ||||
| Эксцес | |||||
| -1.16 | |||||
Sheet 6: Анализ Х2
| Доля в общем объеме продаж | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X2 | 9 | ||||
| 1.24 | - | 0 | 5 | 1.53 | 8.61 |
| 1.54 | - | 0 | 3 | 1.83 | 10.71 |
| 1.31 | - | 0 | 5 | 2.12 | 11.35 |
| 1.36 | - | 0 | 1 | 2.42 | 10.25 |
| 2.65 | + | 0 | 5 | 2.71 | 7.89 |
| 1.63 | - | 0 | 0 | 3.01 | 5.18 |
| 1.66 | - | 0 | 0 | 3.3 | 2.89 |
| 1.4 | - | 0 | 1 | 3.6 | 1.38 |
| 2.61 | + | 0 | 1 | 3.89 | 0.56 |
| 2.42 | + | 0 | |||
| 3.5 | + | 0 | |||
| 1.29 | - | 9 | |||
| 2.44 | + | 0 | |||
| 2.6 | + | 0 | |||
| 2.11 | + | 0 | |||
| 2.06 | + | 0 | |||
| 1.85 | - | 0 | |||
| 2.28 | + | 0 | |||
| 4.07 | + | 0 | |||
| 1.84 | - | 0 | |||
| 1.9 | + | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 2.08 | 1.75 | 2.42 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 0.54 | 0.33 | 1.19 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 0.74 | Критерий серий | 0 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 1.9 | 5 | 10 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12.6 | |||
| 2.83 | |||||
| Вариация | Критерий инверсий | ||||
| 35% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 9 | 125 | ||
| 1.19 | тренд отсутствует | ||||
| Эксцес | |||||
| 1.49 | |||||
Sheet 7: Анализ Х3
| Розничная цена | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X3 | 8 | ||||
| 1.3 | - | 0 | 3 | 1.09 | 15.4 |
| 1.04 | - | 0 | 0 | 1.18 | 24.12 |
| 1 | - | 0 | 4 | 1.27 | 32.2 |
| 1.64 | + | 0 | 3 | 1.36 | 36.63 |
| 1.19 | - | 0 | 2 | 1.45 | 35.52 |
| 1.26 | - | 0 | 1 | 1.54 | 29.34 |
| 1.28 | - | 0 | 3 | 1.64 | 20.65 |
| 1.42 | + | 0 | 4 | 1.73 | 12.39 |
| 1.65 | + | 0 | |||
| 1.24 | - | 0 | |||
| 1.09 | - | 0 | |||
| 1.29 | - | 0 | |||
| 1.65 | + | 0 | |||
| 1.19 | - | 0 | |||
| 1.64 | + | 0 | |||
| 1.46 | + | 0 | |||
| 1.59 | + | 0 | |||
| 1.57 | + | 0 | |||
| 1.78 | + | 0 | |||
| 1.38 | + | 0 | |||
| 1.55 | + | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 1.39 | 1.29 | 1.49 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 0.05 | 0.03 | 0.11 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 0.23 | Критерий серий | 0 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 1.38 | 5 | 8 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12.6 | |||
| 0.78 | |||||
| Вариация | Критерий инверсий | ||||
| 16% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 0 | 125 | ||
| -0.06 | тренд отсутствует | ||||
| Эксцес | |||||
| -1.12 | |||||
Sheet 8: Анализ Х4
| Коэффициент издержек на 1 продукции | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X4 | 5 | ||||
| 35.19 | - | 0 | 5 | 32.76 | 0.21 |
| 80 | + | 11 | 4 | 42.22 | 0.29 |
| 23.31 | - | 0 | 1 | 51.67 | 0.34 |
| 80 | + | 10 | 0 | 61.12 | 0.35 |
| 80 | + | 10 | 1 | 70.58 | 0.3 |
| 68.84 | + | 0 | |||
| 80 | + | 9 | |||
| 30.32 | - | 0 | |||
| 80 | + | 8 | |||
| 32.94 | - | 0 | |||
| 28.56 | - | 0 | |||
| 78.75 | + | 0 | |||
| 38.63 | - | 0 | |||
| 48.67 | - | 0 | |||
| 40.83 | - | 0 | |||
| 80 | + | 2 | |||
| 80 | + | 2 | |||
| 80 | + | 2 | |||
| 80 | + | 2 | |||
| 31.2 | - | 0 | |||
| 29.49 | - | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 57.46 | 46.71 | 68.22 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 558.54 | 343.26 | 1223.07 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 23.63 | Критерий серий | Err:502 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 68.84 | 5 | 11 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12.6 | |||
| 56.69 | |||||
| Вариация | Критерий инверсий | ||||
| 41% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 56 | 125 | ||
| -0.2 | тренд отсутствует | ||||
| Эксцес | |||||
| -1.98 | |||||
Sheet 9: Анализ Х5
| Удовлетворение условий розничных торговцев | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X5 | 8 | ||||
| 2.08 | + | 0 | 3 | 0.62 | 3.83 |
| 1.09 | - | 0 | 3 | 1.1 | 5.47 |
| 2.28 | + | 0 | 3 | 1.58 | 6.67 |
| 1.44 | - | 0 | 3 | 2.06 | 6.93 |
| 1.75 | + | 0 | 4 | 2.55 | 6.13 |
| 1.54 | - | 0 | 1 | 3.03 | 4.62 |
| 0.47 | - | 0 | 0 | 3.51 | 2.97 |
| 2.51 | + | 0 | 3 | 3.99 | 1.63 |
| 2.81 | + | 0 | |||
| 0.59 | - | 0 | |||
| 0.64 | - | 0 | |||
| 1.73 | - | 0 | |||
| 1.83 | + | 0 | |||
| 0.76 | - | 0 | |||
| 0.14 | - | 0 | |||
| 3.53 | + | 0 | |||
| 2.13 | + | 0 | |||
| 3.86 | + | 0 | |||
| 1.28 | - | 0 | |||
| 4.25 | + | 0 | |||
| 3.98 | + | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 1.94 | 1.39 | 2.49 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 1.45 | 0.89 | 3.17 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 1.2 | Критерий серий | 0.07 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 1.75 | 5 | 13 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12.6 | |||
| 4.11 | |||||
| Вариация | Критерий инверсий | ||||
| 62% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 0 | 125 | ||
| 0.53 | тренд отсутствует | ||||
| Эксцес | |||||
| -0.58 | |||||
Overview
Временные ряды-РегрессияВременные ряды_ИД
Анализ У
Регрессионный анализ_ИД
Пошаговая регрессия
Множественная регрессия
Оценка влияния факторов
Влияние коэфициентов
Анализ Х1
Анализ Х2
Анализ Х3
Анализ Х4
Анализ Х5
Sheet 1: Временные ряды-Регрессия
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0.1 | |||||||
| R-квадрат | 0.01 | |||||||
| Нормированный R-квадрат | -0.01 | |||||||
| Стандартная ошибка | 537056.5 | |||||||
| Наблюдения | 48 | |||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 1 | 123884446808.51 | 123884446808.51 | 0.43 | 0.52 | |||
| Остаток | 46 | 13267765469858.2 | 288429684127.35 | |||||
| Итого | 47 | 13391649916666.7 | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 672637.41 | 157489.39 | 4.27 | 0 | 355628.02 | 989646.8 | 355628.02 | 989646.8 |
| Переменная X 1 | -3667.17 | 5595.55 | -0.66 | 0.52 | -14930.43 | 7596.08 | -14930.43 | 7596.08 |
| ВЫВОД ОСТАТКА | ||||||||
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки | |||||
| 1 | 668970.24 | 831029.76 | 1.56 | |||||
| 2 | 665303.06 | 234696.94 | 0.44 | |||||
| 3 | 661635.89 | 38364.11 | 0.07 | |||||
| 4 | 657968.72 | -357968.72 | -0.67 | |||||
| 5 | 654301.55 | -254301.55 | -0.48 | |||||
| 6 | 650634.37 | -400634.37 | -0.75 | |||||
| 7 | 646967.2 | -446967.2 | -0.84 | |||||
| 8 | 643300.03 | -493300.03 | -0.93 | |||||
| 9 | 639632.85 | -339632.85 | -0.64 | |||||
| 10 | 635965.68 | -385965.68 | -0.73 | |||||
| 11 | 632298.51 | -232298.51 | -0.44 | |||||
| 12 | 628631.33 | 1371368.67 | 2.58 | |||||
| 13 | 624964.16 | 1025035.84 | 1.93 | |||||
| 14 | 621296.99 | 228703.01 | 0.43 | |||||
| 15 | 617629.81 | -17629.81 | -0.03 | |||||
| 16 | 613962.64 | -488962.64 | -0.92 | |||||
| 17 | 610295.47 | -310295.47 | -0.58 | |||||
| 18 | 606628.29 | -156628.29 | -0.29 | |||||
| 19 | 602961.12 | -2961.12 | -0.01 | |||||
| 20 | 599293.95 | 150706.05 | 0.28 | |||||
| 21 | 595626.77 | -295626.77 | -0.56 | |||||
| 22 | 591959.6 | -332959.6 | -0.63 | |||||
| 23 | 588292.43 | -135292.43 | -0.25 | |||||
| 24 | 584625.25 | 1115374.75 | 2.1 | |||||
| 25 | 580958.08 | 819041.92 | 1.54 | |||||
| 26 | 577290.91 | 312709.09 | 0.59 | |||||
| 27 | 573623.73 | -23623.73 | -0.04 | |||||
| 28 | 569956.56 | -319956.56 | -0.6 | |||||
| 29 | 566289.39 | -466289.39 | -0.88 | |||||
| 30 | 562622.21 | -412622.21 | -0.78 | |||||
| 31 | 558955.04 | -426955.04 | -0.8 | |||||
| 32 | 555287.87 | -413287.87 | -0.78 | |||||
| 33 | 551620.69 | -297620.69 | -0.56 | |||||
| 34 | 547953.52 | -197953.52 | -0.37 | |||||
| 35 | 544286.35 | -94286.35 | -0.18 | |||||
| 36 | 540619.17 | 459380.83 | 0.86 | |||||
| 37 | 536952 | 1163048 | 2.19 | |||||
| 38 | 533284.83 | 666715.17 | 1.25 | |||||
| 39 | 529617.65 | -70617.65 | -0.13 | |||||
| 40 | 525950.48 | -304950.48 | -0.57 | |||||
| 41 | 522283.31 | -521283.31 | -0.98 | |||||
| 42 | 518616.13 | -268616.13 | -0.51 | |||||
| 43 | 514948.96 | -189948.96 | -0.36 | |||||
| 44 | 511281.79 | -157281.79 | -0.3 | |||||
| 45 | 507614.61 | -357614.61 | -0.67 | |||||
| 46 | 503947.44 | -403947.44 | -0.76 | |||||
| 47 | 500280.27 | -241280.27 | -0.45 | |||||
| 48 | 496613.1 | 1403386.9 | 2.64 | |||||
Sheet 2: Временные ряды_ИД
| Месяц | 1994 | 1996 | 1997 | 1998 | 0 | 0 | ||||||||||||||||
| Январь | 1500000 | 1650000 | 1400000 | 1700000 | 1 | 668970.24 | 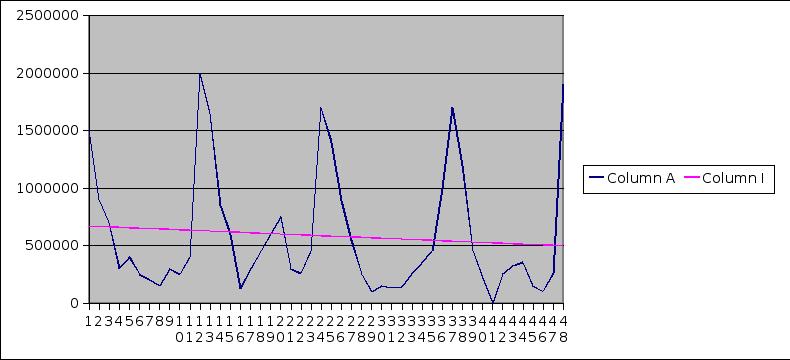
|
|||||||||||||||
| Февраль | 900000 | 850000 | 890000 | 1200000 | 2 | 665303.06 | 841271126736.11 | |||||||||||||||
| Март | 700000 | 600000 | 550000 | 459000 | 3 | 661635.89 | 100621126736.11 | |||||||||||||||
| Апрель | 300000 | 125000 | 250000 | 221000 | 4 | 657968.72 | 13737793402.78 | |||||||||||||||
| Май | 400000 | 300000 | 100000 | 1000 | 5 | 654301.55 | 79971126736.11 | |||||||||||||||
| Июнь | 250000 | 450000 | 150000 | 250000 | 6 | 650634.37 | 33412793402.78 | |||||||||||||||
| Июль | 200000 | 600000 | 132000 | 325000 | 7 | 646967.2 | 110750293402.78 | |||||||||||||||
| Август | 150000 | 750000 | 142000 | 354000 | 8 | 643300.03 | 146529460069.45 | |||||||||||||||
| Сентябрь | 300000 | 300000 | 254000 | 150000 | 9 | 639632.85 | 187308626736.11 | |||||||||||||||
| Октябрь | 250000 | 259000 | 350000 | 100000 | 10 | 635965.68 | 79971126736.11 | |||||||||||||||
| Ноябрь | 400000 | 453000 | 450000 | 259000 | 11 | 632298.51 | 110750293402.78 | |||||||||||||||
| Декабрь | 2000000 | 1700000 | 1000000 | 1900000 | 12 | 628631.33 | 33412793402.78 | |||||||||||||||
| 13 | 624964.16 | 2008479460069.44 | ||||||||||||||||||||
| 14 | 621296.99 | 1138933626736.11 | ||||||||||||||||||||
| 1994 | 1996 | 1997 | 1998 | 15 | 617629.81 | 71400293402.78 | ||||||||||||||||
| Январь | 224% | 264% | 241% | 317% | 16 | 613962.64 | 296126736.11 | |||||||||||||||
| Февраль | 135% | 137% | 154% | 225% | 17 | 610295.47 | 209573210069.45 | |||||||||||||||
| Март | 106% | 97% | 96% | 87% | 18 | 606628.29 | 79971126736.11 | |||||||||||||||
| Апрель | 46% | 20% | 44% | 42% | 19 | 602961.12 | 17633626736.11 | |||||||||||||||
| Май | 61% | 49% | 18% | 0% | 20 | 599293.95 | 296126736.11 | |||||||||||||||
| Июнь | 38% | 74% | 27% | 48% | 21 | 595626.77 | 27958626736.11 | |||||||||||||||
| Июль | 31% | 100% | 24% | 63% | 22 | 591959.6 | 79971126736.11 | |||||||||||||||
| Август | 23% | 125% | 26% | 69% | 23 | 588292.43 | 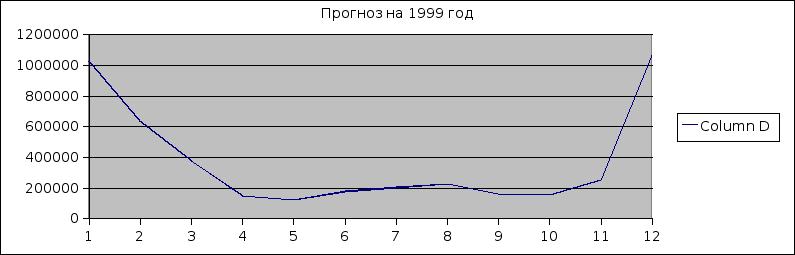
|
104841043402.78 | ||||||||||||||
| Сентябрь | 47% | 50% | 46% | 30% | 24 | 584625.25 | 16845876736.11 | |||||||||||||||
| Октябрь | 39% | 44% | 64% | 20% | 25 | 580958.08 | 1248154460069.44 | |||||||||||||||
| Ноябрь | 63% | 77% | 83% | 52% | 26 | 577290.91 | 667829460069.45 | |||||||||||||||
| Декабрь | 318% | 291% | 185% | 383% | 27 | 573623.73 | 94376960069.44 | |||||||||||||||
| 28 | 569956.56 | 1075293402.78 | ||||||||||||||||||||
| Сезонные индексы | Тренд | Прогноз на 1999 | 29 | 566289.39 | 110750293402.78 | |||||||||||||||||
| Январь | 209% | 492945.92 | 1031068.82 | 30 | 562622.21 | 233087793402.78 | ||||||||||||||||
| Февраль | 130% | 489278.75 | 637311.12 | 31 | 558955.04 | 187308626736.11 | ||||||||||||||||
| Март | 77% | 485611.58 | 374398.66 | 32 | 555287.87 | 203213126736.11 | ||||||||||||||||
| Апрель | 30% | 481944.4 | 146353.57 | 33 | 551620.69 | 194297293402.78 | ||||||||||||||||
| Май | 26% | 478277.23 | 122573.55 | 34 | 547953.52 | 108103960069.45 | ||||||||||||||||
| Июнь | 37% | 474610.06 | 177950.9 | 35 | 544286.35 | 54191960069.44 | ||||||||||||||||
| Июль | 43% | 470942.88 | 204531.36 | 36 | 540619.17 | 17633626736.11 | ||||||||||||||||
| Август | 49% | 467275.71 | 227352.63 | 37 | 536952 | 174062793402.78 | ||||||||||||||||
| Сентябрь | 35% | 463608.54 | 160283.5 | 38 | 533284.83 | 1248154460069.44 | ||||||||||||||||
| Октябрь | 33% | 459941.36 | 153418.64 | 39 | 529617.65 | 380946126736.11 | ||||||||||||||||
| Ноябрь | 55% | 456274.19 | 250687.84 | 40 | 525950.48 | 15324376736.11 | ||||||||||||||||
| Декабрь | 235% | 452607.02 | 1064984.99 | 41 | 522283.31 | 130893210069.45 | ||||||||||||||||
| 42 | 518616.13 | 338481543402.78 | ||||||||||||||||||||
| 43 | 514948.96 | 110750293402.78 | ||||||||||||||||||||
| Прибыль | Критерий серий | Критерий инверсий | Интервалы группировки | Расчетная чястота | Теоретическая частота | 44 | 511281.79 | 66456543402.78 | ||||||||||||||
| 1500000 | + | 42 | 9 | 45 | 507614.61 | 52345626736.11 | ||||||||||||||||
| 900000 | + | 1 | 212279.04 | 10 | 0 | 46 | 503947.44 | 187308626736.11 | ||||||||||||||
| 700000 | + | 34 | 423558.08 | 17 | 0 | 47 | 500280.27 | 233087793402.78 | ||||||||||||||
| 300000 | - | 18 | 634837.12 | 7 | 0 | 48 | 496613.1 | 104841043402.78 | ||||||||||||||
| 400000 | - | 24 | 846116.16 | 2 | 0 | 1735037793402.78 | ||||||||||||||||
| 250000 | - | 11 | 1057395.2 | 4 | 0 | Дисперсия по столбцу | ||||||||||||||||
| 200000 | - | 9 | 1268674.24 | 1 | 0 | 278992706597.22 | ||||||||||||||||
| 150000 | - | 6 | 1479953.29 | 1 | 0 | |||||||||||||||||
| 300000 | - | 15 | 1691232.33 | 2 | 0 | |||||||||||||||||
| 250000 | - | 9 | 1902511.37 | 3 | 0 | |||||||||||||||||
| 400000 | - | 19 | ||||||||||||||||||||
| 2000000 | + | 36 | ||||||||||||||||||||
| 1650000 | + | 32 | ||||||||||||||||||||
| 850000 | + | 27 | ||||||||||||||||||||
| 600000 | + | 24 | ||||||||||||||||||||
| 125000 | - | 3 | ||||||||||||||||||||
| 300000 | - | 13 | ||||||||||||||||||||
| 450000 | - | 17 | ||||||||||||||||||||
| 600000 | + | 21 | ||||||||||||||||||||
| 750000 | + | 21 | ||||||||||||||||||||
| 300000 | - | 13 | ||||||||||||||||||||
| 259000 | - | 11 | ||||||||||||||||||||
| 453000 | - | 16 | ||||||||||||||||||||
| 1700000 | + | 22 | ||||||||||||||||||||
| 1400000 | + | 21 | ||||||||||||||||||||
| 890000 | + | 18 | ||||||||||||||||||||
| 550000 | - | 17 | ||||||||||||||||||||
| 250000 | - | 8 | ||||||||||||||||||||
| 100000 | - | 1 | ||||||||||||||||||||
| 150000 | - | 4 | ||||||||||||||||||||
| 132000 | - | 2 | ||||||||||||||||||||
| 142000 | - | 2 | ||||||||||||||||||||
| 254000 | - | 5 | ||||||||||||||||||||
| 350000 | - | 7 | ||||||||||||||||||||
| 450000 | - | 8 | ||||||||||||||||||||
| 1000000 | + | 9 | ||||||||||||||||||||
| 1700000 | + | 10 | ||||||||||||||||||||
| 1200000 | + | 9 | ||||||||||||||||||||
| 459000 | - | 8 | ||||||||||||||||||||
| 221000 | - | 3 | ||||||||||||||||||||
| 1000 | - | 0 | ||||||||||||||||||||
| 250000 | - | 2 | ||||||||||||||||||||
| 325000 | - | 3 | ||||||||||||||||||||
| 354000 | - | 3 | ||||||||||||||||||||
| 150000 | - | 1 | ||||||||||||||||||||
| 100000 | - | 0 | ||||||||||||||||||||
| 259000 | - | 0 | ||||||||||||||||||||
| 1900000 | + | 0 | ||||||||||||||||||||
| Cреднее по столбцу | Доверительный интервал | |||||||||||||||||||||
| 582791.67 | 429399.29 | 736184.05 | ||||||||||||||||||||
| Дисперсия по столбцу | Доверительный интервал | |||||||||||||||||||||
| 278992706597.22 | 220975011966.12 | 536744052806.77 | ||||||||||||||||||||
| Cреднее квадратичное отклонение | ||||||||||||||||||||||
| 528197.6 | Критерий серий | |||||||||||||||||||||
| Медиана | 18 | 10 | 33 | Хи-квадрат критерий | ||||||||||||||||||
| 352000 | 0 | |||||||||||||||||||||
| Размах | Критерий инверсий | Табличное значение | ||||||||||||||||||||
| 1999000 | 495 | 585 | 729 | 55.76 | ||||||||||||||||||
| Вариация | ||||||||||||||||||||||
| 91% | ||||||||||||||||||||||
| Ассиметрия | ||||||||||||||||||||||
| 1.37 | ||||||||||||||||||||||
| Эксцес | ||||||||||||||||||||||
| 0.8 | ||||||||||||||||||||||
Sheet 3: Анализ У
| Прибыль | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| Y, % | 7 | ||||
| 1.99 | - | 0 | 8 | 12.68 | 0.22 |
| 12.21 | - | 0 | 2 | 23.37 | 0.29 |
| 23.07 | - | 0 | 1 | 34.06 | 0.31 |
| 24.14 | + | 0 | 2 | 44.76 | 0.29 |
| 35.05 | + | 0 | 0 | 55.45 | 0.23 |
| 36.87 | + | 0 | 5 | 66.14 | 0.16 |
| 4.7 | - | 0 | 2 | 76.83 | 0.09 |
| 58.45 | + | 0 | |||
| 59.55 | + | 0 | |||
| 61.42 | + | 0 | |||
| 61.51 | + | 0 | |||
| 61.95 | + | 0 | |||
| 71.24 | + | 0 | |||
| 71.45 | + | 0 | |||
| 81.88 | + | 0 | |||
| 10.08 | - | 0 | |||
| 10.25 | - | 0 | |||
| 10.81 | - | 0 | |||
| 11.09 | - | 0 | |||
| 12.64 | - | 0 | |||
| 12.92 | - | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 34.92 | 22.75 | 47.08 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 714.4 | 439.05 | 1564.38 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 26.73 | Критерий серий | Err:502 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 24.14 | 5 | 5 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12.6 | |||
| 79.89 | |||||
| Вариация | Критерий инверсий | ||||
| 77% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 0 | 125 | ||
| 0.37 | тренд отсутствует | ||||
| Эксцес | |||||
| -1.55 | |||||
Sheet 4: Регрессионный анализ_ИД
| Прибыль | Коэффициент качества продукции | Доля в общем объеме продаж | Розничная цена | Коэффициент издержек на 1 продукции | Удовлетворение условий розничных торговцев | Отклонение от среднего | Отклонение от среднего | Отклонение от среднего | Отклонение от среднего | Отклонение от среднего | Отклонение от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | |||
| № | Y, % | X1 | X2 | X3 | X4 | X5 | Y | X1 | X2 | X3 | X4 | X5 | Y | X1 | X2 | X3 | X4 | X5 | ||
| 1 | 1.99 | 1.22 | 1.24 | 1.3 | 35.19 | 2.08 | -32.93 | -1.07 | -0.84 | -0.09 | -22.27 | 0.14 | 1084.23 | 1.14 | 0.71 | 0.01 | 496.1 | 0.02 | ||
| 2 | 12.21 | 1.45 | 1.54 | 1.04 | 80 | 1.09 | -22.71 | -0.84 | -0.54 | -0.35 | 22.54 | -0.85 | 515.64 | 0.71 | 0.3 | 0.12 | 507.9 | 0.72 | ||
| 3 | 23.07 | 1.9 | 1.31 | 1 | 23.31 | 2.28 | -11.85 | -0.39 | -0.77 | -0.39 | -34.15 | 0.34 | 140.37 | 0.15 | 0.6 | 0.15 | 1166.45 | 0.12 | ||
| 4 | 24.14 | 2.53 | 1.36 | 1.64 | 80 | 1.44 | -10.78 | 0.24 | -0.72 | 0.25 | 22.54 | -0.5 | 116.16 | 0.06 | 0.52 | 0.06 | 507.9 | 0.25 | ||
| 5 | 35.05 | 3.41 | 2.65 | 1.19 | 80 | 1.75 | 0.13 | 1.12 | 0.57 | -0.2 | 22.54 | -0.19 | 0.02 | 1.25 | 0.32 | 0.04 | 507.9 | 0.04 | ||
| 6 | 36.87 | 1.96 | 1.63 | 1.26 | 68.84 | 1.54 | 1.95 | -0.33 | -0.45 | -0.13 | 11.38 | -0.4 | 3.81 | 0.11 | 0.21 | 0.02 | 129.43 | 0.16 | ||
| 7 | 4.7 | 2.71 | 1.66 | 1.28 | 80 | 0.47 | -30.22 | 0.42 | -0.42 | -0.11 | 22.54 | -1.47 | 913.1 | 0.18 | 0.18 | 0.01 | 507.9 | 2.15 | ||
| 8 | 58.45 | 1.76 | 1.4 | 1.42 | 30.32 | 2.51 | 23.53 | -0.53 | -0.68 | 0.03 | -27.14 | 0.57 | 553.77 | 0.28 | 0.47 | 0 | 736.76 | 0.33 | ||
| 9 | 59.55 | 2.09 | 2.61 | 1.65 | 80 | 2.81 | 24.63 | -0.2 | 0.53 | 0.26 | 22.54 | 0.87 | 606.75 | 0.04 | 0.28 | 0.07 | 507.9 | 0.76 | ||
| 10 | 61.42 | 1.1 | 2.42 | 1.24 | 32.94 | 0.59 | 26.5 | -1.19 | 0.34 | -0.15 | -24.52 | -1.35 | 702.38 | 1.42 | 0.11 | 0.02 | 601.39 | 1.82 | ||
| 11 | 61.51 | 3.62 | 3.5 | 1.09 | 28.56 | 0.64 | 26.59 | 1.33 | 1.42 | -0.3 | -28.9 | -1.3 | 707.15 | 1.77 | 2.01 | 0.09 | 835.4 | 1.68 | ||
| 12 | 61.95 | 3.53 | 1.29 | 1.29 | 78.75 | 1.73 | 27.03 | 1.24 | -0.79 | -0.1 | 21.29 | -0.21 | 730.75 | 1.54 | 0.63 | 0.01 | 453.12 | 0.04 | ||
| 13 | 71.24 | 2.09 | 2.44 | 1.65 | 38.63 | 1.83 | 36.32 | -0.2 | 0.36 | 0.26 | -18.83 | -0.11 | 1319.32 | 0.04 | 0.13 | 0.07 | 354.69 | 0.01 | ||
| 14 | 71.45 | 1.54 | 2.6 | 1.19 | 48.67 | 0.76 | 36.53 | -0.75 | 0.52 | -0.2 | -8.79 | -1.18 | 1334.61 | 0.56 | 0.27 | 0.04 | 77.32 | 1.39 | ||
| 15 | 81.88 | 2.41 | 2.11 | 1.64 | 40.83 | 0.14 | 46.96 | 0.12 | 0.03 | 0.25 | -16.63 | -1.8 | 2205.47 | 0.01 | 0 | 0.06 | 276.67 | 3.23 | ||
| 16 | 10.08 | 3.64 | 2.06 | 1.46 | 80 | 3.53 | -24.84 | 1.35 | -0.02 | 0.07 | 22.54 | 1.59 | 616.91 | 1.82 | 0 | 0 | 507.9 | 2.54 | ||
| 17 | 10.25 | 2.61 | 1.85 | 1.59 | 80 | 2.13 | -24.67 | 0.32 | -0.23 | 0.2 | 22.54 | 0.19 | 608.49 | 0.1 | 0.05 | 0.04 | 507.9 | 0.04 | ||
| 18 | 10.81 | 2.62 | 2.28 | 1.57 | 80 | 3.86 | -24.11 | 0.33 | 0.2 | 0.18 | 22.54 | 1.92 | 581.18 | 0.11 | 0.04 | 0.03 | 507.9 | 3.7 | ||
| 19 | 11.09 | 3.29 | 4.07 | 1.78 | 80 | 1.28 | -23.83 | 1 | 1.99 | 0.39 | 22.54 | -0.66 | 567.76 | 1 | 3.94 | 0.15 | 507.9 | 0.43 | ||
| 20 | 12.64 | 1.24 | 1.84 | 1.38 | 31.2 | 4.25 | -22.28 | -1.05 | -0.24 | -0.01 | -26.26 | 2.31 | 496.29 | 1.1 | 0.06 | 0 | 689.76 | 5.35 | ||
| 21 | 12.92 | 1.37 | 1.9 | 1.55 | 29.49 | 3.98 | -22 | -0.92 | -0.18 | 0.16 | -27.97 | 2.04 | 483.9 | 0.85 | 0.03 | 0.03 | 782.51 | 4.17 | ||
| Среднее по столбцу | Среднее по столбцу | Среднее по столбцу | Среднее по столбцу | Среднее по столбцу | Среднее по столбцу | Погрешность | Погрешность | Погрешность | Погрешность | Погрешность | Погрешность | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | |||
| M(X) | 34.92 | 2.29 | 2.08 | 1.39 | 57.46 | 1.94 | 0 | 0 | 0 | 0 | 0 | 0 | 714.4 | 0.71 | 0.54 | 0.05 | 558.54 | 1.45 | ||
| Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | |||||||||||||||
| D(X) | 714.4 | 0.71 | 0.54 | 0.05 | 558.54 | 1.45 | ||||||||||||||
| S2 | 26.73 | 0.84 | 0.74 | 0.23 | 23.63 | 1.2 | ||||||||||||||
| Ковариционная матрица | ||||||||||||||||||||
| Y | X1 | X2 | X3 | X4 | X5 | |||||||||||||||
| Y | 680.38 | 0.21 | 4.18 | -0.07 | -189.58 | -13.53 | ||||||||||||||
| X1 | 0.21 | 0.68 | 0.23 | 0.03 | 10.04 | -0.13 | ||||||||||||||
| X2 | 4.18 | 0.23 | 0.52 | 0.04 | 1.06 | -0.17 | ||||||||||||||
| X3 | -0.07 | 0.03 | 0.04 | 0.05 | 1.3 | 0.07 | ||||||||||||||
| X4 | -189.58 | 10.04 | 1.06 | 1.3 | 531.94 | -1.12 | ||||||||||||||
| X5 | -13.53 | -0.13 | -0.17 | 0.07 | -1.12 | 1.38 | ||||||||||||||
| Кореляционная матрица | ||||||||||||||||||||
| Y | X1 | X2 | X3 | X4 | X5 | |||||||||||||||
| Y | R | 0.95 | 0.01 | 0.21 | -0.01 | -0.3 | -0.42 | |||||||||||||
| V | 8.3 | 0.04 | 0.97 | -0.05 | -1.38 | -2.01 | ||||||||||||||
| X1 | R | 0.01 | 0.95 | 0.36 | 0.14 | 0.5 | -0.13 | |||||||||||||
| V | 0.04 | 8.3 | 1.71 | 0.63 | 2.48 | -0.56 | ||||||||||||||
| X2 | R | 0.21 | 0.36 | 0.95 | 0.24 | 0.06 | -0.19 | |||||||||||||
| V | 0.97 | 1.71 | 8.3 | 1.08 | 0.27 | -0.87 | ||||||||||||||
| X3 | R | -0.01 | 0.14 | 0.24 | 0.95 | 0.24 | 0.25 | |||||||||||||
| V | -0.05 | 0.63 | 1.08 | 8.3 | 1.11 | 1.14 | ||||||||||||||
| X4 | R | -0.3 | 0.5 | 0.06 | 0.24 | 0.95 | -0.04 | |||||||||||||
| V | -1.38 | 2.48 | 0.27 | 1.11 | 8.3 | -0.18 | ||||||||||||||
| X5 | R | -0.42 | -0.13 | -0.19 | 0.25 | -0.04 | 0.95 | |||||||||||||
| V | -2.01 | -0.56 | -0.87 | 1.14 | -0.18 | 8.3 | ||||||||||||||
| Область принятия гипотезы | -1.96 | 1.96 | ||||||||||||||||||
Sheet 5: Пошаговая регрессия
| Шаг 0 | Альфа | 0.05 | F-включения, мин | 4.00 | F-удаления, мин | 4.49 | ||
| X1 | X2 | X3 | X4 | X5 | ||||
| r | 0.01 | 0.21 | -0.01 | -0.3 | -0.42 | |||
| F | 0 | 0.9 | 0 | 1.88 | 4.09 | |||
| Шаг 1 | ||||||||
| Включаем X5 | ||||||||
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0.44 | |||||||
| R-квадрат | 0.2 | |||||||
| Нормированный R-квадрат | 0.15 | |||||||
| Стандартная ошибка | 24.6 | |||||||
| Наблюдения | 21 | |||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 1 | 2792.29 | 2792.29 | 4.62 | 0.04 | |||
| Остаток | 19 | 11495.75 | 605.04 | |||||
| Итого | 20 | 14288.04 | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 53.95 | 10.36 | 5.21 | 0 | 32.27 | 75.64 | 32.27 | 75.64 |
| Переменная X 1 | -9.82 | 4.57 | -2.15 | 0.04 | -19.4 | -0.25 | -19.4 | -0.25 |
| X1 | X2 | X3 | X4 | X5 | ||||
| r | -0.39 | -0.05 | -0.93 | -0.87 | ||||
| F | 3.18 | 0.04 | 119.46 | 58.62 | ||||
| Шаг 2 | ||||||||
| Включаем X3 | ||||||||
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0.55 | |||||||
| R-квадрат | 0.31 | |||||||
| Нормированный R-квадрат | 0.23 | |||||||
| Стандартная ошибка | 23.46 | |||||||
| Наблюдения | 21 | |||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 2 | 4383.99 | 2191.99 | 3.98 | 0.04 | |||
| Остаток | 18 | 9904.06 | 550.23 | |||||
| Итого | 20 | 14288.04 | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 76.26 | 16.42 | 4.64 | 0 | 41.76 | 110.76 | 41.76 | 110.76 |
| Переменная X 1 | -0.38 | 0.22 | -1.7 | 0.11 | -0.84 | 0.09 | -0.84 | 0.09 |
| Переменная X 2 | -10.13 | 4.36 | -2.32 | 0.03 | -19.3 | -0.96 | -19.3 | -0.96 |
| X5 | X3 | |||||||
| F-удаления | 7.97 | 7.97 | ||||||
| X1 | X2 | X4 | ||||||
| r | -0.84 | -0.61 | -1.62 | |||||
| F | 39.15 | 10.2 | -27.42 | |||||
| Шаг3 | ||||||||
| Включаем X1 | ||||||||
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0.46 | |||||||
| R-квадрат | 0.21 | |||||||
| Нормированный R-квадрат | 0.07 | |||||||
| Стандартная ошибка | 25.73 | |||||||
| Наблюдения | 21 | |||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 3 | 3031.59 | 1010.53 | 1.53 | 0.24 | |||
| Остаток | 17 | 11256.45 | 662.14 | |||||
| Итого | 20 | 14288.04 | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 40.33 | 37.28 | 1.08 | 0.29 | -38.33 | 118.99 | -38.33 | 118.99 |
| Переменная X 1 | -2.3 | 7.01 | -0.33 | 0.75 | -17.08 | 12.48 | -17.08 | 12.48 |
| Переменная X 2 | 14.9 | 26.76 | 0.56 | 0.58 | -41.55 | 71.36 | -41.55 | 71.36 |
| Переменная X 3 | -10.78 | 5.04 | -2.14 | 0.05 | -21.41 | -0.14 | -21.41 | -0.14 |
| X1 | X3 | X5 | ||||||
| F-удаления | 4.58 | 4.58 | 4.58 | |||||
| X2 | X4 | |||||||
| r | -0.74 | -0.98 | ||||||
| F | 19.2 | 508 | ||||||
| ШАГ4 | ||||||||
| Включаем X4 | ||||||||
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0.61 | |||||||
| R-квадрат | 0.37 | |||||||
| Нормированный R-квадрат | 0.21 | |||||||
| Стандартная ошибка | 23.73 | |||||||
| Наблюдения | 21 | |||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 4 | 5281.24 | 1320.31 | 2.35 | 0.1 | |||
| Остаток | 16 | 9006.8 | 562.93 | |||||
| Итого | 20 | 14288.04 | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 39.93 | 34.38 | 1.16 | 0.26 | -32.94 | 112.81 | -32.94 | 112.81 |
| Переменная X 1 | 5.25 | 7.48 | 0.7 | 0.49 | -10.61 | 21.1 | -10.61 | 21.1 |
| Переменная X 2 | 25.49 | 25.23 | 1.01 | 0.33 | -28 | 78.99 | -28 | 78.99 |
| Переменная X 3 | -0.54 | 0.27 | -2 | 0.06 | -1.11 | 0.03 | -1.11 | 0.03 |
| Переменная X 4 | -11.04 | 4.65 | -2.38 | 0.03 | -20.9 | -1.19 | -20.9 | -1.19 |
| X1 | X3 | X4 | X5 | |||||
| F-удаления | 9.38 | 9.38 | 9.38 | 9.38 | ||||
| X2 | ||||||||
| r | -1.75 | |||||||
| F | 72.79 | |||||||
| ШАГ5 | ||||||||
| Включаем X2 | ||||||||
Sheet 6: Множественная регрессия
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0.61 | |||||||
| R-квадрат | 0.37 | |||||||
| Нормированный R-квадрат | 0.16 | |||||||
| Стандартная ошибка | 24.47 | |||||||
| Наблюдения | 21 | |||||||
| Дисперсионный анализ | ||||||||
| Степени свободы | SS | MS | F | Значимость F | ||||
| Регрессия | 5 | 5307.5 | 1061.5 | 1.77 | 0.18 | |||
| Остаток | 15 | 8980.54 | 598.7 | |||||
| Итого | 20 | 14288.04 | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 38.95 | 35.76 | 1.09 | 0.29 | -37.27 | 115.17 | -37.27 | 115.17 |
| Переменная X 1 | 4.54 | 8.42 | 0.54 | 0.6 | -13.42 | 22.49 | -13.42 | 22.49 |
| Переменная X 2 | 1.83 | 8.74 | 0.21 | 0.84 | -16.8 | 20.46 | -16.8 | 20.46 |
| Переменная X 3 | 23.65 | 27.48 | 0.86 | 0.4 | -34.92 | 82.22 | -34.92 | 82.22 |
| Переменная X 4 | -0.53 | 0.29 | -1.83 | 0.09 | -1.14 | 0.09 | -1.14 | 0.09 |
| Переменная X 5 | -10.78 | 4.96 | -2.17 | 0.05 | -21.34 | -0.22 | -21.34 | -0.22 |
| ВЫВОД ОСТАТКА | ||||||||
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки | |||||
| 2 | 19.09 | -6.88 | -0.39 | |||||
| 3 | 36.77 | -13.7 | -0.78 | |||||
| 4 | 34.07 | -9.93 | -0.56 | |||||
| 5 | 26.45 | 8.6 | 0.49 | |||||
| 6 | 27.79 | 9.08 | 0.52 | |||||
| 7 | 37.38 | -32.68 | -1.86 | |||||
| 8 | 40.06 | 18.39 | 1.04 | |||||
| 10 | 54 | 7.42 | 0.42 | |||||
| 11 | 65.63 | -4.12 | -0.23 | |||||
| 12 | 27.74 | 34.21 | 1.94 | |||||
| 13 | 51.86 | 19.38 | 1.1 | |||||
| 14 | 45.03 | 26.42 | 1.5 | |||||
| 15 | 69.53 | 12.35 | 0.7 | |||||
| 16 | 13.61 | -3.53 | -0.2 | |||||
| 17 | 26.71 | -16.46 | -0.93 | |||||
| 18 | 8.42 | 2.39 | 0.14 | |||||
| 19 | 47.52 | -36.43 | -2.07 | |||||
| 20 | 18.34 | -5.7 | -0.32 | |||||
| 21 | 26.87 | -13.95 | -0.79 | |||||
| Результат регрессии | Y=4,53711108952303*X1+1,830578196*X2+23,64597929*X3-0,526248308*X5-10,78003746*X5+38,95021506 | |||||||
Sheet 7: Оценка влияния факторов
| Прибыль | Коэффициент качества продукции | Доля в общем объеме продаж | Розничная цена | Коэффициент издержек на 1 продукции | Удовлетворение условий розничных торговцев | ||||||
| № | Y, % | X1 | X2 | X3 | X4 | X5 | Z1 | Z2 | Z3 | Z4 | Z5 |
| 1 | 1.99 | 1.22 | 1.24 | 1.3 | 35.19 | 2.08 | 1.45 | 1.68 | 5.73 | 1.49 | 1.73 |
| 2 | 12.21 | 1.45 | 1.54 | 1.04 | 80 | 1.09 | 1.72 | 2.09 | 4.58 | 3.39 | 0.91 |
| 3 | 23.07 | 1.9 | 1.31 | 1 | 23.31 | 2.28 | 2.25 | 1.78 | 4.41 | 0.99 | 1.9 |
| 4 | 24.14 | 2.53 | 1.36 | 1.64 | 80 | 1.44 | 3 | 1.85 | 7.23 | 3.39 | 1.2 |
| 5 | 35.05 | 3.41 | 2.65 | 1.19 | 80 | 1.75 | 4.04 | 3.6 | 5.24 | 3.39 | 1.46 |
| 6 | 36.87 | 1.96 | 1.63 | 1.26 | 68.84 | 1.54 | 2.32 | 2.21 | 5.55 | 2.91 | 1.28 |
| 7 | 4.7 | 2.71 | 1.66 | 1.28 | 80 | 0.47 | 3.21 | 2.25 | 5.64 | 3.39 | 0.39 |
| 8 | 58.45 | 1.76 | 1.4 | 1.42 | 30.32 | 2.51 | 2.09 | 1.9 | 6.26 | 1.28 | 2.09 |
| 9 | 59.55 | 2.09 | 2.61 | 1.65 | 80 | 2.81 | 2.48 | 3.54 | 7.27 | 3.39 | 2.34 |
| 10 | 61.42 | 1.1 | 2.42 | 1.24 | 32.94 | 0.59 | 1.3 | 3.28 | 5.46 | 1.39 | 0.49 |
| 11 | 61.51 | 3.62 | 3.5 | 1.09 | 28.56 | 0.64 | 4.29 | 4.75 | 4.8 | 1.21 | 0.53 |
| 12 | 61.95 | 3.53 | 1.29 | 1.29 | 78.75 | 1.73 | 4.18 | 1.75 | 5.68 | 3.33 | 1.44 |
| 13 | 71.24 | 2.09 | 2.44 | 1.65 | 38.63 | 1.83 | 2.48 | 3.31 | 7.27 | 1.63 | 1.52 |
| 14 | 71.45 | 1.54 | 2.6 | 1.19 | 48.67 | 0.76 | 1.82 | 3.53 | 5.24 | 2.06 | 0.63 |
| 15 | 81.88 | 2.41 | 2.11 | 1.64 | 40.83 | 0.14 | 2.86 | 2.86 | 7.23 | 1.73 | 0.12 |
| 16 | 10.08 | 3.64 | 2.06 | 1.46 | 80 | 3.53 | 4.31 | 2.8 | 6.43 | 3.39 | 2.93 |
| 17 | 10.25 | 2.61 | 1.85 | 1.59 | 80 | 2.13 | 3.09 | 2.51 | 7.01 | 3.39 | 1.77 |
| 18 | 10.81 | 2.62 | 2.28 | 1.57 | 80 | 3.86 | 3.1 | 3.09 | 6.92 | 3.39 | 3.21 |
| 19 | 11.09 | 3.29 | 4.07 | 1.78 | 80 | 1.28 | 3.9 | 5.52 | 7.84 | 3.39 | 1.06 |
| 20 | 12.64 | 1.24 | 1.84 | 1.38 | 31.2 | 4.25 | 1.47 | 2.5 | 6.08 | 1.32 | 3.53 |
| 21 | 12.92 | 1.37 | 1.9 | 1.55 | 29.49 | 3.98 | 1.62 | 2.58 | 6.83 | 1.25 | 3.31 |
Sheet 8: Влияние коэфициентов
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0.61 | |||||||
| R-квадрат | 0.37 | |||||||
| Нормированный R-квадрат | 0.16 | |||||||
| Стандартная ошибка | 24.47 | |||||||
| Наблюдения | 21 | |||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 5 | 5307.5 | 1061.5 | 1.77 | 0.18 | |||
| Остаток | 15 | 8980.54 | 598.7 | |||||
| Итого | 20 | 14288.04 | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 38.95 | 35.76 | 1.09 | 0.29 | -37.27 | 115.17 | -37.27 | 115.17 |
| Переменная X 1 | 3.83 | 7.11 | 0.54 | 0.6 | -11.32 | 18.98 | -11.32 | 18.98 |
| Переменная X 2 | 1.35 | 6.44 | 0.21 | 0.84 | -12.38 | 15.07 | -12.38 | 15.07 |
| Переменная X 3 | 5.37 | 6.24 | 0.86 | 0.4 | -7.93 | 18.66 | -7.93 | 18.66 |
| Переменная X 4 | -12.44 | 6.8 | -1.83 | 0.09 | -26.94 | 2.07 | -26.94 | 2.07 |
| Переменная X 5 | -12.97 | 5.96 | -2.17 | 0.05 | -25.67 | -0.26 | -25.67 | -0.26 |
| ВЫВОД ОСТАТКА | ||||||||
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки | |||||
| 1 | 36.55 | -34.56 | -1.63 | |||||
| 2 | 19.09 | -6.88 | -0.32 | |||||
| 3 | 36.77 | -13.7 | -0.65 | |||||
| 4 | 34.07 | -9.93 | -0.47 | |||||
| 5 | 26.45 | 8.6 | 0.41 | |||||
| 6 | 27.79 | 9.08 | 0.43 | |||||
| 7 | 37.38 | -32.68 | -1.54 | |||||
| 8 | 40.06 | 18.39 | 0.87 | |||||
| 9 | 19.83 | 39.72 | 1.87 | |||||
| 10 | 54 | 7.42 | 0.35 | |||||
| 11 | 65.63 | -4.12 | -0.19 | |||||
| 12 | 27.74 | 34.21 | 1.61 | |||||
| 13 | 51.86 | 19.38 | 0.91 | |||||
| 14 | 45.03 | 26.42 | 1.25 | |||||
| 15 | 69.53 | 12.35 | 0.58 | |||||
| 16 | 13.61 | -3.53 | -0.17 | |||||
| 17 | 26.71 | -16.46 | -0.78 | |||||
| 18 | 8.42 | 2.39 | 0.11 | |||||
| 19 | 47.52 | -36.43 | -1.72 | |||||
| 20 | 18.34 | -5.7 | -0.27 | |||||
| 21 | 26.87 | -13.95 | -0.66 | |||||
Sheet 9: Анализ Х1
| Коэффициент качества продукции | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X1 | 7 | ||||
| 1.22 | - | 0 | 4 | 1.44 | 5.96 |
| 1.45 | - | 0 | 3 | 1.78 | 8.24 |
| 1.9 | - | 0 | 4 | 2.11 | 9.71 |
| 2.53 | + | 0 | 1 | 2.45 | 9.75 |
| 3.41 | + | 0 | 4 | 2.79 | 8.34 |
| 1.96 | - | 0 | 0 | 3.13 | 6.08 |
| 2.71 | + | 0 | 2 | 3.46 | 3.78 |
| 1.76 | - | 0 | |||
| 2.09 | + | 0 | |||
| 1.1 | - | 0 | |||
| 3.62 | + | 0 | |||
| 3.53 | + | 0 | |||
| 2.09 | + | 0 | |||
| 1.54 | - | 0 | |||
| 2.41 | + | 0 | |||
| 3.64 | + | 0 | |||
| 2.61 | + | 0 | |||
| 2.62 | + | 0 | |||
| 3.29 | + | 0 | |||
| 1.24 | - | 0 | |||
| 1.37 | - | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 2.29 | 1.91 | 2.67 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 0.71 | 0.44 | 1.56 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 0.84 | Критерий серий | Err:502 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 2.09 | 5 | 11 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12.6 | |||
| 2.54 | |||||
| Вариация | Критерий инверсий | ||||
| 37% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 0 | 125 | ||
| 0.29 | тренд отсутствует | ||||
| Эксцес | |||||
| -1.16 | |||||
Sheet 10: Анализ Х2
| Доля в общем объеме продаж | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X2 | 9 | ||||
| 1.24 | - | 0 | 5 | 1.53 | 8.61 |
| 1.54 | - | 0 | 3 | 1.83 | 10.71 |
| 1.31 | - | 0 | 5 | 2.12 | 11.35 |
| 1.36 | - | 0 | 1 | 2.42 | 10.25 |
| 2.65 | + | 0 | 5 | 2.71 | 7.89 |
| 1.63 | - | 0 | 0 | 3.01 | 5.18 |
| 1.66 | - | 0 | 0 | 3.3 | 2.89 |
| 1.4 | - | 0 | 1 | 3.6 | 1.38 |
| 2.61 | + | 0 | 1 | 3.89 | 0.56 |
| 2.42 | + | 0 | |||
| 3.5 | + | 0 | |||
| 1.29 | - | 0 | |||
| 2.44 | + | 0 | |||
| 2.6 | + | 0 | |||
| 2.11 | + | 0 | |||
| 2.06 | + | 0 | |||
| 1.85 | - | 0 | |||
| 2.28 | + | 0 | |||
| 4.07 | + | 0 | |||
| 1.84 | - | 0 | |||
| 1.9 | + | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 2.08 | 1.75 | 2.42 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 0.54 | 0.33 | 1.19 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 0.74 | Критерий серий | 0 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 1.9 | 5 | 10 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12.6 | |||
| 2.83 | |||||
| Вариация | Критерий инверсий | ||||
| 35% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 0 | 125 | ||
| 1.19 | тренд отсутствует | ||||
| Эксцес | |||||
| 1.49 | |||||
Sheet 11: Анализ Х3
| Розничная цена | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X3 | 8 | ||||
| 1.3 | - | 0 | 3 | 1.09 | 15.4 |
| 1.04 | - | 0 | 0 | 1.18 | 24.12 |
| 1 | - | 0 | 4 | 1.27 | 32.2 |
| 1.64 | + | 0 | 3 | 1.36 | 36.63 |
| 1.19 | - | 0 | 2 | 1.45 | 35.52 |
| 1.26 | - | 0 | 1 | 1.54 | 29.34 |
| 1.28 | - | 0 | 3 | 1.64 | 20.65 |
| 1.42 | + | 0 | 4 | 1.73 | 12.39 |
| 1.65 | + | 0 | |||
| 1.24 | - | 0 | |||
| 1.09 | - | 0 | |||
| 1.29 | - | 0 | |||
| 1.65 | + | 0 | |||
| 1.19 | - | 0 | |||
| 1.64 | + | 0 | |||
| 1.46 | + | 0 | |||
| 1.59 | + | 0 | |||
| 1.57 | + | 0 | |||
| 1.78 | + | 0 | |||
| 1.38 | + | 0 | |||
| 1.55 | + | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 1.39 | 1.29 | 1.49 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 0.05 | 0.03 | 0.11 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 0.23 | Критерий серий | 0 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 1.38 | 5 | 8 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12.6 | |||
| 0.78 | |||||
| Вариация | Критерий инверсий | ||||
| 16% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 0 | 125 | ||
| -0.06 | тренд отсутствует | ||||
| Эксцес | |||||
| -1.12 | |||||
Sheet 12: Анализ Х4
| Коэффициент издержек на 1 продукции | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X4 | 5 | ||||
| 35.19 | - | 0 | 5 | 32.76 | 0.21 |
| 80 | + | 11 | 4 | 42.22 | 0.29 |
| 23.31 | - | 0 | 1 | 51.67 | 0.34 |
| 80 | + | 10 | 0 | 61.12 | 0.35 |
| 80 | + | 10 | 1 | 70.58 | 0.3 |
| 68.84 | + | 0 | |||
| 80 | + | 9 | |||
| 30.32 | - | 0 | |||
| 80 | + | 8 | |||
| 32.94 | - | 0 | |||
| 28.56 | - | 0 | |||
| 78.75 | + | 0 | |||
| 38.63 | - | 0 | |||
| 48.67 | - | 0 | |||
| 40.83 | - | 0 | |||
| 80 | + | 2 | |||
| 80 | + | 2 | |||
| 80 | + | 2 | |||
| 80 | + | 2 | |||
| 31.2 | - | 0 | |||
| 29.49 | - | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 57.46 | 46.71 | 68.22 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 558.54 | 343.26 | 1223.07 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 23.63 | Критерий серий | Err:502 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 68.84 | 5 | 11 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12.6 | |||
| 56.69 | |||||
| Вариация | Критерий инверсий | ||||
| 41% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 56 | 125 | ||
| -0.2 | тренд отсутствует | ||||
| Эксцес | |||||
| -1.98 | |||||
Sheet 13: Анализ Х5
| Удовлетворение условий розничных торговцев | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X5 | 8 | ||||
| 2.08 | + | 0 | 3 | 0.62 | 3.83 |
| 1.09 | - | 0 | 3 | 1.1 | 5.47 |
| 2.28 | + | 0 | 3 | 1.58 | 6.67 |
| 1.44 | - | 0 | 3 | 2.06 | 6.93 |
| 1.75 | + | 0 | 4 | 2.55 | 6.13 |
| 1.54 | - | 0 | 1 | 3.03 | 4.62 |
| 0.47 | - | 0 | 0 | 3.51 | 2.97 |
| 2.51 | + | 0 | 3 | 3.99 | 1.63 |
| 2.81 | + | 0 | |||
| 0.59 | - | 0 | |||
| 0.64 | - | 0 | |||
| 1.73 | - | 0 | |||
| 1.83 | + | 0 | |||
| 0.76 | - | 0 | |||
| 0.14 | - | 0 | |||
| 3.53 | + | 0 | |||
| 2.13 | + | 0 | |||
| 3.86 | + | 0 | |||
| 1.28 | - | 0 | |||
| 4.25 | + | 0 | |||
| 3.98 | + | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 1.94 | 1.39 | 2.49 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 1.45 | 0.89 | 3.17 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 1.2 | Критерий серий | 0.07 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 1.75 | 5 | 13 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12.6 | |||
| 4.11 | |||||
| Вариация | Критерий инверсий | ||||
| 62% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 0 | 125 | ||
| 0.53 | тренд отсутствует | ||||
| Эксцес | |||||
| -0.58 | |||||
Overview
Лист1Лист2
Sheet 1: Лист1
| Прибыль | Коэффициент качества продукции | Доля в общем объеме продаж | Розничная цена | Коэффициент издержек на 1 продукции | Удовлетворение условий розничных торговцев | |
| № | Y, % | X1 | X2 | X3 | X4 | X5 |
| 1 | 1.99 | 1.22 | 1.24 | 1.3 | 35.19 | 2.08 |
| 2 | 12.21 | 1.45 | 1.54 | 1.04 | 80 | 1.09 |
| 3 | 23.07 | 1.9 | 1.31 | 1 | 23.31 | 2.28 |
| 4 | 24.14 | 2.53 | 1.36 | 1.64 | 80 | 1.44 |
| 5 | 35.05 | 3.41 | 2.65 | 1.19 | 80 | 1.75 |
| 6 | 36.87 | 1.96 | 1.63 | 1.26 | 68.84 | 1.54 |
| 7 | 4.7 | 2.71 | 1.66 | 1.28 | 80 | 0.47 |
| 8 | 58.45 | 1.76 | 1.4 | 1.42 | 30.32 | 2.51 |
| 9 | 59.55 | 2.09 | 2.61 | 1.65 | 80 | 2.81 |
| 10 | 61.42 | 1.1 | 2.42 | 1.24 | 32.94 | 0.59 |
| 11 | 61.51 | 3.62 | 3.5 | 1.09 | 28.56 | 0.64 |
| 12 | 61.95 | 3.53 | 1.29 | 1.29 | 78.75 | 1.73 |
| 13 | 71.24 | 2.09 | 2.44 | 1.65 | 38.63 | 1.83 |
| 14 | 71.45 | 1.54 | 2.6 | 1.19 | 48.67 | 0.76 |
| 15 | 81.88 | 2.41 | 2.11 | 1.64 | 40.83 | 0.14 |
| 16 | 10.08 | 3.64 | 2.06 | 1.46 | 80 | 3.53 |
| 17 | 10.25 | 2.61 | 1.85 | 1.59 | 80 | 2.13 |
| 18 | 10.81 | 2.62 | 2.28 | 1.57 | 80 | 3.86 |
| 19 | 11.09 | 3.29 | 4.07 | 1.78 | 80 | 1.28 |
| 20 | 12.64 | 1.24 | 1.84 | 1.38 | 31.2 | 4.25 |
| 21 | 12.92 | 1.37 | 1.9 | 1.55 | 29.49 | 3.98 |
Sheet 2: Лист2
| Месяц | 1994 | 1996 | 1997 | 1998 |
| Январь | 1500000 | 1650000 | 1400000 | 1700000 |
| Февраль | 900000 | 850000 | 890000 | 1200000 |
| Март | 700000 | 600000 | 550000 | 459000 |
| Апрель | 300000 | 125000 | 250000 | 221000 |
| Май | 400000 | 300000 | 100000 | 1000 |
| Июнь | 250000 | 450000 | 150000 | 250000 |
| Июль | 200000 | 600000 | 132000 | 325000 |
| Август | 150000 | 750000 | 142000 | 354000 |
| Сентябрь | 300000 | 300000 | 254000 | 150000 |
| Октябрь | 250000 | 259000 | 350000 | 100000 |
| Ноябрь | 400000 | 453000 | 450000 | 259000 |
| Декабрь | 2000000 | 1700000 | 1000000 | 1900000 |