
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология и педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по информатике программированию
Краткое содержание произведений
Реферат: Оптимизация режимов движения судов с использованием MATLAB 5.0
Реферат: Оптимизация режимов движения судов с использованием MATLAB 5.0
Использование операторов polyfit и polyval для аппроксимации кривой
Цель работы.
Получение полинома, описывающего аппроксимированную кривую наиболее близкую к исходной, которая построена по точкам.
Исходные данные.
| x | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
| f(x) | 0 | 80 | 100 | 110 | 120 | 180 | 210 | 230 | 260 |
Программа.
%Исходные данные
x=[0 400 800 1200 1600 2000 2400 2800 3200];
f=[0 80 100 110 120 180 210 230 260];
%a - коэффициенты полинома
%S - квадратичная погрешность
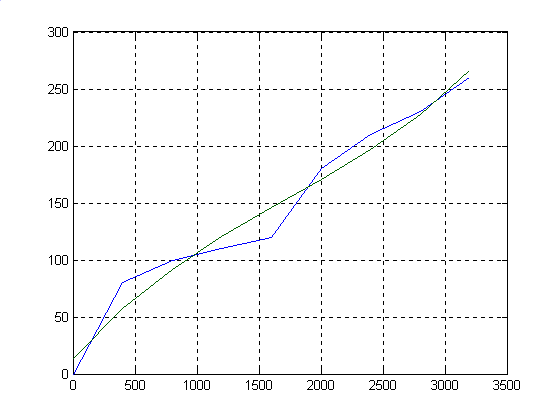
[a,S]=polyfit(x,f,3)
z=polyval(a,x)
%Построение графиков
plot(x,f,x,z),grid
Результат.
a =
0.0000 -0.0000 0.1223 13.5354
S =
R: [4x4 double]
df: 5
normr: 43.1607
z =
Columns 1 through 7
13.5354 57.1717 91.9986 120.6926 145.9307 170.3896 196.7460
Columns 8 through 9
227.6768 265.8586
Командой plot произвели построение исходной функции (синий цвет) и функции аппроксимирующей её (зелёный цвет). Поскольку велико значение погрешности normr=43.1607 и недостаточно аппроксимирование, то следует повысить степень полинома. Пусть вместо 3 будет 6.
Программа.
%Исходные данные
x=[0 400 800 1200 1600 2000 2400 2800 3200];
f=[0 80 100 110 120 180 210 230 260];
%a - коэффициенты полинома
%S - квадратичная погрешность
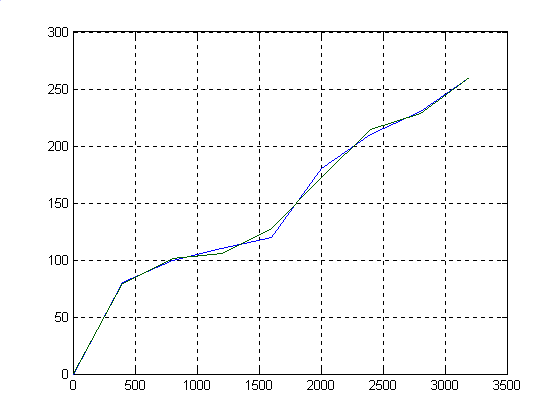
[a,S]=polyfit(x,f,6)
z=polyval(a,x)
%Построение графиков
plot(x,f,x,z),grid
Результат.
a =
0.0000 -0.0000 0.0000 -0.0000 -0.0002 0.2770 0.0140
S =
R: [7x7 double]
df: 2
normr: 12.4672
z =
Columns 1 through 7
0.0140 79.7016 101.6970 105.3007 127.5058 172.6900 214.3077
Columns 8 through 9
228.5828 260.2005
Вывод.
В результате работы видно, что при увеличении степени полинома уменьшается погрешность и аппроксимированная кривая наиболее близка к исходной. В случае когда степень полинома равна количеству исходных точек, получаем: normr=0 и полное соответствие кривых в исходных точках.
Оптимальное распределение двух ресурсов
Цель работы.
Получение максимального значения прибыли при перевозке двух различных грузов.
Исходные данные.
| x | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
|
f1(x) |
0 | 80 | 100 | 110 | 120 | 180 | 210 | 230 | 260 |
|
f2(x) |
0 | 60 | 90 | 110 | 130 | 150 | 190 | 230 | 250 |
f1(x) доход от перевозки груза первого рода;
f2(x) доход от перевозки груза второго рода;
x количество груза.
Программа.
%Исходные данные
x=[0 400 800 1200 1600 2000 2400 2800 3200];
f1=[0 80 100 110 120 180 210 230 260];
f2=[0 60 90 110 130 150 190 230 250];
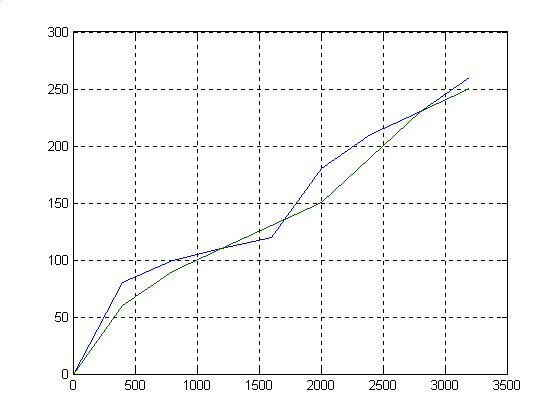
plot(x,f1,x,f2),grid
%Решение
F12=[];
for xR=1:9;
I=1:xR;
L12=f1(I)+f2(xR-I+1);
[Lopt,I]=max(L12);
x1=I*400-400;
x2=(xR-I)*400;
Pacn=[Lopt;x1;x2;x1+x2];
F12=[F12 Pacn];
end
F12
pause
plot(x,F12(1,:)),grid
Результат.
F12 =
Columns 1 through 6
0 80 140 170 190 210
0 400 400 400 400 400
0 0 400 800 1200 1600
0 400 800 1200 1600 2000
Columns 7 through 9
240 270 310
2000 400 400
400 2400 2800
2400 2800 3200
В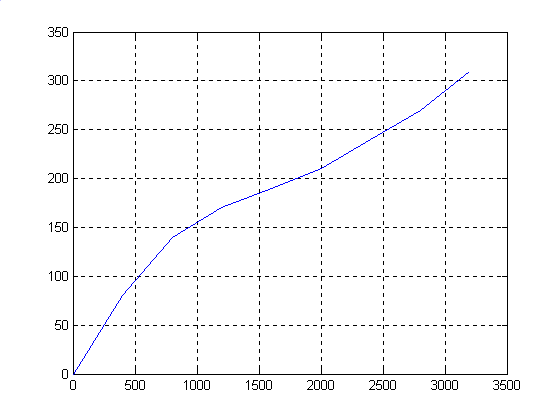 результате
получаем матрицу,
в которой:
результате
получаем матрицу,
в которой:
1 строка суммарный доход от перевозки;
2 строка количество первого груза;
3 строка количество второго груза;
4 строка суммарное количество грузов.
Вывод.
Таким образом получена оптимальная зависимость распределения груза с наибольшим доходом от перевозки. Для наглядности по полученным значениям построен график.
Оптимальное распределение шести ресурсов
Цель работы.
Получение максимального значения прибыли при перевозке шести различных грузов.
Исходные данные.
| x | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
|
f1(x) |
0 | 80 | 100 | 110 | 120 | 180 | 210 | 230 | 260 |
|
f2(x) |
0 | 60 | 90 | 110 | 130 | 150 | 190 | 230 | 250 |
|
f3(x) |
0 | 30 | 40 | 70 | 110 | 180 | 200 | 240 | 250 |
|
f4(x) |
0 | 40 | 60 | 80 | 130 | 160 | 180 | 210 | 240 |
|
f5(x) |
0 | 50 | 70 | 90 | 110 | 150 | 170 | 200 | 220 |
|
f6(x) |
0 | 70 | 80 | 110 | 140 | 160 | 200 | 250 | 270 |
f1(x) доход от перевозки груза первого рода;
f2(x) доход от перевозки груза второго рода;
f3(x) доход от перевозки груза третьего рода;
f4(x) доход от перевозки груза четвёртого рода;
f5(x) доход от перевозки груза пятого рода;
f6(x) доход от перевозки груза шестого рода;
x количество груза.
Программа.
%Исходные данные
x=[0 400 800 1200 1600 2000 2400 2800 3200];
f1=[0 80 100 110 120 180 210 230 260];
f2=[0 60 90 110 130 150 190 230 250];
f3=[0 30 40 70 110 180 200 240 250];
f4=[0 40 60 80 130 160 180 210 240];
f5=[0 50 70 90 110 150 170 200 220];
f6=[0 70 80 110 140 160 200 250 270];
F=[f1;f2;f3;f4;f5;f6];
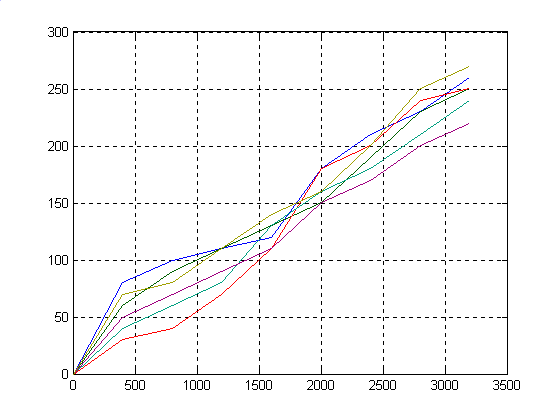
plot(x,F),grid
%Решение
FF=[];
J=1;
for XR=1:9;
I=1:XR;
L=F(J,I)+F(J+1,XR-I+1);
[Lopt,I]=max(L);
x1=I*400-400;
x2=(XR-I)*400;
Pacn=[Lopt;x1;x2;x1+x2];
FF=[FF Pacn];
end
D=FF(1,:);
PP=[];
RRR=[];
for J=2:5;
DD=[];
RR=[];
for XR=1:9;
I=1:XR;
L=D(I)+F(J+1,XR-I+1);
[Lopt,I]=max(L);
x1=I*400-400;
x2=(XR-I)*400;
Pacn=[Lopt;x1;x2;x1+x2];
DD=[DD Pacn(1,:)];
 RR=[RR Pacn];
RR=[RR Pacn];
end
PP=[PP;DD(1,:)];
RRR=[RRR RR];
D=DD;
end
RRR=[FF RRR]
pause
plot(x,RRR(1,37:45)),grid
Результат.
RRR =
Columns 1 through 6
0 80 140 170 190 210
0 400 400 400 400 400
0 0 400 800 1200 1600
0 400 800 1200 1600 2000
Columns 7 through 12
240 270 310 0 80 140
2000 400 400 0 400 800
400 2400 2800 0 0 0
2400 2800 3200 0 400 800
Columns 13 through 18
170 200 220 260 320 350
800 1200 1600 400 800 1200
400 400 400 2000 2000 2000
1200 1600 2000 2400 2800 3200
Columns 19 through 24
0 80 140 180 210 240
0 400 800 800 1200 1600
0 0 0 400 400 400
0 400 800 1200 1600 2000
Columns 25 through 30
270 320 360 0 80 140
800 2800 2800 0 400 800
1600 0 400 0 0 0
2400 2800 3200 0 400 800
Columns 31 through 36
190 230 260 290 320 370
800 1200 1600 2000 2400 2800
400 400 400 400 400 400
1200 1600 2000 2400 2800 3200
Columns 37 through 42
0 80 150 210 260 300
0 400 400 800 1200 1600
0 0 400 400 400 400
0 400 800 1200 1600 2000
Columns 43 through 45
330 360 390
2000 2400 2800
400 400 400
2400 2800 3200
В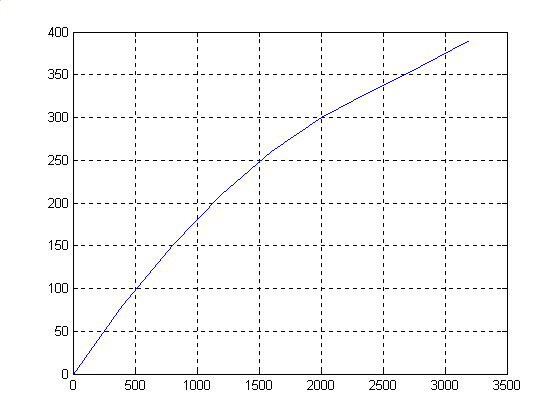 результате
получаем матрицу,
в которой:
результате
получаем матрицу,
в которой:
1 строка доход от перевозки i грузов;
2 строка
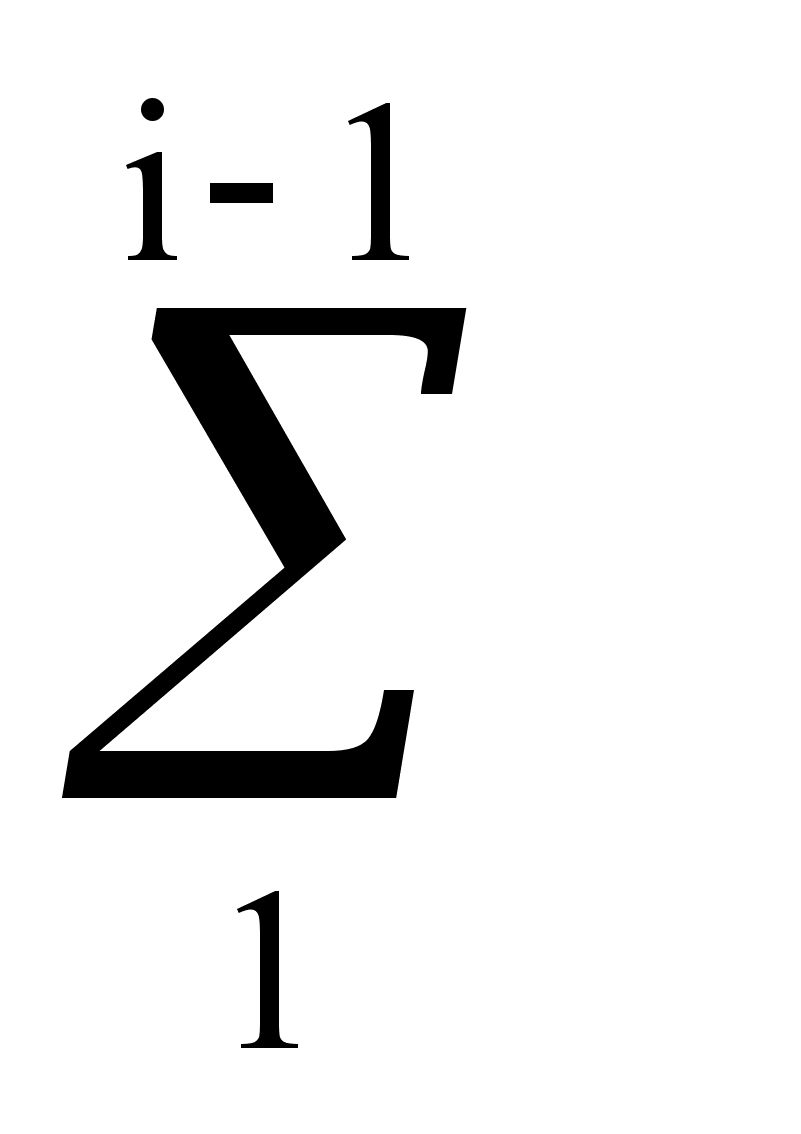 количества
грузов;
количества
грузов;3 строка количество i-ого груза;
4 строка суммарное количество грузов.
Вывод.
Таким образом получена оптимальная зависимость распределения груза с наибольшим доходом от перевозки. Для наглядности по полученным значениям построен график.
Оптимизация режима движения судна
Цель работы.
Распределить скорость движения судна по четырём участкам трассы так, чтобы суммарный расход топлива был минимальным.
Программа.
%Подготовка исходных данных
delt=0.07;
tmin=[5.86 2.73 1.6 3.3967]; tmax=[7.47 3.71 2.37 4.5167];
t=[tmin; tmax]; tb=[tmax-tmin];
G1=[967.42 941.39 912 892.29 878.02 846.11 823.73 798.51 775.22 ...
764.2 741.28 719.36 706.85 678.15 673.74 659.91 645.65 ...
630.98 623 610.9 598.95 590.07 577.2 571.46];
G2=[521.73 491.12 463.51 437.33 415.2 392.7 377.45 358.23 346.86 ...
328.98 316.25 305.38 295.48 285.86 277.11];
G3=[281.47 255.5 231.07 210.41 192.31 177.55 166.97 157.77 ...
149.86 144.48 140.91 139.23];
G4=[590.60 561.90 535.10 510.20 487.06 465.67 445.94 427.82 ...
411.23 396.12 382.42 370.06 358.99 349.13 340.42 332.80 325.41];
%Формирование векторов t1, t2, t3, t4
t1=t(1,1):delt:t(2,1);
t2=t(1,2):delt:t(2,2);
t3=t(1,3):delt:t(2,3);
t4=t(1,4):delt:t(2,4);
%Пригонка данных
[a1,H1]=polyfit(t1,G1,3);
[a2,H2]=polyfit(t2,G2,3);
[a3,H3]=polyfit(t3,G3,3);
[a4,H4]=polyfit(t4,G4,3);
a=[a1;a2;a3;a4];
%Апроксимация исходных зависимостей
N=25;
deltM=tb./(N-1);
%Моделирование
TM=[];Gm=[];
for i=1:4;
tm=t(1,i):deltM(i):t(2,i);
TM=[TM;tm];
gm=polyval(a(i,:),tm);
Gm=[Gm;gm];
end
deltt=deltM;
%Оптимизация распределения времени движения
GG=[];
F=Gm;
for xr=1:N;
I=1:xr;
L=Gm(1,I)+Gm(2,xr-I+1);
[Lopt,I]=min(L);
X1=5.86+I*deltt(1)-deltt(1);
X2=2.73+(xr-I)*deltt(2);
Pacn=[Lopt.*0.001;X1;X2;X1+X2];
GG=[GG Pacn];
end
D=GG(1,:);
C=GG(4,:);
PP=[];RRR=[];
for J=2:3;
DD=[];RR=[];CC=[];
for xr=1:N;
I=1:xr;
L=D(I)+0.001.*F(J+1,xr-I+1);
[Lopt,I]=min(L);
X1=C(I);
X2=TM(J+1,1)+(xr-I)*deltt(J+1);
Pacn=[Lopt;X1;X2;X1+X2];
DD=[DD Pacn(1,:)];
RR=[RR Pacn];
CC=[CC Pacn(4,:)];
end
PP=[PP;DD(1,:)];
RRR=[RRR RR];
D=DD;
C=CC;
end
RRR=[GG RRR];
R12=RRR(:,1:N)
R23=RRR(:,N+1:2*N)
R34=RRR(:,2*N+1:3*N)
plot(R34(1,:),R34(4,:)),grid
Результат.
R12 =
Columns 1 through 7
1.4899 1.4647 1.4402 1.4164 1.3934 1.3710 1.3494
5.8600 5.9271 5.9942 6.0613 6.1283 6.1954 6.2625
2.7300 2.7300 2.7300 2.7300 2.7300 2.7300 2.7300
8.5900 8.6571 8.7242 8.7912 8.8583 8.9254 8.9925
Columns 8 through 14
1.3285 1.3083 1.2889 1.2703 1.2522 1.2343 1.2172
6.3296 6.3967 6.4638 6.5308 6.5308 6.5979 6.5979
2.7300 2.7300 2.7300 2.7300 2.7708 2.7708 2.8117
9.0596 9.1267 9.1937 9.2608 9.3017 9.3688 9.4096
Columns 15 through 21
1.2001 1.1838 1.1675 1.1521 1.1367 1.1220 1.1075
6.6650 6.7321 6.7321 6.7992 6.7992 6.8663 6.8663
2.8117 2.8117 2.8525 2.8525 2.8933 2.8933 2.9342
9.4767 9.5437 9.5846 9.6517 9.6925 9.7596 9.8004
Columns 22 through 25
1.0936 1.0799 1.0668 1.0538
6.9333 6.9333 7.0004 7.0004
2.9342 2.9750 2.9750 3.0158
9.8675 9.9083 9.9754 10.0162
R23 =
Columns 1 through 7
1.7720 1.7468 1.7223 1.6985 1.6754 1.6530 1.6314
8.5900 8.6571 8.7242 8.7912 8.8583 8.9254 8.9925
1.6000 1.6000 1.6000 1.6000 1.6000 1.6000 1.6000
10.1900 10.2571 10.3242 10.3912 10.4583 10.5254 10.5925
Columns 8 through 14
1.6105 1.5904 1.5710 1.5523 1.5342 1.5164 1.4992
9.0596 9.1267 9.1937 9.2608 9.3017 9.3688 9.4096
1.6000 1.6000 1.6000 1.6000 1.6000 1.6000 1.6000
10.6596 10.7267 10.7937 10.8608 10.9017 10.9688 11.0096
Columns 15 through 21
1.4821 1.4658 1.4496 1.4341 1.4187 1.4040 1.3895
9.4767 9.5437 9.5846 9.6517 9.6925 9.7596 9.8004
1.6000 1.6000 1.6000 1.6000 1.6000 1.6000 1.6000
11.0767 11.1437 11.1846 11.2517 11.2925 11.3596 11.4004
Columns 22 through 25
1.3756 1.3619 1.3488 1.3358
9.8675 9.9083 9.9754 9.9754
1.6000 1.6000 1.6000 1.6321
11.4675 11.5083 11.5754 11.6075
R34 =
Columns 1 through 7
2.3626 2.3374 2.3129 2.2892 2.2661 2.2437 2.2221
10.1900 10.2571 10.3242 10.3912 10.4583 10.5254 10.5925
3.3967 3.3967 3.3967 3.3967 3.3967 3.3967 3.3967
13.5867 13.6538 13.7209 13.7879 13.8550 13.9221 13.9892
Columns 8 through 14
2.2012 2.1810 2.1616 2.1422 2.1236 2.1051 2.0870
10.6596 10.7267 10.7267 10.7937 10.8608 10.8608 10.9017
3.3967 3.3967 3.4434 3.4434 3.4434 3.4900 3.4900
14.0563 14.1234 14.1700 14.2371 14.3042 14.3509 14.3917
Columns 15 through 21
2.0691 2.0514 2.0343 2.0172 2.0004 1.9841 1.9678
10.9688 10.9688 11.0096 11.0767 11.0767 11.1437 11.1846
3.4900 3.5367 3.5367 3.5367 3.5834 3.5834 3.5834
14.4588 14.5055 14.5463 14.6134 14.6600 14.7271 14.7679
Columns 22 through 25
1.9518 1.9363 1.9209 1.9057
11.1846 11.2517 11.2925 11.2925
3.6300 3.6300 3.6300 3.6767
14.8146 14.8817 14.9225 14.9692
В результате получаем матрицы, в которых:
1 строка расход топлива на участках;
2 строка время движения по предыдущим участкам;
3 строка время движения по i-тому участку;
4 строка суммарное время движения по участкам.
R12 результаты для двух участков;
R23 результаты для трёх участков;
R34 результаты для четырёх участков;
Вывод.
 В
качестве вывода
приведена
графическая
зависимость
расхода топлива
(ось абсцисс)
от времени
прохождения
всех участков
(ось ординат).
В
качестве вывода
приведена
графическая
зависимость
расхода топлива
(ось абсцисс)
от времени
прохождения
всех участков
(ось ординат).
Оптимальные режимы работы судовых генераторных агрегатов
Цель работы.
Найти оптимальное распределение мощности между дизель-генераторами.
Программа.
%Исходные данные
delt=10;
P1=0:delt:50;
P2=0:delt:70;
P3=0:delt:80;
F1=(0.03*(P1.^2)+2*P1+80);
F2=(0.015*(P2.^2)+1.45*P2+100);
F3=(0.01*(P3.^2)+0.95*P3+120);
%Решение
for T=1:2;
r1=size(F1);
r2=size(F2);
if r1(2)
N=r1(2);M=r2(2);
else
N=r2(2);M=r1(2);
end
[x,y]=meshgrid(F1,F2);
z=x+y;
M
N
X=rot90(z,3);
XX=[];IM=[];IM3=[];
for cc=-(N-1):(M-1);
[v,I]=min(diag(X,cc));
XX=[XX v];
if cc
IM3=[IM3 abs(cc-I)];
else
IM=[IM I];
end
IMM=[IM3 IM];
end
X1=rot90(XX,2);
IM1=rot90(IMM,2);
Opt1=[X1;IM1.*delt-delt];
r=size(X1);
v1=1:r(2);
P=v1.*delt;
Opt2=[Opt1;P-delt];
Opt=[Opt2(1,:);Opt2(2,:);Opt2(3,:)-Opt2(2,:);Opt2(3,:)]
F2=Opt(1,:);
F1=F3;
end
Результат.
M =
8
N =
6
Opt =
180 196 215 237 260 285 313 342 373 407 442 483 530
0 0 0 0 10 10 10 20 20 20 30 40 50
0 10 20 30 30 40 50 50 60 70 70 70 70
0 10 20 30 40 50 60 70 80 90 100 110 120
M =
13
N =
9
Opt =
Columns 1 through 7
300.0000 310.5000 323.0000 337.5000 353.5000 370.0000 388.5000
0 10.0000 20.0000 30.0000 30.0000 40.0000 50.0000
0 0 0 0 10.0000 10.0000 10.0000
0 10.0000 20.0000 30.0000 40.0000 50.0000 60.0000
Columns 8 through 14
407.5000 428.0000 450.0000 472.5000 495.5000 520.0000 545.0000
50.0000 60.0000 60.0000 70.0000 70.0000 80.0000 80.0000
20.0000 20.0000 30.0000 30.0000 40.0000 40.0000 50.0000
70.0000 80.0000 90.0000 100.0000 110.0000 120.0000 130.0000
Columns 15 through 21
573.0000 602.0000 633.0000 667.0000 702.0000 743.0000 790.0000
80.0000 80.0000 80.0000 80.0000 80.0000 80.0000 80.0000
60.0000 70.0000 80.0000 90.0000 100.0000 110.0000 120.0000
140.0000 150.0000 160.0000 170.0000 180.0000 190.0000 200.0000
Также существует второй метод решения этой задачи, который представлен в программе ниже.
Программа.
%Исходные данные
delt=10;
P1=0:delt:50;
P2=0:delt:70;
P3=0:delt:80;
F1=(0.03*(P1.^2)+2*P1+80);
F2=(0.015*(P2.^2)+1.45*P2+100);
F3=(0.01*(P3.^2)+0.95*P3+120);
%Решение
FA=F1; FB=F2;
for j=1:2;
e1=size(FA); N=e1(2);
e2=size(FB); M=e2(2);
[x,y]=meshgrid(FA,FB);
z=x+y
Dmin=[]; D1min=[]; D2min=[];
Im=[]; I1m=[]; I2m=[];
for k=1:M+N-1;
if k
DD=[];
for i=k:-1:1;
g=z(i,k-i+1);
DD=[DD g];
end
[L,I]=min(DD);
Dmin=[Dmin L];
Im=[Im I];
elseif (N
DD1=[];
for i1=k:-1:k-N+1;
g1=z(i1,k-i1+1);
DD1=[DD1 g1];
end
[L1,I1]=min(DD1);
D1min=[D1min L1];
I1m=[I1m I1];
elseif (M
DD2=[];
for i2=M:-1:k-N+1;
g2=z(i2,k-i2+1);
DD2=[DD2 g2];
end
[L2,I2]=min(DD2);
D2min=[D2min L2];
I2m=[I2m k-M+I2];
end
end
F12=[Dmin D1min D2min]
I11=[Im I1m I2m];
r=size(F12);
v=1:r(2);
P=v.*delt;
Opt=[F12;I11.*delt-delt;P-delt];
Optim12=[Opt(1,:);Opt(2,:);Opt(3,:)-Opt(2,:);Opt(3,:)]
FB=Optim12(1,:);
FA=F3;
end
Результат.
z =
180 203 232 267 308 355
196 219 248 283 324 371
215 238 267 302 343 390
237 260 289 324 365 412
262 285 314 349 390 437
290 313 342 377 418 465
321 344 373 408 449 496
355 378 407 442 483 530
F12 =
180 196 215 237 260 285 313 342 373 407 442 483 530
Optim12 =
180 196 215 237 260 285 313 342 373 407 442 483 530
0 0 0 0 10 10 10 20 20 20 30 40 50
0 10 20 30 30 40 50 50 60 70 70 70 70
0 10 20 30 40 50 60 70 80 90 100 110 120
z =
Columns 1 through 7
300.0000 310.5000 323.0000 337.5000 354.0000 372.5000 393.0000
316.0000 326.5000 339.0000 353.5000 370.0000 388.5000 409.0000
335.0000 345.5000 358.0000 372.5000 389.0000 407.5000 428.0000
357.0000 367.5000 380.0000 394.5000 411.0000 429.5000 450.0000
380.0000 390.5000 403.0000 417.5000 434.0000 452.5000 473.0000
405.0000 415.5000 428.0000 442.5000 459.0000 477.5000 498.0000
433.0000 443.5000 456.0000 470.5000 487.0000 505.5000 526.0000
462.0000 472.5000 485.0000 499.5000 516.0000 534.5000 555.0000
493.0000 503.5000 516.0000 530.5000 547.0000 565.5000 586.0000
527.0000 537.5000 550.0000 564.5000 581.0000 599.5000 620.0000
562.0000 572.5000 585.0000 599.5000 616.0000 634.5000 655.0000
603.0000 613.5000 626.0000 640.5000 657.0000 675.5000 696.0000
650.0000 660.5000 673.0000 687.5000 704.0000 722.5000 743.0000
Columns 8 through 9
415.5000 440.0000
431.5000 456.0000
450.5000 475.0000
472.5000 497.0000
495.5000 520.0000
520.5000 545.0000
548.5000 573.0000
577.5000 602.0000
608.5000 633.0000
642.5000 667.0000
677.5000 702.0000
718.5000 743.0000
765.5000 790.0000
F12 =
Columns 1 through 7
300.0000 310.5000 323.0000 337.5000 353.5000 370.0000 388.5000
Columns 8 through 14
407.5000 428.0000 450.0000 472.5000 495.5000 520.0000 545.0000
Columns 15 through 21
573.0000 602.0000 633.0000 667.0000 702.0000 743.0000 790.0000
Optim12 =
Columns 1 through 7
300.0000 310.5000 323.0000 337.5000 353.5000 370.0000 388.5000
0 10.0000 20.0000 30.0000 30.0000 40.0000 50.0000
0 0 0 0 10.0000 10.0000 10.0000
0 10.0000 20.0000 30.0000 40.0000 50.0000 60.0000
Columns 8 through 14
407.5000 428.0000 450.0000 472.5000 495.5000 520.0000 545.0000
50.0000 60.0000 60.0000 70.0000 70.0000 80.0000 80.0000
20.0000 20.0000 30.0000 30.0000 40.0000 40.0000 50.0000
70.0000 80.0000 90.0000 100.0000 110.0000 120.0000 130.0000
Columns 15 through 21
573.0000 602.0000 633.0000 667.0000 702.0000 743.0000 790.0000
80.0000 80.0000 80.0000 80.0000 80.0000 80.0000 80.0000
60.0000 70.0000 80.0000 90.0000 100.0000 110.0000 120.0000
140.0000 150.0000 160.0000 170.0000 180.0000 190.0000 200.0000
Вывод.
В итоге работы получены одинаковые результаты решения данной задачи при помощи двух методов её решения. Цель работы выполнена.
Разложение периодической функции в ряд Фурье
Цель работы.
Разложить имеющийся периодический сигнал в ряд Фурье.
Исходные данные.
Исходным является сигнал представлен на рисунке.
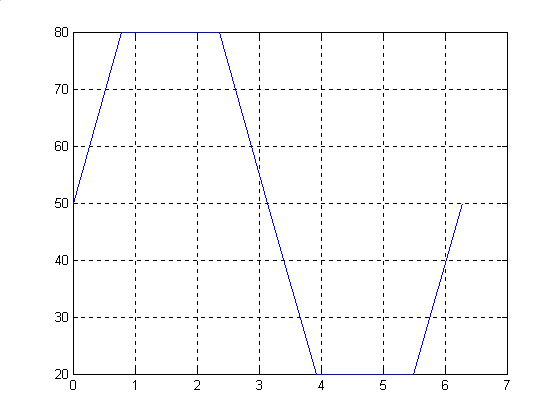
Программа.
U1=[];U2=[];U3=[];
U4=[];U5=[];U6=[];
for Wt=0:0.002*pi:2*pi;
Um=50;a=pi/2;
uu=Um+(4*Um/(a*pi))*(sin(a)*sin(Wt)+(1/9)*sin(3*a)*sin(3*Wt)+(1/25)*sin(5*a)*sin(5*Wt)+(1/49)*sin(7*a)*sin(7*Wt));
U6=[U6 uu];
if 0
u=50+(50/(pi/2))*Wt;
U1=[U1 u];
elseif (pi/2)
u=50+50-(50/(pi/2))*(Wt-pi/2);
U2=[U2 u];
else
u=50-50+(50/(pi/2))*(Wt-(3/2)*pi);
U3=[U3 u];
end
U=[U1 U2 U3];
U6;
end
Wt=0:0.002*pi:2*pi;
plot(Wt,U,Wt,U6),grid
Результат.
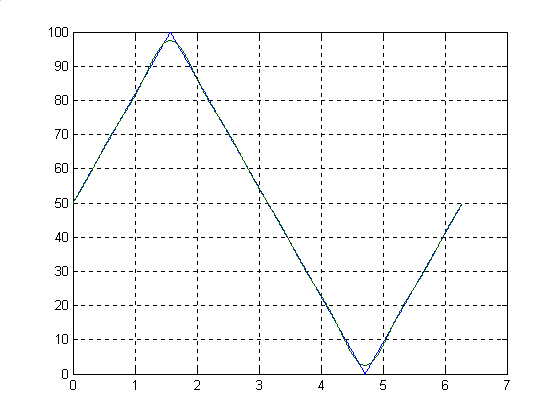
Вывод.
В работе выполнено разложение исходного сигнала в сумму гармоник, график которой представлен в результатах.
Разложение периодической функции в ряд Фурье
Цель работы.
Разложить имеющийся периодический сигнал в ряд Фурье.
Исходные данные.
Исходным является сигнал представлен на рисунке.
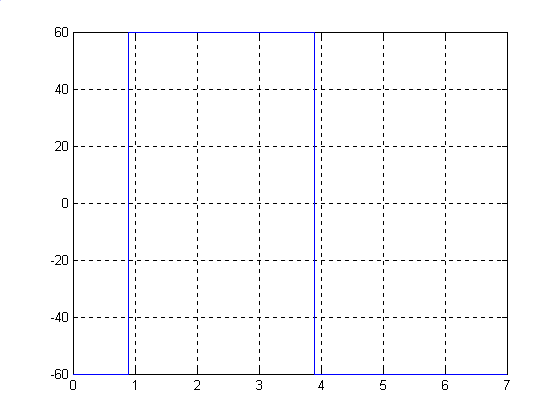
Программа.
F=[];
for k=1:2:21;
Im=60;
wt=0:0.02:7;
i=(4*Im/pi)*((1/k)*sin(k*(wt-pi/4)));
F=[F i'];
end
F1=F';
d=size(F1);
d(1);
F2=sum(F1);
plot(wt,F2,'b'),grid
Р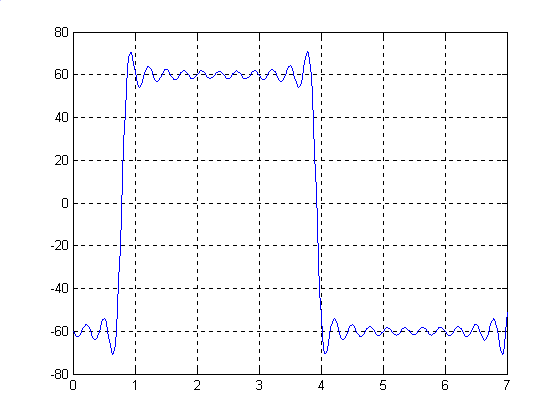 езультат.
езультат.
Программа.
F=[];
for k=1:2:2001;
Im=60;
wt=0:0.02:7;
i=(4*Im/pi)*((1/k)*sin(k*(wt-pi/4)));
F=[F i'];
end
F1=F';
d=size(F1);
d(1);
F2=sum(F1);
plot(wt,F2,'b'),grid
Р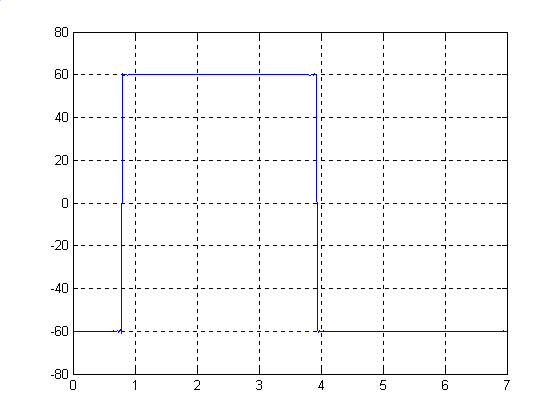 езультат.
езультат.
Вывод.
В данной работе выполнено разложение исходного сигнала на сумму гармоник. В работе показано, что при увеличении числа гармоник их сумма гармоник наиболее приближена к исходному сигналу.
Введение
В последнее время на фоне развития грузопассажирского флота и создании высокопроизводительных судов наблюдается непрерывное стремление по направлению повышения эффективности энергетической установки с целью увеличения экономичности, надёжности и безопасности перевозок.
Судовая энергетическая установка является сложным комплексом различных механизмов, устройств и систем, обеспечивающим движение судна, работу механизмов машинного отделения и палубных механизмов, выработку электроэнергии и т.д.
В связи с развитием электронно-вычислительной техники возможно решение задач экономии топливных ресурсов, оптимизации управления режимами движения судов при различных условиях (ветро-волновое сопротивление, перепады глубин и т.п.) не только технологическим совершенствованием судовой энергетической установки, но и при помощи компьютерных программ.
В данном отчёте приведены примеры программ, составленные в оболочке MATLAB, решающие некоторые вышеуказанные проблемы.

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ВОДНЫХ КОММУНИКАЦИЙ
Отчёт о выполнении лабораторных работ по дисциплине
“Оптимизация режимов движения судов”.
Группа: СЭ-51
Выполнил: Жданов Д. А.
Проверил: Сахаров В. В.
Санкт-Петербург
2001