Реферат: Жидкие растворы

Реферат: Жидкие растворы

СПб ГИТМО (ТУ)

Кафедра: Физической химии,

волокнистой и интегральной оптики.

Реферат

Жидкие растворы.

Студент: Тулякова М. 156гр.

Преподаватель: Успенская М.В.

Санкт- Петербург

2002г

Оглавление:

Оглавление: 2

Вступление 2

I.Определение раствора. 3

II.Процесс растворения 5

III.Классификации растворов. 6

IV.Способы выражения состава растворов 7

V.Растворимость. Зависимость растворимости от температуры. 9

VI.Теплоты растворения и разбавления. 11

VII.Давление пара растворов. Состав пара растворов. 11

VIII.Неидеальные растворы. 14

IX.Активность и коэффици­ент активности. 15

X.Кристаллизация растворов. 16

XI.Кипение растворов. 17

XII.Осмос. 17

Список литературы 19

Вступление

Растворы находят широкое применение в самых различных областях практики. Категории растворов относятся и природный раствор воды, и такие материалы, как сырая нефть и различные нефтепродукты-бензины, керосин, вазелин, парафин, смазочные масла, жидкие сплавы металлов, расплавленные смеси силикатов смеси органических растворителей, различные водноспиртовые смеси и др.

Во второй половине прошлого века существовало две противоположных точки зрения на процесс растворения. Для первой точки зрения характерно рассмотрение процесса растворения как явления химического, для второго - как физического. В химических теориях предполагалось, что растворенное вещество и растворитель химически взаимодействуют между собой. С физической точки зрения растворенное вещество можно рассматривать, как находящееся в газообразном состоянии и применять к нему законы кинетической теории газов. Каждая из этих теорий была разработана и внесла свой вклад в создание современной теории растворов, в которой принимаются во внимание и химические, и физические факторы.

В развитии учения о растворах выдающаяся роль принадлежит работам Д.И. Менделеева. Он рассматривал растворы как неустойчивые химические соединения постоянного состава, находящиеся в состоянии частичной диссоциации. Этим было положено начало химической теории растворов в противовес физическим теориям, игнорировав­шим значение химического взаимодействия.

Общей теории растворов - теории, которая давала бы возмож­ность определять свойства раствора по известным свойствам ком­понентов в чистом состоянии и известному составу раствора, - в настоящее время еще нет. Только для растворов очень разбавленных (в пределе беско­нечно разбавленных) удалось еще в 80-х годах прошлого века со­здать начала количественной теории, дающей возможность опре­делять некоторые свойства растворов по известной их концен­трации. В таких растворах молекулы растворенного вещества разобщены друг от другого большим количеством молекул растворителя. Вследствие этого их взаимодействие не проявляется в заметной степени.

I.Определение раствора.

Растворы - однородная многокомпонентная система, состоящая из растворителя, растворённых веществ и продуктов их взаимодействия, относительные количества которых могут изменяться в широких пределах. Этот термин может относиться к любому агрегатному состоянию системы. По агрегатному состоянию растворы могут быть жидкими (морская вода), газообразными (смеси азота с аммиаком) или твёрдыми (многие сплавы металлов).

Газообразные растворы обычно представляют собой смеси газов и реже – растворы жидкостей или твердых тел в газах. Газы способны смешиваться во всех отношениях не при любых условиях. При высоких температурах и давлении наблюдается неполное смешение газов с образованием двух газообразных фаз, находящихся в равновесии.

Твердые растворы образуются кристаллизации жидких расплавов или при растворении газов в твердых веществах. Различают твердые растворы замещения, внедрения и вычитания.

Твердые растворы замещения, которые образуются при сохранении структуры кристаллической решетки растворителя являются наиболее распространенными. При образовании твердых растворов замещения в узлах кристаллической решетки данного вещества атомы, молекулы и ионы замещаются частицами другого вещества. Образование таких растворов возможно, если оба вещества близки по кристаллическим свойствам и размерам частиц. По приближенному правилу В.Юм-Розери твердые растворы замещения образуются в тех случаях, когда размеры двух частиц отличаются не более чем на 14-15%. Устойчивыми являются твердые растворы замещения любого состава.

Твердые растворы внедрения получаются путем внедрения частиц одного вещества в междоузлия кристаллической решетки другого вещества (растворителя). Растворы внедрения образуются в том случае, когда размеры частиц внедряемого вещества меньше размеров частиц растворителя. Такие растворы обычно возникают при растворении растворов неметаллов в металлах. При внедрении новых частиц в промежутки между атомами металла происходит увеличение напряжения в кристаллической решетке, в связи с такие растворы образуются сравнительно редко.

Твердые растворы вычитания встречаются значительно реже. Они получаются при выпадении некоторых атомов из кристаллической ячейки, в связи с чем эти растворы иногда называются твердыми растворами с дефектной решеткой.

Наиболее часто встречаются жидкие растворы. В моем реферате речь пойдет преимущественно о жидких растворах.

Растворы занимают промежуточное место между химическими соединениями и механическими смесями. Однородность растворов делает их схожими с химическими соединениями, так же на химическое взаимодействие между компонентами растворов указывает выделение теплоты при растворении некоторых веществ. Растворы отличаются от химических соединений тем, что состав взаимодействующих веществ может изменяться в широких пределах. В свойствах раствора можно обнаружить многие свойства компонентов его составляющих, что характерно для механических соединений.

II.Процесс растворения

Процесс растворения кристалла в жидкости происходит так. Когда кристалл соли, например, хлорида натрия попадает в воду, то распложенные на его поверхности ионы притягивают полярные молекулы воды (ион-дипольное взаимодействие). К ионам натрия молекулы притягиваются своими отрицательными полюсами, а к ионам хлора положительными. Но если ионы протягивают к себе молекулы воды, то и молекулы воды притягивают к себе ионы. В то же время притянутые молекулы воды испытывают толчки со стороны непритянутых молекул воды, находящихся в тепловом движении. И этих толчков, а так же тепловых колебаний самих ионов достаточно для того, чтобы ион хлора или натрия отделился от кристалла и перешел в раствор. Вслед за первым слоем ионов в раствор переходит следующий слой и таким образом идет постепенное растворение кристалла. Перешедшие в раствор ионы остаются связанными с молекулами воды и образуют гидраты ионов. Гидратация – основная причина диссоциации . Она отчасти затрудняет их обратное соединение (ассоциацию). Под гидратацией обычно понимают совокупность энергетических процессов и структурных изменений, происходящих в растворе при взаимодействии частиц растворенного вещества с водой. Слой частиц воды, непосредственно присоединенных к центральной частице растворенного вещества образует вокруг нее гдратную оболочку. Наименьшее число молекул растворителя, удерживаемое около частицы растворенного вещества называется координатным числом гидратации. Координатное число определить трудно, оно зависит от природы растворенного вещества и растворителя.

Доказательством того, что компоненты раствора химически взаимодействуют друг с другом, служит тот факт, что многие вещества выделяются из водных растворов в виде кристаллов, содержащих кристаллизованную воду – гидратов; причем на каждую молекулу растворенного вещества приходится определенное число молекул воды. Как правило, гидраты – нестойкие соединения, во многих случаях они разлагаются уже при выпаривании растворов. Но иногда гидраты так прочны, что при выделении растворенного вещества из раствора вода входит в состав его кристаллов. Вещества, в состав которых входят молекулы воды называются кристаллогидратами, а содержащаяся в них вода - кристаллизованной. Прочность связи между гидратами и кристаллизованной водой различна. Многие из них теряют кристаллизованную воду уже при комнатной температуре, для некоторых требуется значительное нагревание, а от кристаллогидрата алюминия, например, не удается удалить воду никакими способами.

Состав кристаллогидратов принято изображать формулами, показывающими, какое количество кристаллизованной воды содержит кристаллогидрат. Например, кристаллогидрат сульфата натрия, содержащий на один моль Na2SO4 10 молей воды выражается формулой Na2SO410H2O.

Иначе протекает диссоциация молекул, которые обладают полярной связью. Молекулы воды, притянувшиеся к концам полярной молекулы (диполь-дипольное взаимодействие), вызывают расхождение ее полюсов – поляризуют молекулу. Такая поляризация в сочетании с колебательным движением атомов в самой молекуле, а так же беспорядочное тепловое движение окружающих ее молекул воды приводит к распаду полярной молекулы на ионы. Как и в случае растворения кристалла с ионной связью эти ионы гидрируются.

Гидрированные ионы содержат как постоянное, так и переменное количество молекул воды, это количество зависит от концентрации и других условий. Гидрат постоянного состава образует ион водорода H+, он называется ионом гидроксония. Ион гидроксония благодаря очень маленьким размерам обладает электростатическим полем большой электороотицательности. Он не имеет электронной оболочки и поэтому не испытывает отталкивания от электронных оболочек других атомов. Поэтому в растворах ион гидроксония существует исключительно в виде объединений с молекулами воды. Самый прочный комплекс образуется с одной молекулой воды, который так же окружается гидратной оболочкой из других молекул.

III.Классификации растворов.

Существует несколько способов классификации растворов. Так, основываясь на величине электрической проводимости, различают растворы электролитов и неэлектролитов. Можно классифицировать растворы по агрегатному состоянию системы и тех частиц, из которых она состоит.

Возможна классификация раствора по количеству растворенного вещества в нем присутствующего. Если молекулярные или ионные частицы, распределённые в жидком растворе, присутствуют в нём в таком количестве, что при данных условиях не происходит дальнейшего растворения вещества, раствор называется насыщенным. (Например, если поместить 50 г NaCl в 100 г H2O, то при 20єC растворится только 36 г соли). Насыщенным называется раствор, который находится в динамическом равновесии с избытком растворённого вещества. Поместив в 100 г воды при 20єC меньше 36 г NaCl мы получим ненасыщенный раствор. При нагревании смеси соли с водой до 100○C произойдёт растворение 39,8 г NaCl в 100 г воды. Если теперь удалить из раствора нерастворившуюся соль, а раствор осторожно охладить до 20єC, избыточное количество соли не всегда выпадает в осадок. В этом случае мы имеем дело с перенасыщенным раствором. Перенасыщенные растворы очень неустойчивы. Помешивание, встряхивание, добавление крупинок соли может вызвать кристаллизацию избытка соли и переход в насыщенное устойчивое состояние.

  С точки термодинамики можно различать идеаль­ные растворы и неидеальные (или реальные). В идеальных растворах, к которым реальные могут только приближаться, внутренняя энергия каждого компонента не зависит от концентрации. Компоненты в идеальном растворе смешиваются, как идеальные газы; предполагается, что сил взаимодействия между частицами нет, и вещества смешиваются без выде­ления или поглощения теплоты.

Растворы, не удовлетворяющие указанным условиям, относят к реальным растворам. Чем меньше концентрация раствора, тем ближе он к идеальному раствору. Растворы изотопов одного элемента в дру­гом почти точно подчиняются законам идеальных растворов. Одно­родные смеси неполярных веществ (углеводородов) близки к идеаль­ным растворам при всех концентрациях. Растворы полярных веществ, особенно электролитов, обнаруживают заметное отклонение от иде­альности уже при концентрациях, отвечающих мольной доле поряд­ка одной миллионной.

IV.Способы выражения состава растворов

Любой раствор состоит из растворителя и растворенного вещества. В случае растворов газов или твердых веществ в жидкостях растворителем обычно считается жидкость, а растворенным веществом – растворенный газ или твердое вещество, независимо от их относительного количественного содержания. Когда компоненты обладают ограниченной смешиваемостью, то растворителем является тот, прибавление которого к раствору возможно в неограниченном количестве без нарушения гомогенности. Если компоненты обладают неограниченной растворимостью, то можно выделить два случая. При значительном различии содержания компонентов растворителем считается вещество, присутствующее в относительно большем количестве. Понятия растворитель и растворенное вещество теряют смысл, когда речь идет о смесях с примерно равными или близкими концент­рациями компонентов. В этом случае состав раствора может выражаться различными способами – как с помощью безразмерных единиц – долей или процентов, так и через размерные величины – концентрации. На практике используют более десятка способов выражения концентрации. Вот некоторые из них:

1. Массовая доля растворенного вещества.

Отношение массы растворенного вещества B к массе растворителя.

или

1. Мольная доля растворенного вещества.

Отношение количества растворенного вещества к суммарному количеству всех веществ, составляющих раствор, включая растворитель

или

Мольная доля указывает на число молей данного вещества в одном моле раствора. Сумма мольных долей всех составных веществ равна единице:

1. Объемная доля растворенного вещества:

Отношение объема растворенного вещества к сумме объемов вещества и растворителя.

или

1. Молярная концентрация (или молярность).

Определяется отношением числа молей растворенного вещества к объему раствора, выраженному в литрах. Физический смысл молярной концентрации заключается в том, что она указывает на число молей вещества содержащегося в 1 литре его раствора.

1. Нормальная концентрация (или нормальность).

Определяется отношением числа эквивалентов растворенного вещества B к объему раствора, выраженному в литрах. Физический смысл нормальной концентрации заключается в том, что она указывает на число эквивалентов растворенного вещества, содержащегося в 1 литре раствора.

1. Моляльная концентрация (или моляльность).

Определяется отношением числа молей растворенного вещества к массе растворителя. Физический смысл заключается в том, что она показывает, сколько молей вещества растворено в 1 кг (1000г) растворителя.

Применение того или иного способа выражения концентрации зависит от решения конкретных практических задач.

V.Растворимость. Зависимость растворимости от температуры.

Р

.

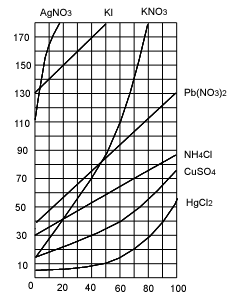
зависимость растворимости жидкостей от температуры

Растворение большинства твердых веществ в жидкостях сопровождается обычно поглощением энергии. Это объясняется затратой значительного количества энергии на разрушение кристаллической решетки твердого вещества. В этом случае растворимость твердых веществ увеличивается с ростом температуры. Но если растворение сопровождается выделением энергии, то растворимость с ростом температуры понижается. Такое явление наблюдается при растворении в воде щелочей, солей лития, магния, алюминия.

Т

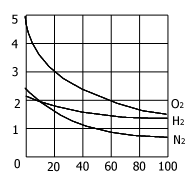
зависимость растворимости газов от температуры

На практике растворимость вещества выражается величиной, называемой коэффициентом растворимости. Коэффициент растворимости показывает массу вещества, насыщаемую при данной температуре 100 граммов растворителя.

Растворимость некоторых веществ в воде представлена в таблице

VI.Теплоты растворения и разбавления.

Изменение энтальпии при переходе твердого, жидкого или газообразного вещества в раствор называется теплотой или энтальпией растворения. Эндотермические реакции характеризуются положительным изменением энтальпии, а экзотермические – отрицательным. Энтальпией растворения называют изменение энтальпии при растворении 1 моль вещества в некотором количестве чистого растворителя. Процесс растворения в термохимии обычно выражают термохимическим уравнением, например процесс растворения a моль Pb(NO3)2 в b моль воды можно представить уравнением:

Теплота растворения зависит от концентрации полученного раствора и от температуры.

Особый интерес представляют первая и полная теплоты растворения. Первой теплотой растворения называется изменение энтальпии при растворении 1 моль вещества в бесконечно большом количестве растворителя. В результате этого процесса образуется бесконечно разбавленный раствор. Полной теплотой растворения называется изменение энтальпии при растворении 1 моль вещества в таком количестве чистого растворителя, которой необходимо для образования насыщенного раствора.

Тепловой эффект взаимодействия раствора данной концентрации с чистым растворителем называется энтальпией разведения или разбавления. Если раствор, содержащий 1 моль растворенного вещества, разбавляется от данной концентрации до определенной конечной (не бесконечно малой) концентрации, то тепловой эффект тепловой эффект называется промежуточной теплотой разбавления.

VII.Давление пара растворов. Состав пара растворов.

Давление насыщенного пара является весьма важным свойством растворов. С его величиной непосредственно связаны многие свойства растворов. Допустим, что к пару применимы законы идеальных газов. Воспользуемся упрощенной схемой испарения. Растворяя большое количество какого-либо вещества в данном растворителе, мы понижаем концентрацию молекул последнего в единице объема и уменьшаем этим число молекул, вылетающих в единицу времени из жидкой фазы в газообразную. В результате равновесие между жидкостью и паром устанавливается при меньшей концентрации раствора, т.е. при меньшем его давлении. Следовательно, давление насыщенного пара растворителя над раствором, должно быть всегда меньше, чем над чистым растворителем. При этом понижение давления пара будет, тем больше чем больше концентрация растворенного вещества в растворе. Из этого вытекает закон Генри, который можно выразить уравнением:

, где

p – парциальное давление

k – константа Генри

Закон Генри звучит так: Парциальное давление пара растворенного вещества пропорционально его концентрации в растворе.

При NA=1 парциальное давление пара pA представляет собой давление насыщенного данного компонента в свободном состоянии . Следовательно k= и равенство принимает вид:

Концентрация растворенного вещества в растворе при выражении ее в мольных долях этого вещества NA связана с концентрацией растворителя как

NA+ NB =1. Подставляя это выражение в закон Генри получим:



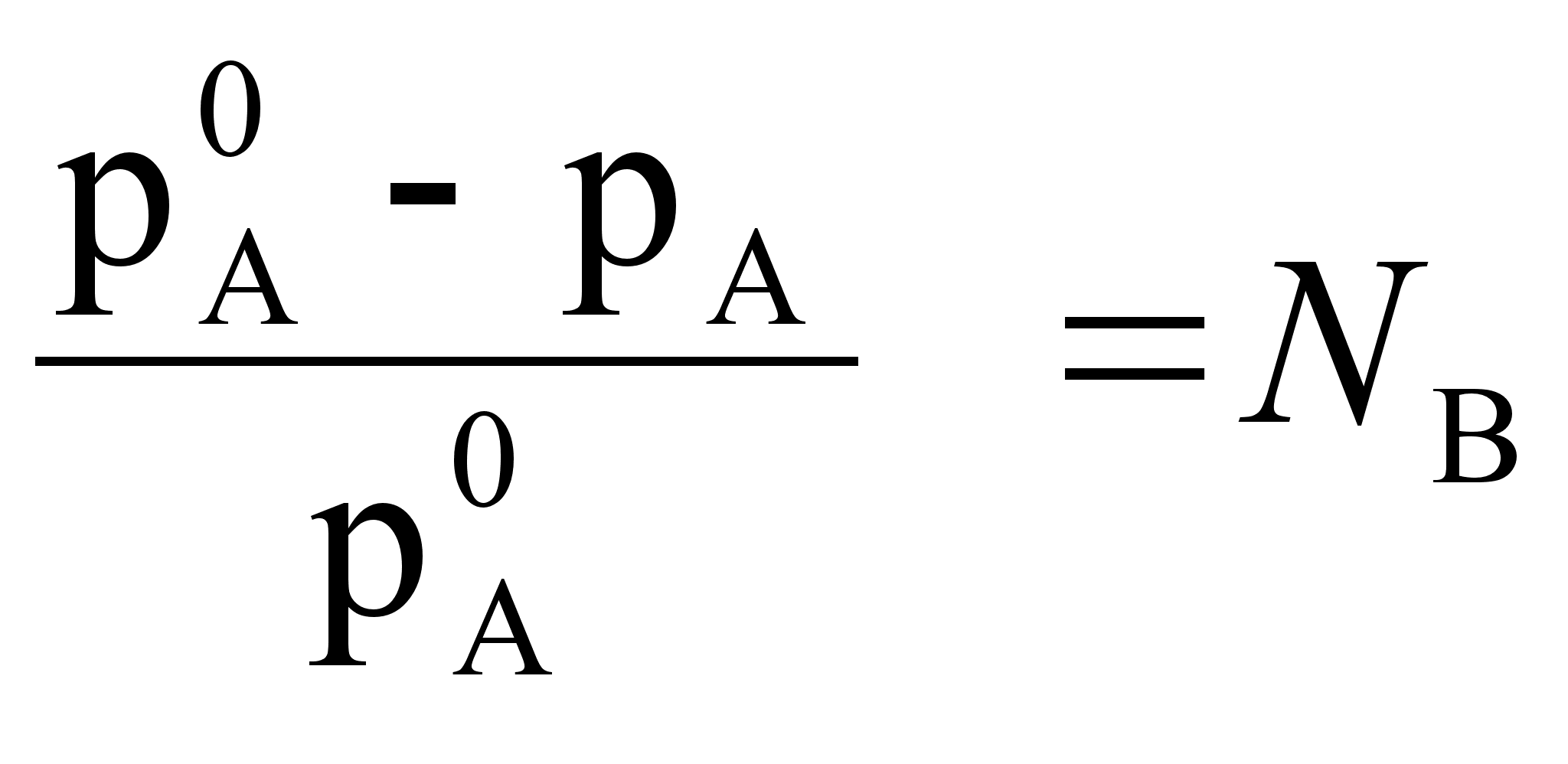
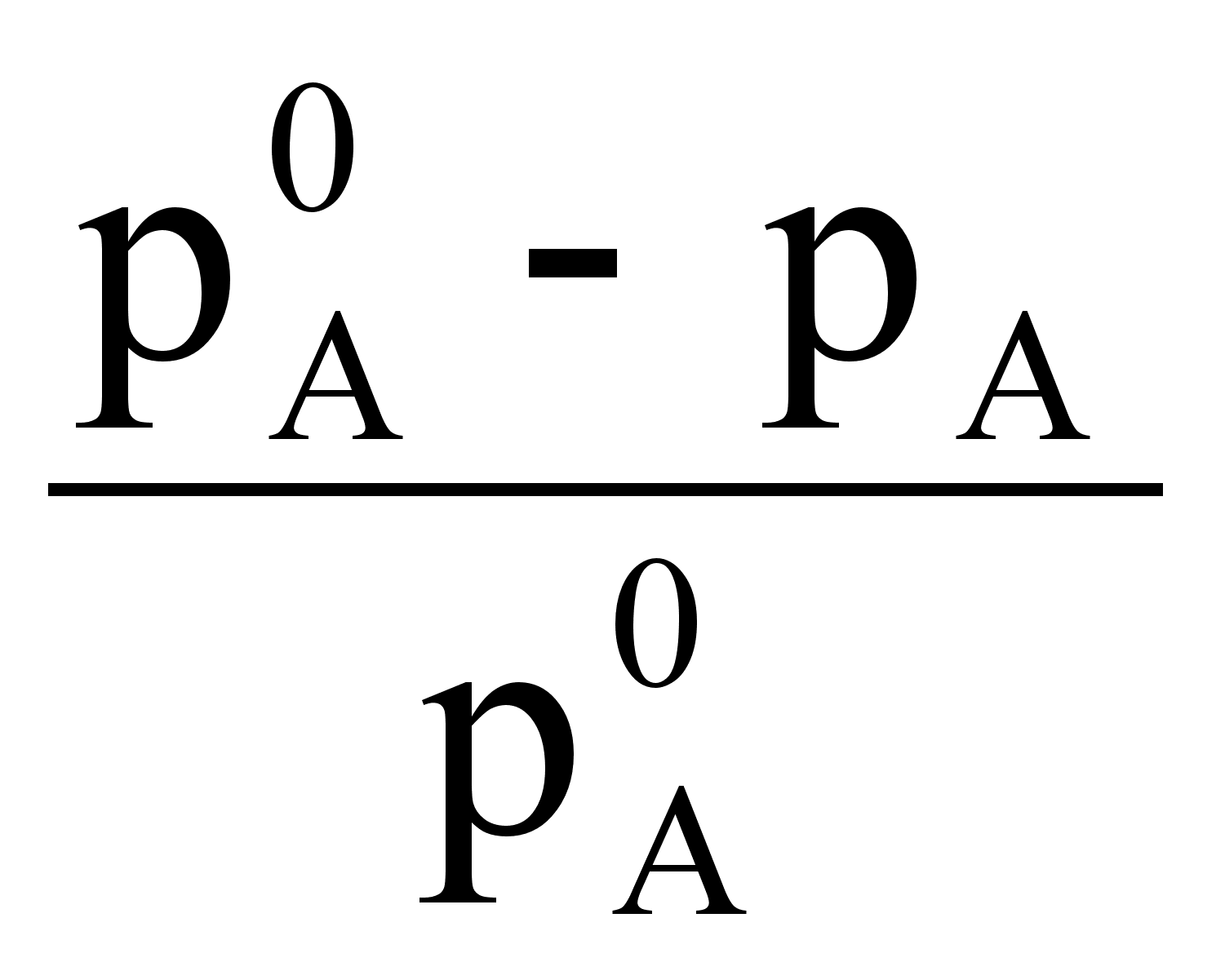Разность () называется понижением давления насыщенного пара, а отношение -относительным понижением давления насыщенного пара.

Согласно закону Рауля: Относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле вещества в растворе

Если графически изобразить зависимость давления пара каждого вещества двухкомпонентной смеси от его мольной доли, поучиться прямая линия. Пусть даны вещества А и В. Обозначим их мольные доли NA и NB. По закону Рауля имеем:

p
A=* NA, pB=* NВ

где p0 есть давление пара чистого вещества. Это суть уравнения прямых, если на осях отложены давления пара и мольные доли.

Для общего давления пара раствора отсюда следует равенство: p=* NA + * NВ

Эта линейная зависимость осложняется если между компонентами смеси действуют силы притяжения, и она изображается не прямой, а кривой линией

Если оба компонента раствора в чистом состоянии летучи, то пар будет содержать оба компо­нента. Однако относительное содержание компонентов в парах в общем случае будет отличаться от относительного содержания их в жидкостях. Для простейших систем легко установить соотношение между составами раствора и пара, равновесного с ним. Только b системе, компоненты которой обладают одинаковым давлением пара в чистом состоянии, состав пара над раствором равен составу раствора. В остальных же случаях состав пара отличен от состава рас­твора и тем в большей степени, чем больше различаются дав­ления пара над чистыми ком­понентами. В простейших си­стемах в парах всегда преоб­ладает по сравнению с жидко­стью тот из компонентов, кото­рый обладает большим давле­нием пара в чистом состоянии.

В количественной форме соотношения между составом пара и жидкости могут быть выведены следующим путем. Обозначим через NA’ и NB’ мольные доли компонентов в парах, причем NA’= и NB’=

Пользуясь законом Рауля легко получить, что p=, а пользуясь выражением p= получаем, что =

Для систем, в которых зависимость давления пара от состава нелинейная, нет общего выражения, в такой простей форме связы­вающего составы пара и раствора. Зависимость состава пара от состава раствора и общего давления характеризуется законом, открытым Д.И.Коноваловым и носящими его имя. Закон Коновалова характеризует соотношения между составами равновесных жидкостей и пара и влияние добавления того или иного компонента на общее давление пара. Он формулируется следующим образом:

а) Повышение относительного содержания компонента в жидкой фазе всегда вызывает увеличение относительного содержания его и в парах.

b) В двойной системе пар, по сравнению с находящейся с ним в равновесии жидкостью, относительно более богаче тем из компонентов, прибавление которого к системе повышает общее давление пара, т.е. понижает температуру кипения смеси при данном давлении.

Введем в раствор из двух веществ какое-либо новое вещество. В общем случае это вещество распределится между обоими веществами в растворе, пропорционально своей растворимости в каждом из них. Отсюда втекает закон распределения, согласно которому вещество, способное растворяться в двух несмешивающихся растворителях, распределяется между ними так, что отношение его концентраций в этих растворителях при постоянной температуре остается постоянным, независимо от общего количества растворенного вещества.

где С1B и С2B - концентрации растворенного вещества в первом и втором растворителях;

KD(B) – константа распределения вещества B между двумя жидкими несмешивающимися фазами.

VIII.Неидеальные растворы.

Реальные растворы в подавляющем большинстве не подчиняются законам идеальных растворов. Очень многие из них не подчиняются, например, закону Рауля, причем известны как положительные, так и отрицательные отклонения. Если давление пара над реальным раствором больше, чем над идеальным такого же состава, то отклонения от закона Рауля называют положительными, а если меньше, то отрицательными. Знак и величина отклонения зависит от природы растворителя и растворенного вещества. . Если молекулы одного компонента сильнее притягиваются друг к другу, чем к молекулам другого компонента, то парциальные давления пара над смесью будут больше вычисленных. Если же частицы разных компонентов притягиваются друг к другу сильнее, чем частицы одного и того же компонента, то парциальные давления будут меньше вычисленных.

В реальных растворах взаимодействия между однородными и разнородными молекулами различны. Если раствор образуется из частных компонентов А и В, то изменение потенциальной энергии при образовании раствора равно:



а) в)

Двукомпонентная система с

а)отрицательным отклонением от закона Рауля

в)положительным отклонением от закона Рауля

UA-A, UB-B и UA-B - средние потенциальные энергии взаимодействия между однородными и разнородными молекулами соответственно, если U=0, то раствор идеальный. Идеальные растворы при всех концентрациях и температурах подчиняются закону Рауля.

IX.Активность и коэффици­ент активности.

При рассмотрении термодинамических свойств растворов принято пользоваться отношением

Эта величина называется активностью i в растворе. Согласно уравнению отношение равно мольной концентрации данного компонента в растворе. Активность пред­ставляет собой вспомогательную расчетную термодинамическую функцию, которая характеризует степень свя­занности молекул компонента. При образовании данным компо­нентом в растворе каких-нибудь соединений его активность становится меньше и, наоборот, активность возрастает при уменьшении степени ассоциации компонента. Активность дает возможность су­дить об отклонении свойств данного компонента в том или ином растворе от свойств в простейшем растворе при той же мольной концентрации компонента. Активность зависит от вида и концен­трации каждого из других компонентов .раствора. Она зависит также от температуры и от давления, но не зависит от способа выражения концентрации. Химический потенциал данного компонента в растворе связы­вается с активностью соотношением:

Вместо активности нередко пользуются величиной коэффи­циента активности, . Он равен отношению активности к концен­трации =. Коэффициент активности характеризует степень отклонения свойств рассматри­ваемого компонента в данном растворе от его свойств в соответствующем простейшем растворе. В сильно разбавленном растворе коэффициент активности равен единице. Чем более концентрирован раствор, тем больше отличается активность от концентрации.

X.Кристаллизация растворов.

Раствор, в отличие от чистой жидкости не отвердевает целиком при одной температуре. Кристаллы начинают выделяться при какой-то одной температуре. По мере понижения температуры количество их растет, пока весь раствор не отвердеет. Температурой начала кристаллизации называют температуру, при которой при охлаждении раствора начинается образование кристаллов. Не рассматривая здесь систем, в которых происходит образование твердых растворов, можно сказать, что температурой начала кристаллизации называется температура, при которой кристаллы растворителя находятся в равновесии с раствором данного вещества. Опыт показывает, что разбавленный раствор замерзает при температуре более низкой, чем чистый растворитель. Такое изменение температуры можно рассматривать как общее правило. Для характеристики температуры замерзания раствора введена величина “понижение температуры замерзания” T 3. Она определена как разность между температурами замерзания чистого растворителя и раствора:

T3=.

Понижение температуры замерзания пропорционально концентрации растворенного вещества в растворе.

T=K*c

Коэффициент K называется молярным понижением температуры замерзания или криоскопической постоянной. К = , где

-температура замерзания растворителя

lпл – удельная теплота плавления

XI.Кипение растворов.

Если рассматривать растворы нелетучего вещества в летучих растворителях, то температура кипения таких растворов всегда выше температуры кипения чистого растворителя. Повышение температуры кипения будет тем больше, чем выше концентрация раствора. И для разбавленных растворов его можно считать пропорциональным концентрации. Для растворов температуры кипения являются более высокими, чем для чистого растворителя и разность между ними

Ткип = T кип -

будет тем большей, чем выше концентрация растворов. Повышение температуры кипения пропорционально концентрации раствора.

T кип = Е*с

Коэффициент пропорциональности Е является постоянной. Он называется молярным повышение температуры кипения или эбуллиоскопической постоянной. Е = , где - температура кипения чистого растворителя

lисп – удельная теплота его испарения

XII.Осмос.

Раствор представляет собой гомогенную систему. Все частицы растворенного

вещества находятся в беспорядочном тепловом движении равномерно распределены по всему объему раствора.

Если поместить в сосуд концентрированный раствор какого-либо вещества, например, сахара, а поверх его осторожно налить слой более разбавленного раствора сахара, то вначале сахар и вода будут распределены в объеме раствора неравномерно. Но через некоторое время молекулы сахара и воды вновь равномерно распределяться по всему объему жидкости. Это происходит потому, что молекулы сахара, беспорядочно двигаясь проникают как из концентрированного раствора в разбавленный, и в обратном направлении, но при этом в течение любого промежутка времени из концентрированного раствора переходит в разбавленный раствор больше молекул, чем из разбавленного в концентрированный. Точно так же ведут себя и молекулы воды. Таким образом возникает направленное движение молекул сахара из концентрированного раствора в разбавленный, а воды – из разбавленного раствора в концентрированный. Такой самопроизвольный процесс перемещения вещества, приводящий к выравниванию его концентрации, называется диффузией. Когда концентрация раствора во всем его объеме выравнивается, диффузия прекращается. В рассмотренном случае частицы растворителя и растворенного вещества диффундируют в противоположных направлениях. Такой процесс называется двусторонней или встречной диффузией. Но возможен и другой случай, когда между веществами поместить перегородку, через которую растворитель проходить может, а растворенное вещество нет. Односторонняя диффузия вещества через такую перегородку называется осмосом.

Возьмем два сосуда, расположенные один в другом . Пусть дно внутреннего сосуда сделано из полунепроницаемого материала. Наружный сосуд наполним водой, а во внутренний поместим водный раствор, например сахара в воде. Рассмотрим процесс, происходящий в приборе, состоящем из этих двух сосудов. Из наружного сосуда вода будет проходить во внутренний и подниматься по трубке, соединенной с внутренним сосудом. При этом повышается гидростатическое давление, под которым находится раствор во внутреннем сосуде. Наконец при некоторой высоте столба жидкости ее подъем прекратиться. Давление, которое отвечает такому равновесию может служить количественной характеристикой осмоса и называется осмотическим давлением. Таким образом осмотическое давление равно тому давлению, которое нужно приложить к раствору, чтобы привести его в равновесие с чистым растворителем, отделенным от него полунепроницаемой перегородкой. Описанный метод дает возможность измерять осмотическое давление. Опытные данные позволяют установить, что в достаточно разбавленных растворах осмотическое давление  прямо пропорционально концентрации растворенного вещества:

=KС

Сравнение осмотического давления одних и тех же растворов при разных температурах приводит к выводу, что осмотическое давление изменяется прямопропорционально абсолютной температуре.

=СRT,

где R – универсальная газовая постоянная.

Это уравнение по форме совпадает с уравнением состояния идеального газа, так как связь между концентрацией и объемом выражается, как С=.Таким образом осмотическое давление равно тому газовому давлению, которым обладало растворенное вещество, если бы, находясь в газообразном состоянии при той же температуре, оно занимало бы весь объем, который занимает раствор. Этот закон называется законом Вант-Гоффа

Список литературы

1. В.А. Киреев “Курс физической химии”,М. 1975

2. Н.Л.Глинка “Общая химия”, М. 2000

3. М.К.Дей, Д.Селбин “Теоретическая неорганическая химия”, М. 1971

4. Л.А.Николаев “Общая и неорганическая химия” М. 1974

5. К.С.Краснов “Физическая химия” М. 2001